Câu 1: (1,5 điểm)

Cho biểu thức

a) Rút gọn biểu thức A.

b) Tìm các giá trị nguyên của x để A nguyên.

Câu 2: (2,0 điểm)

a) Giải phương trình:

b) Giải hệ phương trình: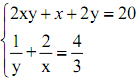

Câu 3: (1,5 điểm)

Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): 2x – y – a² = 0 và Parabol (P): y = ax² (a là tham số dương)

a) Tìm giá trị a để (d) cắt (P) tại hai điểm phân biệt A, B. Chứng tỏ khi đó A và B nằm bên phải trục tung.

b) Gọi x₁; x₂ lần lượt là hoành độ của A và B. Tìm giá trị nhỏ nhất của

Câu 4: (2,0 điểm)

Cho tam giác nhọn ABC có góc đỉnh A là 45^o. Nửa đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại E và F. Vẽ bán kính OM vuông góc với BC.

a) Chứng minh EF = R√2 (Với BC = 2R).

b) Chứng minh M là trực tâm tam giác AEF.

Câu 5. (2,0 điểm)

Cho tam giác nhọn ABC nội tiếp đường tròn (O), có AB < AC. Hạ các đường cao BE và CF, gọi H là trực tâm, M là giao điểm của EF và AH. Vẽ đường kính AK cắt cạnh BC tại N.

a) Chứng minh ΔAMF đồng dạng với tam giác ΔANC.

b) Chứng minh HI song song với MN, với I là trung điểm BC.

Câu 6. (1 điểm)

Cho hai số x, y thỏa mãn:

Tìm giá trị lớn nhất và nhỏ nhất của tích xy.

Download tài liệu để xem thêm chi tiết.