Câu 1.

Cho dãy số (u_n) thỏa mãn u₁ = 1 và ; trong đó a ≥ 0. Tìm a sao cho (u_n) hội tụ và tìm giới hạn đó.

Câu 2.

Cho hai hàm f(x) và g(x) xác định trên R và thỏa mãn điều kiện (f(x) − f(y))(g(x) − g(y)) = 0 với mọi x; y ∈ R.

Chứng minh ít nhất một trong hai hàm f hoặc g là hàm hằng.

Câu 3.

1) Cho hàm số f đơn điệu trên [0;∞) và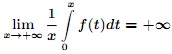

Chứng minh rằng:

2) Kết luận trên còn đúng không khi f là hàm liên tục trên [0;∞) nhưng không đơn điệu trên khoảng đó? Tại sao?

Câu 4.

Tìm tất cả các hàm số f(x) xác định, liên tục trên đoạn [0; 1], khả vi trong khoảng (0; 1) và thỏa mãn điều kiện:

Câu 5.

Cho dãy số (x_n) được xác định bởi

Tìm với điều kiện x₀ ≥ 4; x₁ ≥ 4.

Câu 6. Thí sinh chọn một trong hai câu:

6a. Cho (a_n) là dãy số xác định bởi

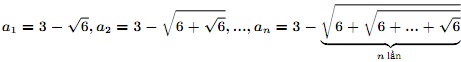
Hãy chứng minh rằng chuỗi số hội tụ.

6b. Cho f là hàm số liên tục trên [0;+∞). Giả sử rằng

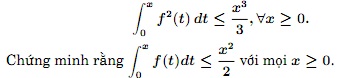
Download tài liệu để xem chi tiết.