Bài 1 (4 điểm):

Giải hệ phương trình sau: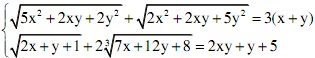

Bài 2 (4 điểm):

Cho đường tròn (O) đường kính AB, C là điểm di động trên (O) không trùng với A và B. Các tiếp tuyến của (O) tại B và C cắt nhau tại N, AN cắt (O) tại D khác A. Tiếp tuyến của (O) tại D cắt CN tại P. Chứng minh rằng P di động trên một đường cố định khi C di động trên (O).

Bài 3 (3 điểm):

Cho a, b, c là ba số thực dương tùy ý. Chứng minh:

Bài 4 (3 điểm):

Tìm tất cả các số nguyên dương k sao cho phương trình: x² + y² + x + y = kxy có nghiệm nguyên dương x , y.

Bài 5 (3 điểm):

Cho trước số nguyên dương n ≥ 2. Trong một giải đấu cờ vua có 2n vận động viên tham gia, mỗi người đấu với người khác đúng một ván. Tại một thời điểm trong giải, người ta thấy có n² + 1 ván đấu đã diễn ra. Chứng minh rằng khi đó có thể chọn ra ba vận động viên sao cho hai người bất kỳ trong ba người được chọn đều đã thi đấu với nhau.

Bài 6 (3 điểm)

Cho hàm số f: N* → N*\{1} (N* là tập hợp các số nguyên dương) thỏa mãn: f(n) + f(n + 1) = f(n + 2)f(n + 3) – 168.

Tính f(2014).

Download tài liệu để xem chi tiết.