Câu 1 (4 điểm):

Giải hệ phương trình: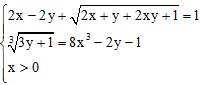

Câu 2 (4 điểm):

Cho dãy:

a) Chứng minh dãy (a_n) hội tụ và tính lima_n

b) Chứng minh

Câu 3 (4 điểm):

Gọi AD, BE, CF là ba đường phân giác trong của tam giác ABC vuông ở A. Đoạn thẳng AD cắt EF tại K. Đường thẳng qua K song song với BC cắt AB, AC lần lượt ở M, N. Chứng minh rằng:

Câu 4 (4 điểm):

Tìm tất cả các hàm số f: R → R thoả mãn: f(x² + y²) = xf(x) + yf(y), với mọi x, y thuộc R (1)

Câu 5 (4 điểm):

Cho 100 số tự nhiên không lớn hơn 100 có tổng bằng 200. Chứng minh rằng từ các số đó có thể chọn được ít nhất một bộ các số có tổng bằng 100.

Download tài liệu để xem chi tiết.