Trang chủ
Đề thi & kiểm tra
Lớp 7
Toán học
Giải SBT Toán 7 Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án !!
Giải SBT Toán 7 Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp...
Câu hỏi 1 :
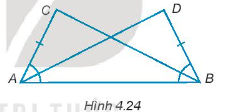
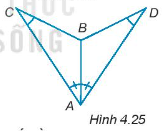
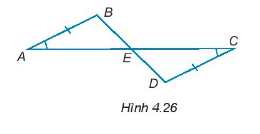
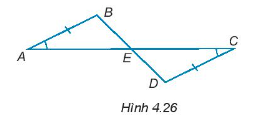
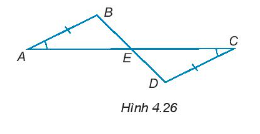
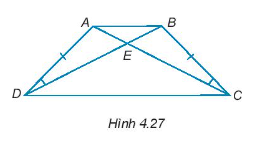
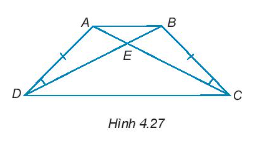
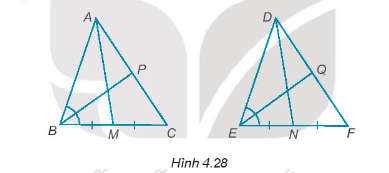
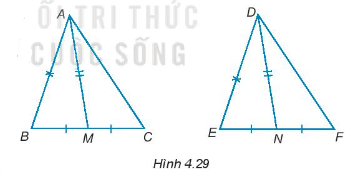
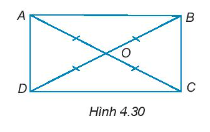
Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
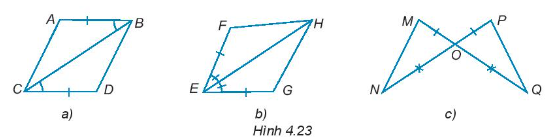
Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK