Trắc nghiệm Toán 7 Bài 4. Định lí có đáp án !!
Câu hỏi 1 :
Định lí thường được phát biểu dưới dạng:
A. Thì … là…;
B. Nếu … thì …;
C. Vì … nên …;
D. Do … nên ….
Câu hỏi 2 :
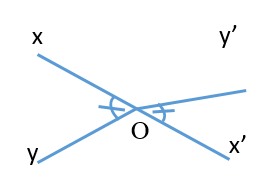
Phát biểu định lý sau thành lời:
A. Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau;
B. Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau;
C. Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau;
D. Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng vuông góc với nhau.
Câu hỏi 3 :
Định lí: “Nếu hai đường thẳng song song cùng cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau”. Giả thiết của định lí là:
A. a // b; a // c;
B. a // c; b bất kì;
C. a // b; \[a \bot c\];
D. \[a//b;\;c\, \cap \,a = \left\{ M \right\};\;c\, \cap b = \left\{ N \right\}\].
Câu hỏi 4 :
Chọn phát biểu đúng
A. Giả thiết của định lí là điều suy ra;
B. Kết luận của định lí là điều cho biết;
C. Giả thiết của định lí là điều cho biết;
D. Cả A và B đều đúng.
Câu hỏi 5 :
Điền vào chỗ trống những nội dung thích hợp để được định lí đúng.
A. N thuộc AB;
B. N là trung điểm của AB;
C. N nằm giữa AB;
D. Cả 3 đáp án trên đều sai.
Câu hỏi 6 :
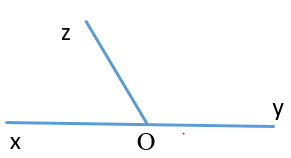
Điền vào chỗ trống nội dung thích hợp.
A. a, b song song với nhau;
B. a, b vuông góc với nhau;
C. a, b cắt nhau;
D. a, b trùng nhau.
Câu hỏi 7 :
Điền vào chỗ trống: “Nếu một đường thẳng cắt hai đường thẳng song song thì …”
A. Hai góc đồng vị bằng nhau;
B. Hai góc so le trong bằng nhau;
C. Hai góc kề bù bằng nhau;
D. Cả A và B đều đúng.
Câu hỏi 8 :
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
A. 
B. 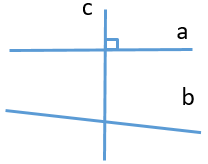
C. 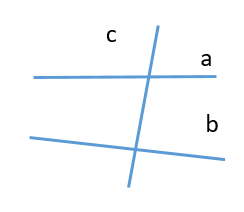
D. 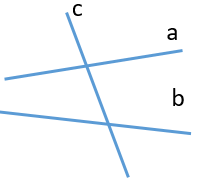
Câu hỏi 9 :
Viết giả thiết cho định lí sau:
A. Giả thiết: a ≠ b; a // c, b // c;
B. Giả thiết: a ≡ b; a // b, b // c;
C. Giả thiết: \[a \equiv b;\;a\, \bot c,\;b\,//c\];
D. Giả thiết: \[a \ne b;\;a\, \bot c,\;b\,//c\].
Câu hỏi 10 :
Điền vào chỗ trống.
A. hai góc đó có tổng số đo bằng 180°;
B. hai góc đó không bằng nhau;
C. hai góc đó bằng nhau;
D. hai góc đó có hiệu số đo bằng 180°.
Câu hỏi 11 :
Trong định lí, phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết vậy phần nằm sau từ “thì” là phần?
A. kết luận;
B. trả lời;
C. ý nghĩa;
D. định nghĩa.
Câu hỏi 12 :
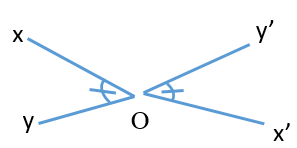
Phát biểu định lí sau bằng lời.
A. Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng a, b vuông góc với nhau;
B. Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng a, b song song với nhau;
C. Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau;
D. Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b vuông góc với nhau.
Câu hỏi 14 :
Viết giả thiết, kết luận cho định lí sau:
A.
Giả thiết | c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc so le trong \[\widehat {{A_3}} = \widehat {{B_1}}\] |
Kết luận | a // b |
B.
Giả thiết | c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đồng vị \[\widehat {{A_3}} = \widehat {{B_1}}\] |
Kết luận | a // b |
C.
Giả thiết | c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc so le trong \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
Kết luận | a // b |
D.
Giả thiết | c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đồng vị \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
Kết luận | a // b |
Câu hỏi 15 :
Chứng minh định lí là:
A. Dùng lập luận để từ giả thiết suy ra kết luận;
B. Dùng hình vẽ để từ giả thiết suy ra kết luận;
C. Dùng đo đạc thực tế để từ giả thiết suy ra kết luận;
D. Cả 3 đáp án đều đúng.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAPSGK

 .
.