Hình học 12 Bài 1: Khái niệm về mặt tròn xoay

a) Mặt nón

Trong không gian cho hai đường thẳng \(\Delta\) và \(l\) cắt nhau tại O sao cho \((\widehat{\Delta ,l})=\alpha \, (0^{\circ}< \alpha < 90^{\circ}).\)
Cho \(l\) quay quanh \(\Delta\) ta được mặt nón tròn xoay có:

• là đường sinh.
• \(\Delta\) trục của mặt nón.
• \(O=l\cap \Delta\) đỉnh của mặt nón.
• \(2\alpha :\) góc ở đỉnh.

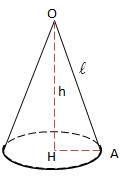
b) Hình nón

Cắt mặt nón tròn xoay đỉnh O, trục \(\Delta\) bởi mặt phẳng (P) sao cho \((P)\perp \Delta ,O\notin (P).\) 

Hình giới hạn bởi mặt nón, mặt phẳng (P) được gọi là hình nón.

c) Khối nón

Khối nón tròn xoay là phần không gian giới hạn bởi hình nón tròn xoay kể cả hình nón đó.

d) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:

• Thể tích khối nón: \(V_{Khoi \, \, non}=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).
• Diện tích xung quanh hình nón: \(S_{xq}=\pi Rl\).
• Diện tích toàn phần hình nón: \(S_{tp}=\pi Rl+\pi R^{2}\).

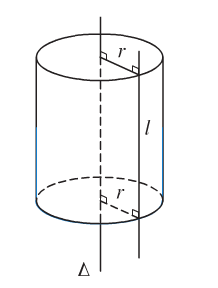
a) Mặt trụ

Trong không gian, cho đường thẳng \(l\) song song và cách đường thẳng \(\Delta\) một khoảng R.

Cho \(l\) quay quanh \(\Delta\) ta được một mặt tròn xoay được gọi là mặt trụ tròn xoay có:

• \(l\) là đường sinh.
• \(\Delta\) là trục mặt trụ.
• R là bán kính mặt trụ.

b) Hình trụ

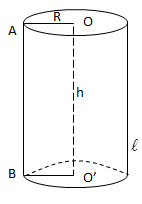
Xét hình chữ nhật OABO'.

Cho đường gấp khúc OABO' quay quanh OO' ta được hình trụ tròn xoay:

• OA: Bán kính đường tròn đáy.
• AB: đường sinh.

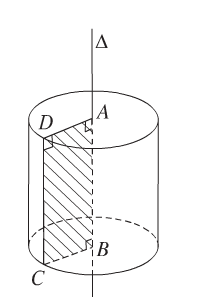
c) Khối trụ

Khối trụ tròn xoay là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ đó.

d) Các công thức tính toán liên quan đển hình trụ, khối trụ

• Thể tích khối trụ: \(V=\pi .R^2.h\) (=Sđáy.h).
• Diện tích xung quanh hình trụ: \(S_{xq}=2\pi .R.h\).
• Diện tích toàn phân hình trụ: \(S_{tp}=2\pi .R.h+2\pi R^2\).
  • Trong đó:
    • R: bán kính đáy.
    • h: chiều cao (k/c giữa hai đáy = OO').​

1. Bài tập liên quan đến mặt nón - hình nón -khối nón

Ví dụ 1: 

Trong không gian cho tam giác ABC vuông tại A có AB=a, AC = 2a. Quay tam giác ABC xung quanh cạnh AB ta được một khối nón. Tính thể tích V của khối nón đó.

Lời giải: 

Hình nón thu được có bán kính đáy R=AC=2a, chiều cao h=AB=a.

Vậy thể tích khối nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{{4\pi {a^3}}}{3}.\)

Ví dụ 2:

Trong không gian cho tam giác ABC vuông tại A có có AB=5, AC=12. Cho đường gấp khúc BAC quay quanh cạnh BC ta được hình nón tròn xoay. Tính thể tích của khối nón đó.

Lời giải:

Khi quay đường gấp khúc BAC quay quanh cạnh BC ta được hai hình nón:

Hình nón thứ nhất có đường cao \({h_1} = BH\), Bán kính đáy \({R_1} = AH\).

Hình nón thứ hau có đường cao \({h_2} = CH\), Bán kính đáy \({R_2} = AH\).

Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{{60}}{{13}}\)

\(BC = \sqrt {A{B^2} + A{C^2}} = 13\)

Vậy thể tích khối tròn xoay thu được là: \(V = \frac{1}{3}\pi {R_1}^2{h_1} + \frac{1}{3}\pi R_2^2{h_2} = \frac{1}{3}\pi A{H^2}(BH + CH) = \frac{{1200}}{{13}}\pi .\)

Ví dụ 3: 

Thiết diện qua trục của một hình nón là một tam giác vuông có cạnh góc vuông bằng a.

a) Tính diện tích xung quanh và diện tích toàn phần của hình nón.

b) Tính thể tích của khối nó.

c) Một thiết diện qua đỉnh tạo với đáy một góc 60⁰. Tính diện tích của thiết diện này.

Lời giải:

a) Thiết diện qua trục là tam giác SAB vuông cân tại S nên: \(\widehat A = \widehat B = {45^0}.\)

Diện tích xung quanh hình nón là: \({S_{xq}} = \pi Rl = \pi .OA.SA = \pi .\frac{a}{{\sqrt 2 }}.a = \frac{{\pi {a^2}}}{{\sqrt 2 }}.\)

Diện tích toàn phần hình nón là: \({S_{tp}} = {S_{xq}} + {S_{day}} = \frac{{\pi {a^2}}}{{\sqrt 2 }} + \frac{{\pi {a^2}}}{2} = \left( {\frac{1}{{\sqrt 2 }} + \frac{1}{2}} \right)\pi {a^2}.\)

b) Thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .O{A^2}.SO = \frac{1}{3}\pi .\frac{{{a^2}}}{2}.\frac{a}{{\sqrt 2 }} = \frac{{\pi {a^3}}}{{6\sqrt 2 }}.\)

c) Thiết diện (SAC) qua đỉnh tạo với đáy một góc 60⁰.

Kẻ \(OM \bot AC \Rightarrow SM \bot AC \Rightarrow \widehat {SMO} = {60^0}.\)

Do tam giác SMO vuông tại O nên \(OM = \frac{{SO}}{{\tan 60}} = \frac{{a\sqrt 6 }}{6}.\)

Tam giác OAM vuông tại M nên: \(AM = \sqrt {O{A^2} - O{M^2}} = \frac{{a\sqrt 3 }}{3}\).

Tam giác ABC vuông tại C (nội tiếp đường tròn) suy ra \(BC \bot AC.\)

Suy ra OM là đường trung bình của tam giác ABC.

Nên \(AC = 2AM = \frac{{2a\sqrt 3 }}{3}.\)   

Ta có: \(SM = SO.\sin {60^0} = \frac{{a\sqrt 6 }}{3}.\)

Vậy diện tích thiết diện là: \({S_{SAC}} = \frac{1}{2}.SM.AC = \frac{1}{2}.\frac{{a\sqrt 6 }}{3}.\frac{{2a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 2 }}{3}.\)

2. Bài tập liên quan đến mặt trụ - hình trụ - khối trụ

Ví dụ 4: 

Cho hình chữ nhật ABCD có AB = 2AD. Gọi V₁ là thể tích khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AB và V₂ là thể tích khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AD. Tính tỉ số \(\frac{V_2}{V_1}\).

Lời giải:

Khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AB có bán kính đáy AD, chiều cao AB: \({V_1} = AB.\left( {\pi A{D^2}} \right)\)

Khối trụ sinh ra do hình chữ nhật ABCD quay quanh đường thẳng AD có bán kính đáy AB, chiều cao AD: \({V_2} = AD.\left( {\pi A{B^2}} \right)\)

Vậy: \(\frac{{{V_2}}}{{{V_1}}} = \frac{{AD.\left( {\pi A{B^2}} \right)}}{{AB.\left( {\pi A{D^2}} \right)}} = \frac{{AB}}{{AD}} = 2.\)

Ví dụ 5:

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính diện tích xung quanh S của hình trụ tròn xoay ngoại tiếp lăng trụ.

Lời giải:

Diện tích xung quanh mặt trụ được tính theo công thức \({S_{xq}} = 2\pi .R.l\).

Gọi R là bán kính đường tròn ngoại tiếp \(\Delta ABC\).

\(\Rightarrow R = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\); \(l =AA'=a\).

Vậy diện tích cần tìm là \({S_{xq}} = 2\pi .\frac{{a\sqrt 3 }}{3}.a = 2\pi \frac{{{a^2}\sqrt 3 }}{3}\) (đvdt).

Ví dụ 6:

Một hình trụ có bán kính đáy R=5 cm và khoảng cách giữa hai đáy bằng 7 cm.

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.

b) Tính thể tích của khối trụ

c) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trụ 3cm. Hãy tính diện tích của thiết diện được tạo nên.

Lời giải:

Hình trụ có bán kính đáy R=5 và chiều cao h=7.

a) Diện tích xung quanh hình trụ là: \({S_{xq}} = 2\pi Rl = 2\pi .5.7 = 70\pi \,\,(c{m^2})\)

Diện tích toàn phần hình trụ là: \({S_{tp}} = {S_{xq}} + 2.{S_{day}} = 70\pi + 2\pi {.5^2} = 120\pi \,\,(c{m^2}).\)

b) Thể tích khối trụ là: \(V = \pi {R^2}h = \pi {.5^2}.7 = 175\pi \,\,(c{m^3}).\)

c) Gọi I là trung điểm của AB suy ra OI=3cm.

\(IB = \sqrt {O{B^2} - O{I^2}} = \sqrt {{5^2} - {3^2}} = 4.\)

Ta có: AB=2IB=8.

Dễ thấy thiết diện ABB'A' là hình chữ nhật.

Vậy diện tích thiết diện là: \({S_{ABB'A'}} = AB.AA' = 8.7 = 56\,\,(c{m^2}).\)

 

Nội dung bài học sẽ giới thiệu đến các em sự tạo thành hai mặt tròn xoay phổ biến là mặt nón và mặt trụ, các khái niệm hình nón, khối nón, hình trụ, khối trụ và các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của những vật thể tròn xoay dạng khối nón và khối trụ.

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 12 Chương 2 Bài 1 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Khẳng định nào sau đây là sai? 

  • A. Thể tích khối cầu có bán kính R: \(V = \frac{4}{3}\pi {R^3}\).
  • B.  Diện tích mặt cầu có bán kính R: \(S = 4\pi {R^2}\).
  • C. Thể tích của khối trụ có bán kính đáy R và chiều cao h là:  \(V = \pi {R^2}h\).
  • D. Thể tích của khối nón có bán kính đáy R và chiều cao h là:  \(V = \frac{1}{3}{\pi ^2}{R^2}h\).

• Câu 2:

  Một khối nón tròn xoay có độ dài đường sinh l = 13 cm và bán kính đáy r=5 cm. Tính thể tích V của khối nón.

  • A.  \(V = 100\pi \,\,c{m^3}\)
  • B.  \(V = 300\pi \,\,c{m^3}\)
  • C.  \(V = \frac{325}{3}\pi \,\,c{m^3}\)
  • D.  \(V = 20\pi \,\,c{m^3}\)

• Câu 3:

  Một tam giác ABC vuông tại A có AB = 6, AC = 8. Cho đường gấp khúc ABC quay quanh cạnh AC được hình nón có diện tích xung quanh và diện tích toàn phần lần lượt là S₁, S₂. Hãy chọn kết quả đúng.

  • A.  \(\frac{{{S_1}}}{{{S_2}}} = \frac{8}{5}\)
  • B.  \(\frac{{{S_1}}}{{{S_2}}} = \frac{5}{8}\)
  • C.  \(\frac{{{S_1}}}{{{S_2}}} = \frac{5}{9}\)
  • D.  \(\frac{{{S_1}}}{{{S_2}}} = \frac{9}{5}\)

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 12 Chương 2 Bài 1 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Hình học 12 Cơ bản và Nâng cao.

Bài tập 11 trang 53 SGK Hình học 12 NC

Bài tập 12 trang 53 SGK Hình học 12 NC

Bài tập 13 trang 53 SGK Hình học 12 NC

Bài tập 14 trang 53 SGK Hình học 12 NC

Bài tập 15 trang 53 SGK Hình học 12 NC

Bài tập 16 trang 54 SGK Hình học 12 NC

Bài tập 17 trang 59 SGK Hình học 12 NC

Bài tập 18 trang 59 SGK Hình học 12 NC

Bài tập 19 trang 60 SGK Hình học 12 NC

Bài tập 19 trang 60 SGK Hình học 12 NC

Bài tập 20 trang 60 SGK Hình học 12 NC

Bài tập 21 trang 60 SGK Hình học 12 NC

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.