Hình học 9 Bài 3: Góc nội tiếp
Tóm tắt bài
1.1. Định nghĩa
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong góc được gọi là cung bị chắn.
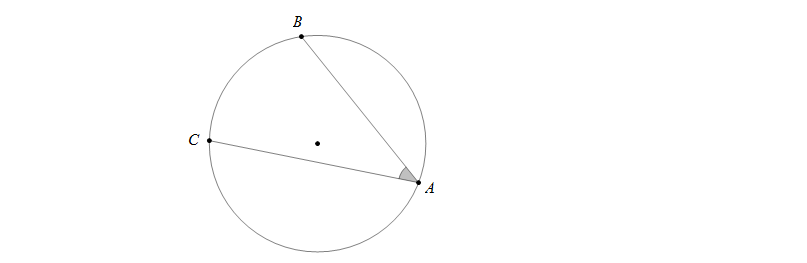
Góc \(\widehat{BAC}\) được gọi là góc nội tiếp, cung bị chắn là cung \(BC\)
1.2. Định lí
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
VD: Ở hình trên, góc nội tiếp \(\widehat{BAC}\) bằng nửa số đo cung bị chắn \(BC\), tức là \(\widehat{BAC}=\frac {1}{2}\)sđ\(\stackrel\frown{BC}\)
1.3. Hệ quả
Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau
c) Góc nội tiếp (nhỏ hơn hoặc bằng 900) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung
d) Góc nội tiếp chắn nửa đường tròn là góc vuông
2.1. Bài tập cơ bản
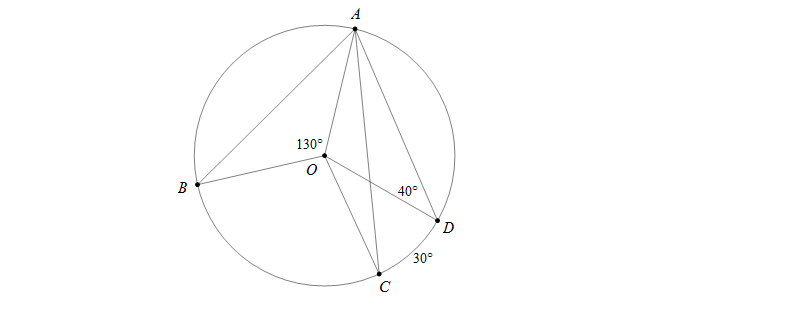
Bài 1: Dựa vào hình vẽ, hãy tính số đo cung \(BD\) nhỏ
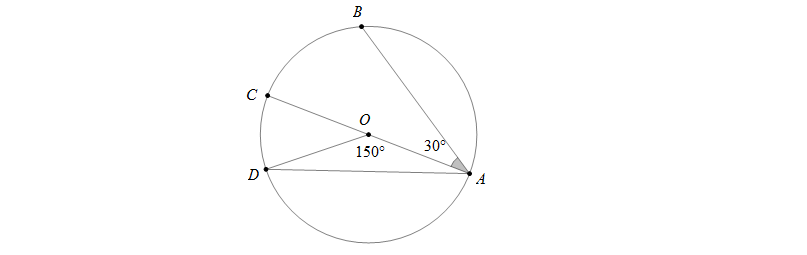
Hướng dẫn: \(\bigtriangleup OAD\) cân tại \(O\) nên \(\widehat{OAD}=\frac{180^0-150^0}{2}=15^0\), suy ra \(\widehat{BAD}=30^0+15^0=45^0\)
Mà \(\widehat{BAD}\) là góc nội tiếp nên sđ\(\stackrel\frown{BD}=2.\widehat{BAD}=2.45^0=90^0\)
Bài 2: Tính \(\widehat{MON}\) biết số đo cung nhỏ XY của đường tròn tâm B là 700
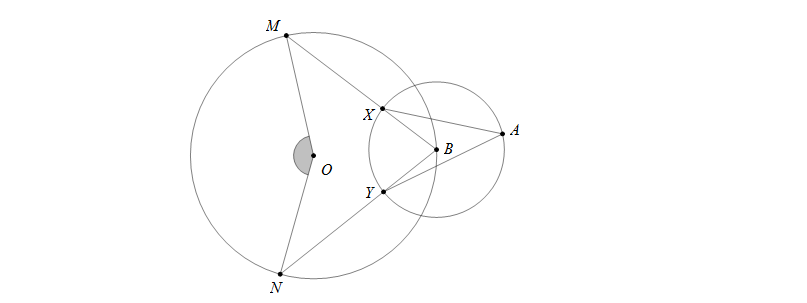
Hướng dẫn: Trong đường tròn \((B)\) ta có sđ\(\stackrel\frown{XY}=70^0\Rightarrow \widehat{XBY}=70^0\)
Trong đường tròn \((O)\) thì \(\widehat{MON}=2.\widehat{MBN}=2.70^0=140^0\)
Bài 3: Cho đường tròn \((O)\) và dây \(AB\). Vẽ \(OH\perp AB(H\in AB)\), \(OH\) cắt cung nhỏ \(AB\) tại \(N\). Biết rằng \(HN=5,AB=10\sqrt{5}\). Tính bán kính của đường tròn \((O)\)
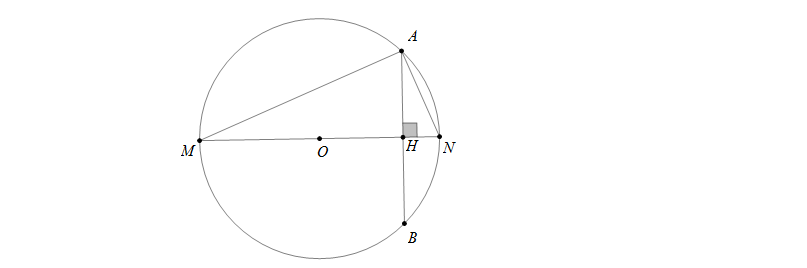
Hướng dẫn: Vẽ đường kính \(NOM\). Dễ chứng minh \(H\) là trung điểm của \(AB\) nên \(AH=\frac{1}{2}.AB=\frac{1}{2}.10\sqrt{5}=5\sqrt{5}\)
Áp dụng hệ thức lượng cho tam giác vuông MAN với đường cao AH ta có \(MH.HN=AH^2\Rightarrow MH=\frac{AH^2}{NH}=\frac{(5\sqrt{5})^2}{5}=25\)
Khi đó \(MN=MH+HN=25+5=30\)
Bán kính của đường tròn \((O)\) là \(ON=\frac{MN}{2}=15\)
2.2. Bài tập nâng cao
Bài 1: Cho đường tròn \((O;R)\) đường kính \(BC\) cố định. Điểm \(A\) di động trên đường tròn khác \(B\) và \(C\). Vẽ đường kính \(AOD\). Xác định vị trí điểm \(A\) để diện tích \(\bigtriangleup ABC\) đạt giá trị lớn nhất, khi đó \(\widehat{ADC}=?\)

Hướng dẫn: Vẽ đường cao \(AH\) của \(\bigtriangleup ABC\).
\(\bigtriangleup AHO\) vuông tại \(H\) nên \(AH\leq AO\) (dấu bằng xảy ra khi \(H\equiv O\))
\(S_{ABC}=\frac{1}{2}AH.BC\leq \frac{1}{2}.AO.BC=\frac{1}{2}R.2R=R^2\)(dấu bằng xảy ra khi \(H\equiv O\))
Vậy diện tính tam giác \(ABC\) đạt giá trị lớn nhất khi \(H\equiv O\), khi đó \(A\) là điểm chính giữa \(\stackrel\frown{BC}\)
Suy ra \(\widehat{ADC}=45^0\)
Bài 2: Cho nửa đường tròn đường kính \(AB=2cm\), dây \(CD//AB (C\in\stackrel\frown{AD})\). Tính độ dài các cạnh của hình thang \(ABCD\) biết chu vi hình thang bằng \(5cm\)
.png)
Hướng dẫn: Ta có \(CD//AB\Rightarrow \stackrel\frown{AC}=\stackrel\frown{BD}\Rightarrow AC=BD\). Dễ chứng minh \(ABDC\) là hình thang cân (vì \(\widehat{CAB}=\widehat{DBA}\))
Đặt \(AC=BD=x\) \((x>0)\), chu vi hình thang bằng \(5cm\) nên \(AB+BD+CD+AC=5\Rightarrow CD=3-2x\)
Kẻ \(DN,CM\) vuông góc với \(AB\). Ta có \(NB=MA=\frac{AB-CD}{2}=\frac{2-(3-2x)}{2}=\frac{2x-1}{2}\)
\(\bigtriangleup DAB\) vuông tại \(D\) có \(DN\perp AB\) nên \(BD^2=BN.BA\Rightarrow x^2=\frac{2x-1}{2}.2\Rightarrow x^2-2x-1=0\Rightarrow x=1\)
Vậy \(AC=BD=1cm\) , do đó \(CD=3-2x=1 (cm)\)
3. Luyện tập Bài 3 Chương 3 Hình học 9
Qua bài giảng Góc nội tiếp này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Nắm vững định nghĩa, định lí, hệ quả góc nội tiếp
- Vận dụng lý thuyết làm được một số bài tập
3.1 Trắc nghiệm về Góc nội tiếp
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Bài 3 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- B. Góc nội tiếp chắn nửa đường tròn là góc vuông.
- C. Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
- D. Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
-
- A. 500
- B. 600
- C. 700
- D. 800
Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online
3.2 Bài tập SGK về Góc nội tiếp
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 9 Bài 3 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9 tập 1
Bài tập 16 trang 75 SGK Toán 9 Tập 2
Bài tập 17 trang 75 SGK Toán 9 Tập 2
Bài tập 18 trang 75 SGK Toán 9 Tập 2
Bài tập 19 trang 75 SGK Toán 9 Tập 2
Bài tập 20 trang 76 SGK Toán 9 Tập 2
Bài tập 21 trang 76 SGK Toán 9 Tập 2
Bài tập 22 trang 76 SGK Toán 9 Tập 2
Bài tập 23 trang 76 SGK Toán 9 Tập 2
Bài tập 24 trang 76 SGK Toán 9 Tập 2
Bài tập 25 trang 76 SGK Toán 9 Tập 2
Bài tập 26 trang 76 SGK Toán 9 Tập 2
Bài tập 3.1 rang 103 SBT Toán 9 Tập 2
4. Hỏi đáp Bài 3 Chương 3 Hình học 9
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 9
Lớp 9 - Là năm cuối ở cấp trung học cơ sở, sắp phải bước vào một kì thi căng thẳng và sắp chia tay bạn bè, thầy cô và cả kì vọng của phụ huynh ngày càng lớn mang tên "Lên cấp 3". Thật là áp lực nhưng các em hãy cứ tự tin vào bản thân là sẻ vượt qua nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK