Lý thuyết đoạn mạch song song chuẩn nhất

Đoạn mạch song song là một trong những kiến thức quan trọng thuộc chương I nghiên cứu về Điện học của môn Vật lý 9. xin gửi tới các bạn lý thuyết đoạn mạch song song và các dạng bài tập vật lý đoạn mạch song song đầy đủ và chi tiết nhất. Mong với các tài liệu về bài 5 đoạn mạch song song sẽ giúp ích các bạn!

A. Tóm tắt một số kiến thức cần nhớ về đoạn mạch song song 

1. Yếu tố về độ lớn của cường độ dòng điện và hiệu điện thế 

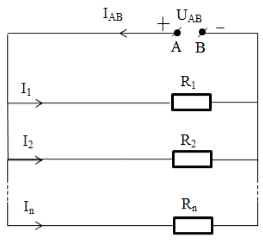
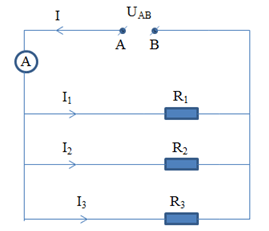
Một đoạn mạch được mắc theo dạng song song với một số lượng điện trở nhất định theo như hình vẽ phía dưới:

Với hình vẽ trên ta có các chú thích sau:

- \(R_{1}\), \(R_{2}\), \(R_{3}\) được kí hiệu là các điện trở được đặt trong mạch song song

- Trong vị trí hai đầu đoạn mạch có hiệu điện thế được kí hiệu là \(U_{AB}\)

- Khi chạy qua các điện trở có trong đoạn mạch đều có các cường độ dòng điện, cường độ dòng điện này có độ lớn được kí hiệu là \(I_{1}\), \(I_{2}\), \(I_{3}\)

- Độ lớn của cường độ dòng điện đi qua mạch chính được kí hiệu là \(I_{AB}\)

Từ những yếu tố có trong đoạn mạch song song, ta có một số công thức về mối liên hệ giữa các yếu tố như sau:

- Tổng cường độ dòng điện chạy qua các điện trở chính bằng cường độ của dòng điện chạy qua mạch chính.

\(I_{AB}\) = \(I_{1}\) + \(I_{2}\) + \(I_{3}\)

Hiệu điện thế ở vị trí hai đầu đoạn mạch sẽ có độ lớn bằng hiệu điện thế của các điện trở được đặt ở trong vị trí mỗi đoạn mạch rẽ song song.

\(U=U_{1}=U_{2} = U_{3}\)

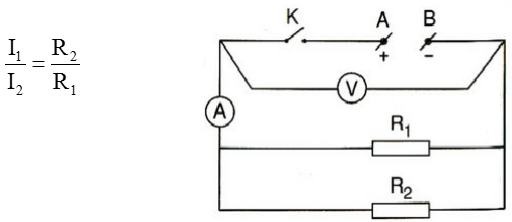
- Mối tương quan giữa cường độ dòng điện và hiệu điện thế giữa hai đầu đoạn mạch của một điện trở có dạng mắc song song. Điện trở sẽ tỉ lệ nghịch với cường độ dòng điện chạy qua điện trở đó.

2. Đặc điểm của điện trở tương đương trong một đoạn mạch có dạng mắc là song song 

Trong một đoạn mạch có dạng mắc là song song, ta có tính chất là tổng nghịch đỏa của từng điện trở thành phần sẽ đúng bằng điện trở tương đương:

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}\) => \(R_{tđ}=\dfrac{R_{1}.R_{2}}{R_{1}+R_{2}}\)

Công thức suy rộng ta có:

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+...+\dfrac{1}{R_{n}}\)

3. Liên hệ đoạn mạch song song với thực tế

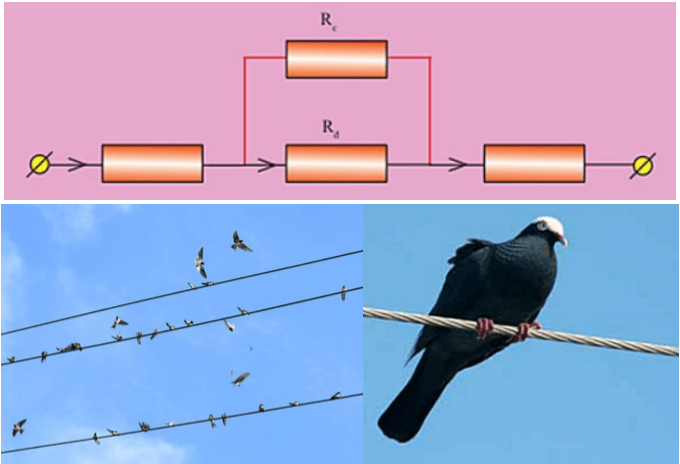
Trong cuộc sống, ở những dây dẫn điện thuộc trung thế và cao thế được mắc ở các cột điện chạy ở môi trường bình thường thường ở trong điều kiện là không có vỏ bọc để cách điện. Nhưng có một hiện tượng là khi những con chim bay lên và đậu ở trên các dây điện trung và cao thế này mà không bị điện giật.

=> Ta có thể lý giải lý do đó như sau:

Khi những con chim đậu lên bên trên những dây điện trung và cao thế thì cơ thể chim có vai trò là một điện trở mắc ở dạng song song so với đoạn dây dẫn giữa hai chân của con chim. Với điện trở \(R_{c}\) của khối lượng cơ thể con chím là rất lớn so với điện trở của đoạn dây dẫn ở vị trí giữa hay chân chim nên cường độ của dòng điện qua cơ thể chim là rất nhỏ nên không bị ảnh hưởng đến chim

B. Một số bài tập về đoạn mạch song song

1. Một số bài tập trắc nghiệm đoạn mạch song song

Câu 1: Cho một đoạn mạch được mắc theo dạng song song với hai điện trở được kí hiệu là \(R_{1}\) và \(R_{2}\) và các hiệu điện thế toàn mạch và các hiệu điện thế đi qua hai điện trở \(R_{1}\) và \(R_{2}\) được kí hiệu lần lượt là \(U\), \(U_{1}\), \(U_{2}\). Chọn một biểu thức đúng trong các biểu thức thức sau đây:

\(A.U=U_{1}=U_{2}\)

\(B.U=U_{1}+U_{2}\)

\(C.U\neq U_{1}+U_{2}\)

\(D.U_{1}\neq U_{2}\)

Câu 2: Chọn biểu thức đúng trong các biểu thức sau đây khi nói về điện trở tương đương trong một đoạn mạch có dạng mắc là song song?

\(A.R_{tđ}=R_{1}+R_{2}\)

\(B.R_{tđ}=\dfrac{R_{1}.R_{2}}{R_{1}-R_{2}}\)

\(C.\dfrac{1}{R_{tđ}}= \dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}\)

\(D.R_{tđ}=R_{1}-R_{2}\)

Câu 3: Một đoạn mạch được mắc có dạng song song với hai điện trở thứ nhất là \(R_{1}\) có độ lớn bằng 6\(\Omega \) và điện trở thứ hai là \(R_{2}\). Biết rằng \(I=1,2A\) và \(I_{2}=0,4A\) lần lượt là cường độ dòng điện của mạch chính và cường độ dòng điện đi qua điện trở thứ hai. Vậy độ lớn của điện trở \(R_{2}\) là:

\(A. 10\Omega \)

\(B. 12\Omega \)

\(C. 15\Omega\)

\(D. 13\Omega \)

Câu 4: Một đoạn mạch có dạng mắc là song song với hai điện trở được kí hiệu là \(R_{1}\) và \(R_{2}\) có độ lớn lần lượt là \(6\Omega \) và \(3\Omega \) kết nối với hai vị trí với hiệu điện thế là \(6V\). Qua mạch chính, cường độ dòng điện và điện trở tương đương có độ lớn là:

\(A. I=0,6A, R=9\Omega\)

\(B. I=1A, R=9\Omega\)

\(C. I=1A, R=2\Omega \)

\(D. I=3A, R=2\Omega \)

Câu 5: Một đoạn mạch có dạng mắc song song với hai điện trở được kí hiệu là \(R_{1}\) và \(R_{2}\) có độ lớn lần lượt là \(15\Omega \) và \(10\Omega \) với các cường độ dòng điện tối đa với hai điện trở lần lượt là 2A và 1A. Giá trị lớn nhất mà hiệu điện thế có thể đặt vào vị trí hai đầu đoạn mạch chứa hai điện trở \(R_{1}\) và \(R_{2}\) là:

\(A. 40V\)

\(B. 10V\)

\(C. 30V\)

\(D. 25V\)

2. Một số bài tập tự luận về bài 5 đoạn mạch song song

Bài 1: Một đoạn mạch có dạng mắc song song với hai điện trở được kí hiệu lần lượt là \(R_{1}\), \(R_{2}\) và \(R_{3}\) với độ lớn lần lượt là \(20\Omega \), \(30\Omega \) và \(60\Omega \). Biết rằng độ lớn của cường độ dòng điện qua điện trở \(R_{2}\) là 0,6A, hỏi qua mạch chính và qua hai điện trở còn lại là bao nhiêu?

Hướng dẫn giải bài tập bài 1:

Ta có công thức tính điện trở tương đương có trong một đoạn mạch được mắc dạng song song là:

\(\dfrac{1}{R_{123}}\) = \(\dfrac{1}{R_{1}}\) + \(\dfrac{1}{R_{2}}\) + \(\dfrac{1}{R_{3}}\) => \(\dfrac{1}{R_{123}}\) = \(\dfrac{1}{20}\) + \(\dfrac{1}{30}\) + \(\dfrac{1}{60}\) = \(\dfrac{18}{180}\) => \(R_{123}=10\Omega \)

Từ đó, suy ra được hiệu điện thế trong mỗi điện trở và giữa hai đầu đoạn mạch là:

\(U=U_{1}=U_{2}=U_{3}\) = \(I_{2}.R_{2}\) = \(0,6.30\) = \(18V\)

Vậy qua mạch chính của đoạn mạch được mắc song song thì cường độ của dòng điện có độ lớn là:

\(I=\dfrac{U}{R_{123}}\) = \(\dfrac{18}{10}\) = 1,8V

Vì đoạn mạch được mắc theo dạng là song song nên ta có:

\(I=I_{1}+I_{2}+I_{3}\) => \(I_{1}+I_{3}\) = \(I-I_{2}\) = 1,8 - 0,6 = 1,2A

Mặt khác, ta lại có: \(\dfrac{I_{1}}{I_{3}}=\dfrac{R_{1}}{R_{3}}\) = \(\dfrac{60}{20}\) = 3 => \(I_{1}=I_{3}.\dfrac{R_{3}}{R_{1}}\) = \(3I_{3}\)

Vậy \(I_{3}=0,3A\) và \(I_{1}=0,9A\)

Bài 2: Một mạch điện được mắc dạng song song như hình vẽ. Cho công thức liên hệ về độ lớn giữa các điện trở là \(R_{1}\) = 2\(R_{2}\) = 3\(R_{3}\)và giá trị của hiệu điện thế ở vị trí giữa hai đầu AB là 48V. Biết rằng đoạn mạch dạng song song được mắc vào bằng một ampe kế chỉ là 1,6A, hãy tính độ lớn của các điện trở được mắc trong đoạn mạch dạng song song?

Hướng dẫn làm bài tập bài 2:

Theo công thức về đoạn mạch song song ta có:

\(R=\dfrac{U}{I}\) = \(\dfrac{48}{1,6}\) = \(30\Omega \)

Mà mặt khác ta có:

\(\dfrac{1}{R_{123}}\) = \(\dfrac{1}{R_{1}}\) + \(\dfrac{1}{R_{2}}\) + \(\dfrac{1}{R_{3}}\) => \(\dfrac{1}{R_{123}}\) = \(\dfrac{1}{3.R_{3}}\) + \(\dfrac{1}{1,5.R_{3}}\) + \(\dfrac{1}{R_{3}}\) => \(\dfrac{1}{R_{123}}\) = \(\dfrac{1+2+3}{3.R_{3}}\) 

=> \(\dfrac{1}{R_{123}}\) = \(\dfrac{2}{R_{3}}\) => R = \(\dfrac{R_{3}}{2}\)

Vậy \(R_{1}\) = 180\(\Omega \), \(R_{2}\) = 90\(\Omega \), \(R_{3}\) = 60\(\Omega \)

Bài 3: Cho 100\(\Omega \) là độ lớn của điện trở của một đoạn dây dẫn. Ở vị trí hai đâu dây dẫn, mắc vào đó một hiệu điện thế có giá trị là một hằng số \(U=36V\). Hỏi

a, Qua đoạn dây dẫn đó, cường độ của dòng điện là bao nhiêu?

b, Có hai cách để thay đổi cường độ của dòng điện trong đoạn dây lên mức 1,5A, đó là:

- Bỏ bớt một phần về độ dài của đoạn dây và trên đoạn phần cắt bỏ đó, ta tính điện trở.

- Đoạn dây được chia thành hai phần. Trên mỗi phần của đoạn dây, mắc vào đó một điện trở lần lượt là \(R_{1}\) và \(R_{2}\) với một điều kiện là \(R_{1}\) > \(R_{2}\). Sau đó, ghép hai phần của dây theo dạng mắc song song rồi tính độ lớn của mỗi điện trở.

Hướng dẫn giải bài tập bài 3:

a, Qua đoạn dây dẫn đó, cường độ của dòng điện là \(I=\dfrac{U}{R}\) = \(\dfrac{36}{100}\) = \(0,36A\)

b, Muốn cường độ của dòng điện chạy trong đoạn dây dẫn là 1,5A thì khi đó 

\(R'=\dfrac{U}{I}\) = \(\dfrac{36}{1,5}\) = \(24\Omega \)

Với các làm thứ nhất, phần cắt bỏ có điện trở là:

\(R_{cb}=R-R'\) = \(100-24\) = \(76\Omega \)

Với cách làm thứ hai, thì điện trở tương đương của toàn mạch là:

\(R_{tđ}'=\dfrac{R_{1}.R_{2}}{R_{1}+R_{2}}\) và \(R'=24\Omega\) => \(24=\dfrac{R_{1}.R_{2}}{R_{1}+R_{2}}\)

Mà theo dữ kiện đề bài ta có \(R_{1}+R_{2}=100\) => \(R_{1}.R_{2}=100.24\) = \(2400\)

Từ đó, ta có thể lập được hệ phương trình:

\(\left\{\begin{matrix}R_{1}+R_{2}=100\\ R_{1}.R_{2}=2400\end{matrix}\right. \) => \(\left\{\begin{matrix}R_{1}=60\Omega \\ R_{2}=40\Omega \end{matrix}\right. \)

Bài 4: Biết rằng một đoạn mạch được mắc như hình vẽ. Biết rằng đoạn mạch được mắc với một vôn kế chỉ 36V và một ampe kế chỉ 3A và độ lớn của điện trở thứ nhất \(R_{1}\) = 30\(\Omega \). Hỏi:

a, Độ lớn của điện trở \(R_{2}\) là bao nhiêu?

b, Các ampe kế \(A_{1}\) và \(A_{2}\) có số chỉ là bao nhiêu?

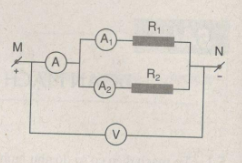
Hướng dẫn giải bài tập bài 4:

a, Ta có: 

\(\dfrac{R_{1}.R_{2}}{R_{1}+R_{2}}=\dfrac{U}{I}\) = \(\dfrac{36}{3}=12\) => \(R_{2}\) = 20\(\Omega \)

b, Ampe kế \(A_{1}\) có số chỉ là \(I_{1}=\dfrac{U}{R_{1}}\) = \(\dfrac{36}{30}=1,2A\)

Ampe kế \(A_{2}\) có số chỉ là: \(I_{2}=I-I_{1}=3-1,2=1,8A\)

Tham khảo thêm >>> Giải bài tập vật lý Đoạn mạch song song

đã đem đến cho các bạn phần lý thuyết lý thuyết đoạn mạch song song và các dạng bài tập về điện trở tương đương của đoạn mạch song song thông qua bài viết bài 5 đoạn mạch song song. Nếu có đóng góp hay thắc mắc gì cho bài viết Bài 5 đoạn mạch song song, các bạn hãy để lại comment dưới phần bình luận nhé!