Tổng hợp lý thuyết chuẩn nhất về đường thẳng vuông góc với mặt phẳng

Trong bài viết tổng hợp các bài tập đường thẳng vuông góc với mặt phẳng, đồng thời đưa ra những kiến thức lý thuyết nền căn bản trong chuyên đề đường thẳng vuông góc với mặt phẳng như các chứng minh đường thẳng vuông góc với mặt phẳng và viết phương trình mặt phẳng đi qua 1 điểm và vuông góc với đường thẳng.

I) Tìm hiểu chung

1) Khái niệm

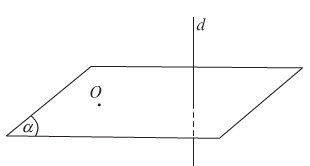
Đường thẳng được gọi là vuông góc với mặt phẳng khi nó vuông góc với mọi đường thẳng thuộc mặt phẳng.

2) Điều kiện

Để đường thẳng vuông góc với mặt phẳng thì ta có điều kiện sau: đường thẳng phải vuông góc với 2 đường thẳng giao nhau nằm trong mặt phẳng.

II) Phương pháp chứng minh đường thẳng vuông góc với mặt phẳng

Cho đường thẳng d và mặt phẳng (P), chứng minh đường thẳng d vuông góc với mặt phẳng (P)

1) Phương pháp 1

Để chứng minh \(d \perp (P)\) ta cần chứng minh được d vuông góc với 2 đường thẳng a và b, a và b cắt nhau nằm trong mặt phẳng (P)

2) Phương pháp 2

Ta sử dụng tính chất hai đường thẳng song song với nhau, đường thẳng này vuông góc với mặt phẳng thì đường thẳng kia cũng vuông góc với mặt phẳng đó.

VD: Đường thẳng d song với đường thẳng \(\Delta\), mà \(\Delta \perp (P)\). Suy ra \(d\perp (P)\)

3) Phương pháp 3

Ta sử dụng định lý:

Cho (P) và (Q) vuông góc và cắt nhau theo giao tuyến x. Một đường thẳng bất kì nằm trong mặt phẳng (P) mà vuông góc với giao tuyến x thì đường thẳng đó vuông góc với mặt phẳng (Q).

4) Phương pháp 4

Ở phương pháp này ta sử dụng tính chất hai mặt phẳng phân biệt đều cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của hai mặt phẳng đó cũng vuông góc với mặt phẳng thứ 3.

5) Phương pháp 5

Phương pháp 5 ta sử dụng tính chất hai mặt phẳng song song với nhau, mặt phẳng này vuông góc với đường thẳng thì mặt phẳng kia cũng vuông góc với đường thẳng đó.

6) Phương pháp 6

Trái với phương pháp 5, ở phương pháp này tuy ta cũng sử dụng tính chất nhưng là tính chất hai đường thẳng song song, đường thẳng này vuông góc với một mặt phẳng thì đường thẳng kia cũng vuông góc với mặt phẳng đó.

III) Các viết phương trình mặt phẳng đi qua 1 điểm và vuông góc với đường thẳng

Cho đường thẳng d và mặt phẳng (P), viết phương trình mặt phẳng (P) đi qua 1 điểm và vuông góc với đường thẳng d.

Bước 1: Ta tìm vecto chỉ phương (VTCP) của d là \(\underset{u_d}{\rightarrow}\)

Bước 2: Vì \(d \perp (P)\) nên (P) có VTPT là \(\underset{n_{(P)}}{\rightarrow} = \underset{n_d}{\rightarrow}\)

Bước 3: Áp dụng cách viết phương trình đi qua 1 điểm có VTPT \(\underset{n_{(P)}}{\rightarrow}\)

IV) Luyện tập

Tại phần này chúng ta sẽ đi vào tìm hiểu và giải quyết các bài tập đường thẳng vuông góc với mặt phẳng.

Bài tập 1: Trong hệ tọa độ không gian Oxyz viết phương trình mặt phẳng qua M và vuông với NP. Biết rằng M(2;-1;1), N(1;0;4), P(0; -2; -1).

Đáp án

Phương trình mặt phẳng qua M và vuông góc với NP là: x + 2y + 5z - 5 = 0

Bài tập 2: Cho điểm A(2; 5; 1) nằm trong không gian hệ tọa độ Oxyz. Hãy viết phương trình mặt phẳng qua A và vuông góc với Oy.

Đáp án

Phương trình mặt phẳng qua A và vuông góc với Oy là: y - 5 = 0

Bài tập 3: Điểm A(-2; 3; 1) nằm trong không gian hệ tọa độ Oxyz. Viết phương trình mặt phẳng đi qua A và vuông với d, biết phương trình d có dạng:\(\dfrac{x+1}{-2}= \dfrac{y-3}{1}=\dfrac{z+4}{3}\)

Đáp án

Phương trình mặt phẳng đi qua A và vuông góc với d là: -2x + y + 3z - 10 = 0

Trên đây là bài viết mà đã tổng hợp được về cách chứng minh đường thẳng vuông góc với mặt phẳng và bài tập đường thẳng vuông góc với mặt phẳng. Hy vọng bài viết về chuyên đề đường thẳng vuông góc với mặt phẳng sẽ giúp ích được nhiều cho bạn.