Lý thuyết Tổng và hiệu của hai vectơ

Ở bài viết này sẽ gửi đến cho các bạn học lý thuyết về tổng và hiệu của hai vectơ chuẩn nhất, hy vọng cùng với các bài tập về tổng và hiệu của hai vectơ toán 10 sẽ giúp ích được cho quá trình học tập của các bạn.

A. Lý thuyết

I. Tổng

1. Quy tắc cộng 1: Cộng ba điểm (nối đuôi)

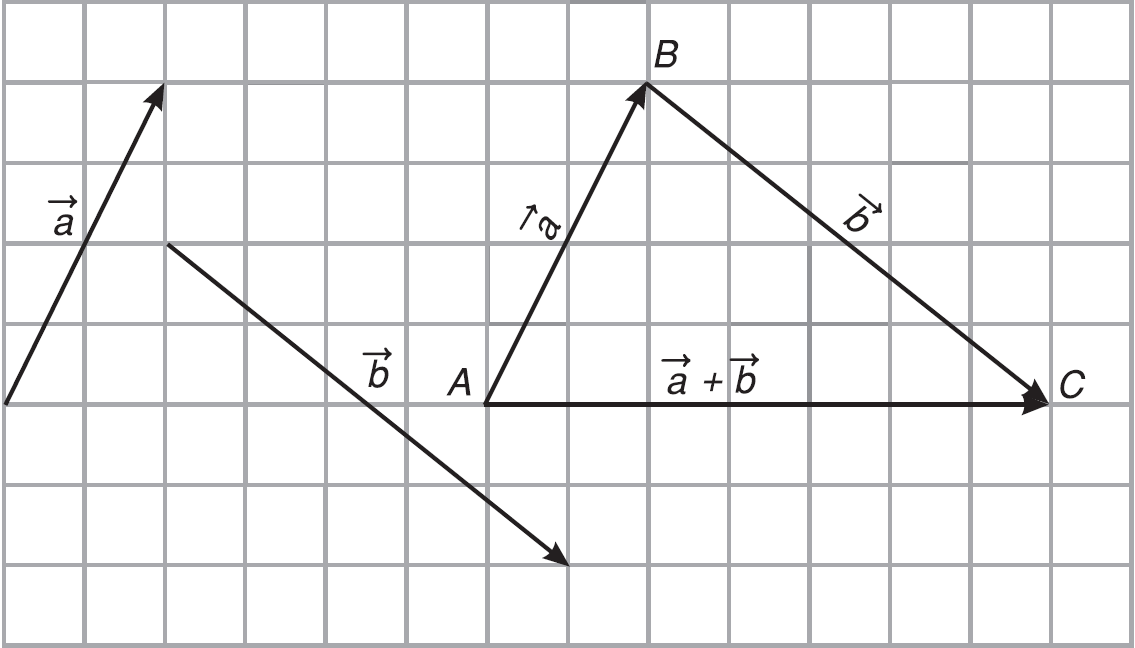
- Định nghĩa: Cho trước hai vectơ \(\underset{a}{\rightarrow}, \underset{b}{\rightarrow}\). Lấy một điểm A bất kỳ, vẽ vectơ \(\underset{AB}{\rightarrow} = \underset{a}{\rightarrow}\), \(\underset{BC}{\rightarrow}=\underset{b}{\rightarrow}\). Lúc này vectơ \(\underset{AC}{\rightarrow}\) sẽ được gọi là tổng của hai vectơ \(\underset{a}{\rightarrow}\) và \(\underset{b}{\rightarrow}\)

- Ký hiệu: \(\underset{AC}{\rightarrow}=\underset{a}{\rightarrow}+\underset{b}{\rightarrow}\), \(\forall A, B, C\)

2. Quy tắc hình bình hành (chung đầu tổng)

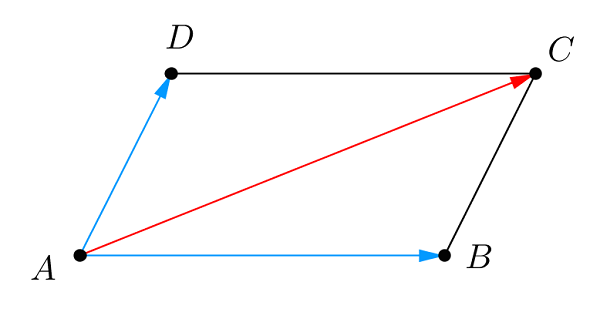
Cho tứ giác ABCD. Nếu tứ giác ABCD là hình bình hành thì ta được: \(\underset{AC}{\rightarrow}=\underset{AB}{\rightarrow}+\underset{AD}{\rightarrow}\)

3. Chú ý: 

- Nếu ba điểm A, B, C  thẳng hàng thì cộng theo quy tắc kéo co

 \(\underset{OA}{\rightarrow}+\underset{OB}{\rightarrow}=\underset{0}{\rightarrow}\)

\(\underset{OA}{\rightarrow}+\underset{OC}{\rightarrow}=\underset{BC}{\rightarrow}\)

- Tính chất của tổng các vectơ

• Tính chất giao hoán: \(\underset{a}{\rightarrow}+\underset{b}{\rightarrow}=\underset{b}{\rightarrow}+\underset{a}{\rightarrow}\)
• Tính chất kết hợp: \((\underset{a}{\rightarrow}+\underset{b}{\rightarrow})+\underset{c}{\rightarrow}=\underset{a}{\rightarrow}+(\underset{b}{\rightarrow}+\underset{c}{\rightarrow})\)
• Tính chất của \(\underset{0}{\rightarrow}\):  \(\underset{a}{\rightarrow}+\underset{0}{\rightarrow}=\underset{0}{\rightarrow}+\underset{a}{\rightarrow}\)

II. Hiệu

1. Vectơ đối

- Khái niệm: Là vectơ mà có cùng độ dài nhưng ngược hướng với vectơ \(\underset{a}{\rightarrow}\) thì sẽ được gọi là vectơ đối của vectơ \(\underset{a}{\rightarrow}\).

- Ký hiệu: -\(\underset{a}{\rightarrow}\)

- Vectơ đối của \(\underset{0}{\rightarrow}=​​\underset{0}{\rightarrow}\)

2. Hiệu của hai vectơ

- Khái niệm: Cho hai vectơ \(\underset{a}{\rightarrow}, \underset{b}{\rightarrow}\). Vectơ hiệu của hai vectơ, kí hiệu \(​​​​\underset{a}{\rightarrow}-\underset{b}{\rightarrow}\) là vectơ \(​​​​\underset{a}{\rightarrow}+ (-\underset{b}{\rightarrow})\)

- Ký hiệu: \(\underset{a}{\rightarrow}-\underset{b}{\rightarrow}=​​​​​​​​\underset{a}{\rightarrow}+ (-\underset{b}{\rightarrow})\)

3. Quy tắc ba điểm (quy tắc tam giác)

A, B, C là ba điểm được cho bất kỳ, khi đó ta được:   \(\underset{AB}{\rightarrow}-\underset{AC}{\rightarrow}=​​​​\underset{CB}{\rightarrow}\)

III. Các hệ thức vectơ

1. Trung điểm của đoạn thẳng

Cho đoạn thẳng AB, I là trung điểm của đoạn thẳng, ta được: \(\underset{IA}{\rightarrow}+\underset{IB}{\rightarrow}=​​​​\underset{0}{\rightarrow}\)

2. Trọng tâm của tam giác

Ba điểm A, B, C hợp thành một tam giác, lấy G là trọng tâm của tam giác ABC, ta được: \(\underset{GA}{\rightarrow}+\underset{GB}{\rightarrow}+ \underset{GC}{\rightarrow}=​​​​\underset{0}{\rightarrow}\)

B. Bài tập về tổng và hiệu của hai vectơ

Câu 1: Hai vectơ \(\underset{a}{\rightarrow}\) và \(\underset{b}{\rightarrow}\) là hai vectơ khác \(\underset{0}{\rightarrow}\), \(\underset{a}{\rightarrow}\) là vectơ đối của  \(\underset{b}{\rightarrow}\). Yêu cầu hãy chọn khẳng định đúng nhất trong các khẳng định dưới.

A. Hai vectơ  \(\underset{a}{\rightarrow}\) và \(\underset{b}{\rightarrow}\) cùng phương

B. Hai vectơ  \(\underset{a}{\rightarrow}\) và \(\underset{b}{\rightarrow}\) chung điểm đầu

C. Hai vectơ  \(\underset{a}{\rightarrow}\) và \(\underset{b}{\rightarrow}\)  ngược hướng

D. Hai vectơ  \(\underset{a}{\rightarrow}\) và \(\underset{b}{\rightarrow}\) cùng độ dài

=> Đáp án đúng: B.

=> Suy ra hai vectơ  \(\underset{a}{\rightarrow}\) và \(\underset{b}{\rightarrow}\) cùng phương, cùng độ dài và ngược hướng với nhau

Câu 2: A, B, C là ba điểm phân biệt. Trong bốn đẳng thức sau, đâu là đẳng thức đúng nhất?

A.  \(\underset{CA}{\rightarrow}-\underset{BA}{\rightarrow}=​​​​\underset{BC}{\rightarrow}\)

B.  \(\underset{AB}{\rightarrow}+\underset{AC}{\rightarrow}=​​​​\underset{BC}{\rightarrow}\)

C.  \(\underset{AB}{\rightarrow}+\underset{CA}{\rightarrow}=​​​​\underset{CB}{\rightarrow}\)

D.  \(\underset{AB}{\rightarrow}-\underset{BC}{\rightarrow}=​​​​\underset{CA}{\rightarrow}\)

=> Đáp án đúng: C

=> Lý giải: \(\underset{AB}{\rightarrow}+\underset{CA}{\rightarrow}=\underset{CA}{\rightarrow}+\underset{AB}{\rightarrow}=\underset{CB}{\rightarrow}\)

Câu 3: Cho \(\underset{AB}{\rightarrow}=-\underset{CD}{\rightarrow}\). Đâu là khẳng định đúng?

A. \(\underset{AB}{\rightarrow} \) và \(\underset{CD}{\rightarrow}\) cùng hướng

B.  \(\underset{AB}{\rightarrow} \) và \(\underset{CD}{\rightarrow}\)  cùng độ dài

C. Tứ giác ABCD là hình bình hành

D. \(\underset{AB}{\rightarrow} \) +  \(\underset{DC}{\rightarrow} =​​\underset{0}{\rightarrow}\)

=> Đáp án đúng: B

=> Lý giải: 

- Ta có: \(\underset{AB}{\rightarrow}=-\underset{CD}{\rightarrow} = \underset{CD}{\rightarrow}\)

- Do đó:

• \(\underset{AB}{\rightarrow}\) và  \(\underset{CD}{\rightarrow}\) ngược hướng
• \(\underset{AB}{\rightarrow}\) và  \(\underset{CD}{\rightarrow}\)  có cùng độ dài
• Nếu \(\underset{AB}{\rightarrow}\) và  \(\underset{CD}{\rightarrow}\) không cùng giá thì tứ giác ABCD sẽ là hình bình hành
• \(\underset{AB}{\rightarrow}\) + \(\underset{CD}{\rightarrow}\) = \(\underset{0}{\rightarrow}\)

Câu 4: Tính tổng \(\underset{MN}{\rightarrow}+\underset{PQ}{\rightarrow}+\underset{RN}{\rightarrow}+\underset{NP}{\rightarrow}+ \underset{QR}{\rightarrow}\)

A. \(\underset{MR}{\rightarrow}\)

B. \(\underset{MN}{\rightarrow}\)

C. \(\underset{PR}{\rightarrow}\)

D. \(\underset{MP}{\rightarrow}\)

=> Đáp án đúng: B

=> Lý giải: \(\underset{MN}{\rightarrow}+\underset{PQ}{\rightarrow}+\underset{RN}{\rightarrow}+\underset{NP}{\rightarrow}+ \underset{QR}{\rightarrow}\) = \(\underset{MN}{\rightarrow}+\underset{NP}{\rightarrow}+\underset{PQ}{\rightarrow}+\underset{QR}{\rightarrow}+ \underset{RN}{\rightarrow} = \underset{MN}{\rightarrow}\)

Câu 5: Cho điểm A và B phân biệt. Để đoạn AB có thể có điểm I là trung điểm thì?

A. IA=IB

B. \(\underset{IA}{\rightarrow}=\underset{IB}{\rightarrow}\)

C. \(\underset{IA}{\rightarrow}=-\underset{IB}{\rightarrow}\)

D. \(\underset{AI}{\rightarrow}=-\underset{BI}{\rightarrow}\)

=> Đáp án đúng: B

Câu 6: Hãy chọn đáp án thể hiện được điều kiện cần và đủ để I trở thành trung điểm của đoạn thẳng AB?

A. IA=IB

B.  \(\underset{IA}{\rightarrow}+\underset{IB}{\rightarrow}=​​\underset{0}{\rightarrow}\)

C. \(\underset{IA}{\rightarrow}-\underset{IB}{\rightarrow}=​​\underset{0}{\rightarrow}\)

D. \(\underset{IA}{\rightarrow}=\underset{IB}{\rightarrow}\)

=> Đáp án đúng: B

=> Lý giải: \(\underset{IA}{\rightarrow}=-\underset{IB}{\rightarrow} \Leftrightarrow \underset{IA}{\rightarrow}+\underset{IB}{\rightarrow}=\underset{0}{\rightarrow}\)

Câu 7: Cho tam giác​​ ABC​​ cân ở​​ A, đường cao​​ AH. Đâu là khẳng định sai?

A. \(\underset{AB}{\rightarrow}=\underset{AC}{\rightarrow}\)

B. \(\underset{HC}{\rightarrow}=-\underset{HB}{\rightarrow}\)

C. \(\left | \underset{AB}{\rightarrow} \right |=\left | \underset{AC}{\rightarrow} \right |\)

D. \(\underset{BC}{\rightarrow}\)= 2\(\underset{HC}{\rightarrow}\)

=> Đáp án đúng: A

Câu 8: Cho hình vuông​​ ABCD. Khẳng định đúng nhất là?

A. \(\underset{AB}{\rightarrow}=\underset{BC}{\rightarrow}\)

B. \(\underset{AB}{\rightarrow}=\underset{CD}{\rightarrow}\)

C. \(\underset{AC}{\rightarrow}=\underset{BD}{\rightarrow}\)

D. \(\left | \underset{AD}{\rightarrow} \right |=\left | \underset{CB}{\rightarrow} \right |\)

=> Đáp án đúng: D

Câu 9: Gọi​​ O là tâm hình bình hành​​ ABCD. Hãy chọn ra đẳng thức sai?

A. \(\underset{OA}{\rightarrow}-\underset{OB}{\rightarrow}=\underset{CD}{\rightarrow}\)

B. \(\underset{OB}{\rightarrow}-\underset{OC}{\rightarrow}=\underset{OD}{\rightarrow}-\underset{OA}{\rightarrow}\)

C. \(\underset{AB}{\rightarrow}-\underset{AD}{\rightarrow}=\underset{DB}{\rightarrow}\)

D. \(\underset{BC}{\rightarrow}-\underset{BA}{\rightarrow}=\underset{DC}{\rightarrow}-\underset{DA}{\rightarrow}\)

=> Đáp án đúng: B

Câu 10: Gọi​​ M,  N,  P lần lượt là trung điểm các cạnh​​ AB,  BC,  CA của tam giác​​ ABC. Hỏi vectơ \(\underset{MN}{\rightarrow}+\underset{NP}{\rightarrow}\) bằng vectơ nào trong các vectơ sau đây?

A. \(\underset{AP}{\rightarrow}\)

B. \(\underset{BP}{\rightarrow}\)

C. \(\underset{MN}{\rightarrow}\)

D. \(\underset{MB}{\rightarrow}+\underset{NB}{\rightarrow}\)

=> Đáp án đúng: B

Câu 11: Cho tam giác vuông ABC, biết trước G là trọng tâm của tam giác, độ dài cạnh huyền BC là 12. Hỏi rằng độ dài của vectơ​​ \(\underset{v}{\rightarrow}=\underset{GB}{\rightarrow}+\underset{GC}{\rightarrow}\) là bao nhiêu?

A. \(\left | \underset{v}{\rightarrow} \right |\) = 2

B. \(\left | \underset{v}{\rightarrow} \right |\) = \(2\sqrt{3}\)

C. \(\left | \underset{v}{\rightarrow} \right |\) = 8

D. \(\left | \underset{v}{\rightarrow} \right |\) = 4

=> Đáp án đúng: D

Câu 12: Cho hình thoi​​ ABCD​​ có​​ AC=2a và​​ BD=a. Tính​​ \(\left | \underset{AC}{\rightarrow}+ \underset{BD}{\rightarrow}\right |\).

A. \(\left | \underset{AC}{\rightarrow}+ \underset{BD}{\rightarrow}\right |\) = 3a

B. \(\left | \underset{AC}{\rightarrow}+ \underset{BD}{\rightarrow}\right |\) = a\(\sqrt{3}\)

C. \(\left | \underset{AC}{\rightarrow}+ \underset{BD}{\rightarrow}\right |\) = a\(\sqrt{5}\)

D. \(\left | \underset{AC}{\rightarrow}+ \underset{BD}{\rightarrow}\right |\) = 5a

=> Đáp án đúng: C

Câu 13: Cho hình vuông​​ ABCD cạnh​​ a. Tính \(\left | \underset{AB}{\rightarrow}- \underset{DA}{\rightarrow}\right |\)

A. \(\left | \underset{AB}{\rightarrow}- \underset{DA}{\rightarrow}\right |\) = 0

B. \(\left | \underset{AB}{\rightarrow}- \underset{DA}{\rightarrow}\right |\) = a

C. \(\left | \underset{AB}{\rightarrow}- \underset{DA}{\rightarrow}\right |\) = a\(\sqrt{2}\)

D. \(\left | \underset{AB}{\rightarrow}- \underset{DA}{\rightarrow}\right |\) = 2a

=> Đáp án đúng: C

Câu 14: Cho hình vuông​​ ABCD​​ cạnh​​ a, tâm​​ O.​​ Tính \(\left | \underset{OB}{\rightarrow}+ \underset{OC}{\rightarrow}\right |\)

A. \(\left | \underset{OB}{\rightarrow}+ \underset{OC}{\rightarrow}\right |\) = a

B. \(\left | \underset{OB}{\rightarrow}+ \underset{OC}{\rightarrow}\right |\) = a\(\sqrt{2}\)

C. \(\left | \underset{OB}{\rightarrow}+ \underset{OC}{\rightarrow}\right |\) = \(\dfrac {a}{2}\)

D. \(\left | \underset{OB}{\rightarrow}+ \underset{OC}{\rightarrow}\right |\) = \(\dfrac{a\sqrt{2}}{2}\)

=> Đáp án đúng: a

Câu 15: Cho tam giác​​ ABC​​ có​​ M​​ thỏa mãn điều kiện​​ \(\underset{MA}{\rightarrow}+\underset{MB}{\rightarrow}+\underset{MC}{\rightarrow}=\underset{0}{\rightarrow}\). Xác định vị trí điểm​​ M.

A. Trên đoạn AB, M là trung điểm.

B. M​​ trùng với​​ điểm C

C. Trong tam giác ABC, M là trọng tâm.

D. M​​ là điểm thứ tư của hình bình hành​​ ACBM.

=> Đáp án đúng: C

Câu 16: ABC là tam giác được cho trước.​​ Tập hợp tất cả các điểm​​ M​​ thỏa mãn đẳng thức \(\left | \underset{MB}{\rightarrow} - \underset{MC}{\rightarrow}\right |= \left | \underset{BM}{\rightarrow} - \underset{BA}{\rightarrow}\right |\) là

A. đường thẳng AB

B. trung trực đoạn BC

C. đường tròn có tâm là điểm A, bán kính R = BC

D. đường thẳng qua A và song song với BC

=> Đáp án đúng: C

Câu 17: Cho hình bình hành​​ ABCD. Tập hợp tất cả các điểm​​ M​​ thỏa mãn đẳng thức \(\underset{MA}{\rightarrow}+\underset{MB}{\rightarrow}-\underset{MC}{\rightarrow}=\underset{MD}{\rightarrow}\) là

A. một đoạn thẳng

B. một đường thẳng

C. một đường tròn

D. tập rỗng

=> Đáp án đúng: D

Câu 18: Cho tam giác​​ ABC, trong đó điểm​​ M​ đã​ thỏa mãn​​ \(\underset{MB}{\rightarrow}+\underset{MC}{\rightarrow}=\underset{AB}{\rightarrow}\). Hãy tìm vị trí điểm M trong tam giác ABC?

A. Đoạn AC có trung điểm là M

B. Trên đoạn AB, M là trung điểm.

C. Trên đoạn BC, M là trung điểm

D. M là điểm thứ 4 của hình bình hành ABCM

=> Đáp án đúng: A

Câu 19: Cho tam giác​​ ABC​​ và điểm​​ M​​ thỏa mãn điều kiện​​ \(\underset{MA}{\rightarrow}-\underset{MB}{\rightarrow}+\underset{MC}{\rightarrow}=\underset{0}{\rightarrow}\). Mệnh đề nào sai?

A. Tứ giác MABC là hình bình hành

B. \(\underset{AM}{\rightarrow}+\underset{AB}{\rightarrow}=\underset{AC}{\rightarrow}\)

C. \(\underset{BA}{\rightarrow}+\underset{BC}{\rightarrow}=\underset{BM}{\rightarrow}\)

D. \(\underset{MA}{\rightarrow}=\underset{BC}{\rightarrow}\)

=> Đáp án đúng: D

=> Đáp số đúng của đáp án D phải là \(\underset{MA}{\rightarrow}=\underset{CB}{\rightarrow}\)

Câu 20: Cho tam giác​​ ABC vuông cân tại​​ C​​ và​​ AB = \(\sqrt{2}\). Hãy tính độ dài của \(\underset{AB}{\rightarrow}+\underset{AC}{\rightarrow}\).

A. \(\underset{AB}{\rightarrow}+\underset{AC}{\rightarrow}\) = \(\sqrt{5}\)

B. \(\underset{AB}{\rightarrow}+\underset{AC}{\rightarrow}\) = 2\(\sqrt{5}\)

C. \(\underset{AB}{\rightarrow}+\underset{AC}{\rightarrow}\) = 2\(\sqrt{3}\)

D. \(\underset{AB}{\rightarrow}+\underset{AC}{\rightarrow}\) = \(\sqrt{3}\)

=> Đáp án đúng: A

Xem thêm: Tổng và hiệu của hai vectơ Bài tập SGK

Trên đây là lý thuyết tổng và hiệu của hai vectơ và bài tập tổng và hiệu của hai vectơ toán 10 mà muốn gửi đến các bạn học, mong rằng những kiến thức trên sẽ giúp ích được nhiều cho quá trình học tập của các bạn. Nếu có bất kỳ thắc mắc hay ý kiến đóng góp về bài viết các bạn hãy để lại phía bên dưới comment nhé!