Chương 3: Phân Số
Chương 3: Phân Số
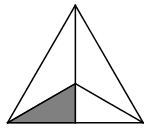
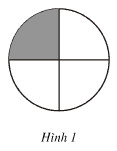
Ta biểu diễn \(\frac{1}{4}\) của hình tròn bằng cách chia hình tròn bằng 4 phần bằng nhau rồi tô màu một phần như hình 1.
Theo đó hãy biểu diễn:
a)  của hình chữ nhật (h.2) ;
của hình chữ nhật (h.2) ;

b) 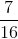 của hình vuông (h.3).
của hình vuông (h.3).
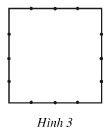
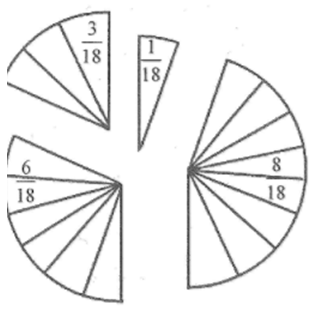
Phần tô màu trong các hình 4a, b, c, d biểu diễn phân số nào?
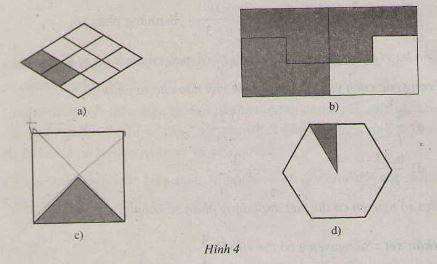
Viết các phân số sau:
a) Hai phần bảy ; b) Âm năm phần chín ;
c) Mười một phần mười ba ; c) Mười bốn phần năm.
Viết các phép chia sau dưới dạng phân số.
a) 3 : 11 ; b) -4 : 7
c) 5 : (-13) d) x chia cho 3 (x ∈ Z).
Tìm các số nguyên x và y biết :
a) \(\frac{x}{7}=\frac{6}{21}\) ;
b) \(\frac{-5}{y}=\frac{20}{28}\)
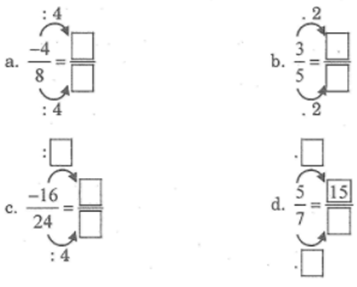
Điền số thích hợp vào ô vuông.
a) \(\frac{1}{2}=\frac{?}{12}\)
b) \(\frac{3}{4}=\frac{15}{?}\)
c) \(\frac{?}{8}=\frac{-28}{32}\)
d) \(\frac{3}{?}=\frac{12}{-24}\)
Cho hai số nguyên a và b (b ≠ 0). Chứng tỏ rằng các cặp phân số sau đây luôn bằng nhau:
a) \(\frac{a}{-b}\)và \(\frac{-a}{b}\) b) \(\frac{a}{b}\) và \(\frac{-a}{-b}\) .
Áp dụng kết quả của bài 8, hãy viết mỗi phân số sau đây thành một phân số bằng nó và có mẫu số dương:
\(\frac{3}{-4}; \frac{-5}{-7};\frac{2}{-9};\frac{-11}{-10}\)
Từ đẳng thức 2 . 3 = 1 . 6 ta có thể lập được các cặp phân số bằng nhau như sau:
\(\frac{2}{6}=\frac{1}{3};\frac{2}{1}=\frac{6}{3};\frac{3}{6}=\frac{1}{2}; \frac{3}{1}=\frac{6}{2};\frac{3.4}{.6}=\frac{6.2}{3.6}\)
Hãy lập các phân số bằng nhau từ đẳng thức 3 . 4 = 6 . 2.
Điền số thích hợp vào ô trống.
\(\frac{1}{4}=\frac{?}{?}; \frac{-3}{4}=\frac{?}{?}\)
\(1=\frac{?}{2}=\frac{?}{-4}=\frac{?}{6}=\frac{-8}{?}=\frac{10}{?}\)
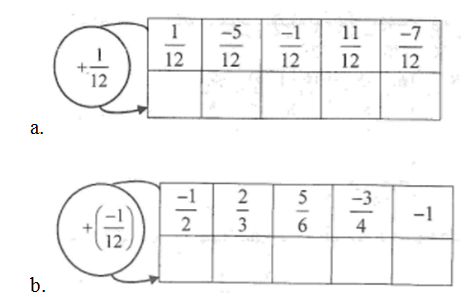
Điền số thích hợp vào ô vuông.
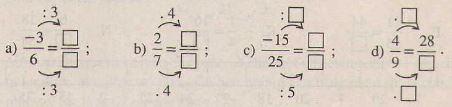
Các số sau là bao nhiêu phần của một giờ:
a) 15 phút ; b) 30 phút ; c) 45 phút ;
d) 20 phút ; e) 40 phút ; g) 10 phút ; h) 5 phút.
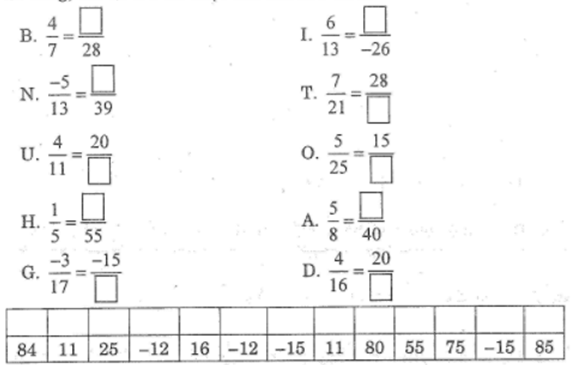
Đố : Ông đang khuyên cháu điều gì?
Điền số thích hợp vào ô trống để có hai phân số bằng nhau. Sau đó, viết các chữ tương ứng với các số tìm được vào các ô ở hai hàng dưới cùng, em sẽ trả lời được câu hỏi trên.

Rút gọn các phân số sau:
a) \(\frac{22}{55}\) ; b) \(\frac{-63}{81}\) ; c) \(\frac{20}{-140}\) ; d) \(\frac{-25}{-75}\) .
Bộ răng đầy đủ của một người trưởng thành có 32 chiếc trong đó có 8 răng cửa, 4 răng nanh, 8 răng cối nhỏ và 12 răng hàm. Hỏi mỗi loại răng chiếm mấy phần của tổng số răng (Viết dưới dạng phân số).
Rút gọn:
a) \(\frac{3.5}{8.24}\); b) \(\frac{2.14}{7.8}\) c) \(\frac{3.7.11}{22.9}\);
d) \(\frac{8.5-8.2}{16}\); e) \(\frac{11.4-11}{2-13}\).
Viết các số đo thời gian sau đây với đơn vị là giờ (chú ý rút gọn nếu có thể).
a) 20 phút b) 35 phút c) 90 phút.
Đổi ra mét vuông (viết dưới dạng phân số tối giản):
25 dm2 ; 36 dm2 ; 450 cm2 ; 575 cm2.
Tìm các cặp phân số bằng nhau trong các phân số sau đây:
\(\frac{-9}{33};\frac{15}{9};\frac{3}{-11};\frac{-12}{19};\frac{5}{3};\frac{60}{-95}\)
Trong các phân số sau đây, tìm phân số không bằng phân số nào trong các phân số còn lại:
\(\frac{-7}{42};\frac{12}{18};\frac{3}{-18};\frac{-9}{54};\frac{-10}{-15}; \frac{14}{20}\)
Điền số thích hợp vào chỗ trống:
\(\frac{2}{3}=\frac{?}{60}; \frac{3}{4}=\frac{?}{60}; \frac{4}{5}=\frac{?}{60};\frac{5}{6}=\frac{?}{60}\)
Cho tập hợp A = {0;-3;5}. Viết tập hợp B các phân số 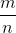 mà m, n ∈ A.
mà m, n ∈ A.
(Nếu có hai phân số bằng nhau thì chỉ cần viết một phân số).
Tìm các số nguyên x và y, biết:
\(\frac{3}{x}=\frac{y}{35}=\frac{-36}{84}\)
Viết tất cả các phân số bằng 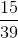 mà tử và mẫu là các số tự nhiện có hai chữ số.
mà tử và mẫu là các số tự nhiện có hai chữ số.
Cho đoạn thẳng AB:

Hãy vẽ vào vở các đoạn thẳng CD, EF, GH, IK biết rằng:
\(CD=\frac{3}{4}AB; EF=\frac{5}{6}AB;GH=\frac{1}{2}AB; IK=\frac{5}{4}AB.\)
Đố: Một học sinh đã “ rút gọn” như sau:
\(\frac{10+5}{10+10}=\frac{5}{10}=\frac{1}{2}\)
Bạn đó giải thích: “Trước hết em rút gọn cho 10, rồi rút gọn cho 5”. Đố em làm như vậy đúng hay sai? Vì sao?
a) Quy đồng mẫu các phân số sau: \(\frac{-3}{6};\frac{5}{24};\frac{-21}{56}\).
b) Trong các phân số đã cho, phân số nào chưa tối giản ?
Từ nhận xét đó, ta có thể quy đồng các phân số này như thế nào ?
Quy đồng mẫu các phân số sau:
a) \(\frac{3}{8}\) và \(\frac{5}{27}\)
b) \(\frac{-2}{9}\) và \(\frac{4}{25}\)
c) \(\frac{1}{15}\) và -6
Quy đồng mẫu các phân số sau:
a) \(\frac{{11}}{{120}}\) và \(\frac{7}{{40}}\)
b) \(\frac{{24}}{{146}}\) và \(\frac{6}{{13}}\)
c) \(\frac{7}{{30}},\frac{{13}}{{60}},\frac{{ - 9}}{{40}}\)
d) \(\frac{{17}}{{60}},\frac{{ - 5}}{{18}},\frac{{ - 64}}{{90}}\)
Hai phân số sau đây có bằng nhau không?
a) \(\frac{{ - 5}}{{14}}\) và \(\frac{{30}}{{ - 84}}\)
b) \(\frac{{ - 6}}{{102}}\) và \(\frac{{ - 9}}{{153}}\)
Quy đồng mẫu các phân số:
a) \(\frac{{ - 4}}{7};\frac{8}{9};\frac{{10}}{{21}}\)
b) \(\frac{5}{{{2^2}.3}};\frac{7}{{{2^2}.11}}\)
Quy đồng mẫu các phân số:
a) \(\frac{{ - 3}}{{20}};\frac{{ - 11}}{{ - 30}};\frac{7}{{15}}\)
b) \(\frac{{ - 6}}{{ - 35}};\frac{{ - 27}}{{ - 180}};\frac{{ - 3}}{{ - 28}}\)
Hai phân số sau đây có bằng nhau không?
a) \(\frac{{ - 5}}{{14}}\) và \(\frac{{30}}{{ - 84}}\)
b) \(\frac{{ - 6}}{{102}}\) và \(\frac{{-9}}{{ 153}}\)
Quy đồng mẫu các phân số:
a. \(\frac{{ - 4}}{7},\frac{8}{9},\frac{{ - 10}}{{21}}\) b,\(\frac{5}{{{2^2}.3}},\frac{7}{{{2^3}.11}}\)
Quy đồng mẫu các phân số:
a. \(\frac{3}{{ - 20}},\frac{{ - 11}}{{ - 30}},\frac{7}{{15}}\) b.\(\frac{{ - 6}}{{ - 35}},\frac{{27}}{{ - 180}}\)
Quy đồng mẫu các phân số:
a. \(\frac{{ - 5}}{5},\frac{8}{7}\) b.\(3,\frac{{ - 3}}{5},\frac{{ - 5}}{6}\) c.\(\frac{{ - 9}}{7},\frac{{ - 19}}{{15}}, - 1\)
Rút gọn rồi quy đồng mẫu các phân số:
a, \(\frac{{ - 15}}{{90}};\frac{{120}}{{600}};\frac{{ - 75}}{{150}}\)
b,\(\frac{{54}}{{ - 90}};\frac{{ - 180}}{{288}};\frac{{60}}{{ - 135}}\)
Đố vui: Hai bức ảnh dưới đây chụp di tích nào?
.png)
Cho các dãy phân số sau:
N.\(\frac{1}{4},\frac{3}{{10}},\frac{2}{5},...\) M.\(\frac{2}{3},\frac{3}{4},\frac{5}{6}\),…
H.\[\frac{1}{6},\frac{1}{4},\frac{1}{3}\] ,… S.\[\frac{2}{9},\frac{5}{{18}},\frac{1}{3}\],…
Y.\[\frac{1}{{20}},\frac{1}{8},\frac{1}{5}\] ,… A \[\frac{1}{7},\frac{5}{{14}},\frac{4}{7}\] ,…
O. \[\frac{1}{{20}},\frac{1}{8},\frac{1}{5}\] ,… I. \(\frac{1}{{18}},\frac{2}{9},\frac{7}{{18}}\)
Hãy quy đồng mẫu các phân số của từng dãy rồi đoán nhận phận số thứ tư của dãy đó; viết nó dưới dạng tối giản rồi viết chữ cái ở dãy đó vào ô tương ứng với phân số ấy ở hình 6. Khi đó, em sẽ biết được hai địa danh của Việt Nam được UNESCO công nhận là di sản văn hóa thế giới vào năm 1999.
Chẳng hạn, ở dãy đầu có ghi chữ N, quy đồng mẫu ta được \(\frac{2}{{10}},\frac{3}{{10}},\frac{4}{{10}}\) nên phân số thứ tư là \(\frac{5}{{10}}\) . Nó có dạng tối giản \(\frac{1}{2}\), do đó ta điền chữ N vào hai ô ứng với số \(\frac{1}{2}\)trên hình 6.
.png)
Điền số thích hợp vào chỗ trống:
a) \(\frac{{ - 11}}{{13}} < \frac{{...}}{{13}} < \frac{{...}}{{13}} < \frac{{...}}{{13}} < \frac{{ - 7}}{{13}}\)
b) \(\frac{{ - 1}}{3} < \frac{{...}}{{36}} < \frac{{...}}{{18}} < \frac{{..1}}{4}\)
a) Thời gian nào dài hơn: \(\frac{2}{3}h\,\,hay\,\,\frac{3}{4}h?\)
b) Đoạn thẳng nào ngắn hơn: \(\frac{7}{{10}}m\,\,hay\,\,\frac{3}{4}m?\)
c) Khối lượng nào lớn hơn: \(\frac{7}{8}kg\,\,hay\,\,\frac{9}{{10}}kg?\)
d) Vận tốc nào nhỏ hơn: \[\frac{5}{6}km/h\,\,hay\,\frac{7}{9}km/h?\]
Lớp 6B có \(\frac{4}{5}\) số học sinh thích bóng bàn, \(\frac{7}{{10}}\) số học sinh thích bóng chuyền, \(\frac{{23}}{{25}}\) số học sinh thích bóng đá. Môn bóng nào được nhiều bạn học sinh lớp 6B yêu thích nhất ?
Lưới nào sẫm nhất?
a) Đối với mỗi lưới ô vuông hình 7, hãy lập một phân số có tử số là ô đen, mẫu số là tổng số ô đen và ô trắng.
.jpg)
b) Sắp xếp các phân số này theo thứ tự tăng dần và cho biết lưới nào sẫm nhất (có tỉ số ô đen so với tổng số ô là lớn nhất.
Đối với phân số ta có tính chất : Nếu \(\frac{a}{b} > \frac{c}{d}\) và \(\frac{c}{d} > \frac{p}{q}\) thì \(\frac{a}{b} > \frac{p}{q}\)
Dựa vào tính chất này, hãy so sánh:
a) \(\frac{6}{7}\) và \(\frac{{11}}{{10}}\)
b) \(\frac{{ - 5}}{{17}}\) và \(\frac{2}{7}\)
c) \(\frac{{419}}{{ - 723}}\) và \(\frac{{ - 697}}{{ - 313}}\)
Cộng các phân số (rút gọn nếu có thể).
a) \(\frac{7}{{ - 25}} + \frac{{ - 8}}{{25}}\) b) \(\frac{1}{6} + \frac{{ - 5}}{6}\)
c) \(\frac{6}{{13}} + \frac{{ - 14}}{{39}}\) c) \(\frac{4}{5} + \frac{4}{{ - 18}}\)
Điền dấu thích hợp (<, >, = ) vào ô vuông.
.jpg)
Cho \(x=\frac{1}{2}+\frac{-2}{3}\). Hỏi giá trị của x là số nào trong các số sau.
a) \(\frac{-1}{5}\) ; b) \(\frac{1}{5}\) ; c) \(\frac{-1}{6}\) ; d) \(\frac{1}{6}\) ; e) \(\frac{7}{6}\) ?
Tính nhanh.
a) \(\frac{-3}{7}+\frac{5}{13}+\frac{-4}{7}\) ;
b) \(\frac{-5}{21}+\frac{-2}{21}+\frac{8}{24}\) .
Đố : Cắt một tấm bìa hình tròn bán kính 2,5cm thành 4 phần không bằng nhau như hình 8.
.png)
Đố em đặt các miếng bìa đã cắt cạnh nhau để được:
a) \(\frac{1}{4}\) hình tròn ;
b) \(\frac{1}{2}\) hinh tròn ;
c) \(\frac{7}{12},\frac{2}{3},\frac{3}{4},\frac{5}{6},\frac{11}{12}\) và \(\frac{12}{12}\) hình tròn.
Hùng đi xe đạp, 10 phút đầu đi được \(\frac{1}{3}\) quãng đường, 10 phút thứ hai đi được \(\frac{1}{4}\) quãng đường, 10 phút cuối cùng đi được \(\frac{2}{9}\) quãng đường. Hỏi sau 30 phút Hùng đi được bao nhiêu phần quãng đường ?
Điền số thích hợp vào ô trống ở bảng dưới:
.png)
Tìm năm cách chọn ba trong bảy số sau đây để khi cộng lại được tổng là 0:
\(\frac{-1}{6},\frac{-1}{3},\frac{-1}{2},0, \frac{1}{2},\frac{1}{3};\frac{1}{6}.\)
Ví dụ. \(\frac{-1}{2}+\frac{1}{3}+\frac{1}{6}=0.\)
Điền số thích hợp vào ô trống:
|
a |
\({6 \over {27}}\) |
\({3 \over 5}\) |
\({5 \over {14}}\) |
\({4 \over 3}\) |
\({2 \over 5}\) |
|
|
b |
\({5 \over 7}\) |
\({4 \over {23}}\) |
\({7 \over {10}}\) |
\({2 \over 7}\) |
\({2 \over 3}\) |
|
|
a + b |
\({{11} \over {23}}\) |
\({8 \over 5}\) |
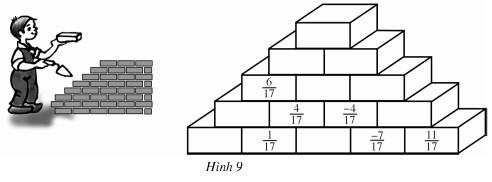
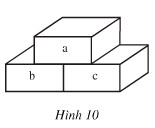
“Xây trường”
Em hãy “xây bức tường” ở hình 9 này bằng cách điền các phân số thích hợp vào các “viên gạch” theo quy tắc sau:
a = b + c (h.10).
Trong vở bài tập của bạn An có bài làm sau:
a) \({{ - 3} \over 5} + {1 \over 5} = {4 \over 5}\)
b) \({{ - 10} \over {13}} + {{ - 2} \over {13}} = {{ - 12} \over {13}}\)
c) \({2 \over 3} + {{ - 1} \over 6} = {4 \over 6} + {{ - 1} \over 6} = {3 \over 6} = {1 \over 2}\)
d) \({{ - 2} \over 3} + {2 \over { - 5}} = {{ - 2} \over 3} + {{ - 2} \over 5} = {{ - 10} \over {15}} + {{ - 6} \over {15}} = {{ - 4} \over {15}}\)
Hãy kiểm tra lại các đáp số và sửa lại chỗ sai (nếu có).
Điền số thích hợp vào ô trống. Chú ý rút gọn kết quả (nếu có thể):
|
+ |
\({{ - 1} \over 2}\) |
\({5 \over 9}\) |
\({1 \over {36}}\) |
\({{ - 11} \over {18}}\) |
|
\({{ - 1} \over 2}\) |
- 1 |
|
|
|
|
\({5 \over 9}\) |
|
|
|
|
|
\({1 \over {36}}\) |
|
|
|
|
|
\({{ - 11} \over {18}}\) |
|
|
|
|
Tính nhanh giá trị của các biểu thức sau:
\(A = {{ - 5} \over {11}} + \left( {{{ - 6} \over {11}} + 1} \right)\)
\(B = {2 \over 3} + \left( {{5 \over 7} + {{ - 2} \over 3}} \right)\)
\(C = \left( {{{ - 1} \over 4} + {5 \over 8}} \right) + {{ - 3} \over 8}\)
Trong các câu sau đây, hãy chọn một câu đúng:
Muốn cộng hai phân số \({{ - 3} \over 4}\) và \({4 \over 5}\) ta làm như sau:
a) Cộng tử với tử, cộng mẫu với mẫu.
b) Nhận mẫu của phân số \({{ - 3} \over 4}\) với 5, nhân mẫu của phân số \({4 \over 5}\) với 4 rồi cộng hai tử lại.
c) Nhân cả tử lẫn mẫu của phân số \({{ - 3} \over 4}\) với 5, nhân cả tử lẫn mẫu của phân số \({4 \over 5}\) với 4 rồi cộng hai tử mới lại , giữ nguyên mẫu chung.
d) Nhân cả tử lẫn mẫu của phân số \({{ - 3} \over 4}\) với 5, nhận cả tử lẫn mẫu của phân số \({4 \over 5}\) với 4 rồi cộng tử với tử, mẫu với mẫu.
Tìm số đối của các số:
\(\frac{2}{3}\) , -7 , \(\frac{-3}{5}\) , \(\frac{-4}{7}\) , \(\frac{6}{11}\) , 0 , 112.
Tính:
a) \(\frac{1}{8}-\frac{1}{2}\) ; b) \(\frac{-11}{12}-(-1)\) ; c) \(\frac{3}{5}-\frac{5}{6}\) ;
d) \(\frac{-1}{16}-\frac{1}{15}\) e) \(\frac{11}{36}-\frac{-7}{24}\) ; g) \(\frac{-5}{9}-\frac{-5}{12}\) .
Tìm x, biết:
a) \(x - \frac{3}{4}=\frac{1}{2}\) ;
b) \(\frac{-5}{6}-x=\frac{7}{12}+\frac{-1}{3}\) ;
Trong hai câu sau đây có một câu đúng, một câu sai:
Câu thứ nhất : Tổng của hai phân số là một phân số có tử bằng tổng các tử, mẫu bằng tổng các mẫu.
Câu thứ hai : Tổng của hai phân số có cùng mẫu số là một phân số có cùng mẫu số đó và có tử bằng tổng các tử.
a) Câu nào là câu đúng?
b)Theo mẫu của câu đúng, hãy phát biểu tương tự cho hiệu của hai phân số cùng mẫu số.
Một khu đất hình chữ nhật có chiều dài là \(\frac{3}{4}\) km, chiều rộng là \(\frac{5}{8}\)km.
a) Tính nửa chu vi của khu đất (tính bằng km)
b) Chiều dài hơn chiều rộng bao nhiêu kilômet ?
Điền phân số thích hợp vào ô vuông:

Hoàn thành các phép tính:
a) \({7 \over 9} - { \ldots \over 3} = {1 \over 9}\)
b) \({1 \over \ldots } - {{ - 2} \over {15}} = {7 \over {15}}\)
c) \({{ - 11} \over {14}} - {{ - 4} \over \ldots } = {{ - 3} \over {14}}\)
d) \({ \ldots \over {21}} - {2 \over 3} = {5 \over {21}}\)
Buổi tối (từ 19 giờ đến 21 giờ 30 phút), Bình Định dành \({1 \over 4}\) giờ để rửa bát, \({1 \over 6}\) giờ để quét nhà và 1 giờ để làm bài tập.Thời gian còn lại, Bình Định dành để xem chương trình phim truyện truyền hình kéo dài 45 phút. Hỏi Bình Định có đủ thời gian để xem hết phim không?
Điền số thích hợp vào ô trống:
|
\({a \over b}\) |
\({{ - 3} \over 4}\) |
|
|
0 |
Dòng 1 |
|
\( - {a \over b}\) |
|
\({{ - 4} \over 5}\) |
|
|
Dòng 2 |
|
\( - \left( { - {a \over b}} \right)\) |
|
|
\({{ - 7} \over {11}}\) |
|
Dòng 3 |
So sánh dòng 1 và dòng 3, em có thể nói gì về “số đối của số đối của một số”?
Trong một dãy tính chỉ có phép cộng và phép trừ phân số, ta thực hiện phép tính theo thứ tự từ trái sang phải.
Tính: \({2 \over 9} + {5 \over { - 12}} - {3 \over 4}\)
Điền số thích hợp và chỗ trống để hoành thành phép tính:
\({2 \over 9} + {5 \over { - 12}} - {{ - 3} \over 9} = {2 \over 9} + {{ - 5} \over {12}} + {3 \over 4} = {{2.4} \over {36}} + {{\left( { - 5} \right). \ldots } \over {36}} + {{3. \ldots } \over {36}} = {{8 - \ldots + \ldots } \over {36}} = {{20} \over {36}} = { \ldots \over \ldots }\)
Tính:
a) \({3 \over 5} - {7 \over {10}} - {{13} \over { - 20}}\)
b) \({3 \over 4} + {{ - 1} \over 3} = {5 \over {18}}\)
c) \({3 \over {14}} - {5 \over { - 8}} + {{ - 1} \over 2}\)
d) \({1 \over 2} + {1 \over { - 3}} + {1 \over 4} - {{ - 1} \over 6}\)
Nhân các phân số (rút gọn nếu có thể):
a) \(\frac{-1}{4}.\frac{1}{3}\) ; b) \(\frac{-2}{5}.\frac{5}{-9}\) ; c) \(\frac{-3}{4}.\frac{16}{7}\) ;
d) \(\frac{-8}{3}.\frac{15}{24}\) ; e) \((-5).\frac{8}{15}\) ; g) \(\frac{-9}{11}.\frac{5}{18}\) .
Phân số \(\frac{6}{35}\) có thể được viết dưới dạng tích của hai phân số có tử và mẫu số là số nguyên dương có một chữ số.
Chẳng hạn: \(\frac{6}{35}=\frac{2}{5}.\frac{3}{7}\). Hãy tìm cách viết khác.
Tìm x, biết:
a) \(x-\frac{1}{4}=\frac{5}{8}.\frac{2}{3}\) ;
b) \(\frac{x}{126}=\frac{-5}{9}.\frac{4}{7}\) ;
Đố: Có những cặp phân số mà khi ta nhân chúng với nhau hoặc cộng chúng với nhau đều được cùng một kết quả.
Chẳng hạn : Cặp phân số \(\frac{7}{3}\) và \(\frac{7}{4}\) có :
\(\frac{7}{3}.\frac{7}{4}=\frac{7.7}{3.4}=\frac{49}{12}\)
\(\frac{7}{3}+\frac{7}{4}=\frac{7.4+7.3}{3.4}=\frac{49}{12}\).
Đố em tìm được một cặp phân số khác cũng có tính chất ấy.
Trong hai câu sau đây, câu nào đúng ?
Câu thứ nhất: Để nhân hai phân số cùng mẫu, ta nhân hai tử với nhau và giữ nguyên mẫu.
Câu thứ hai: Tích của hai phân số bất kì là một phân số có tử là tích của hai tử và mẫu là tích của hai mẫu.
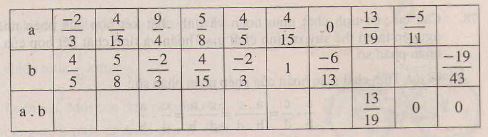
Điền các số thích hợp vào bảng sau:
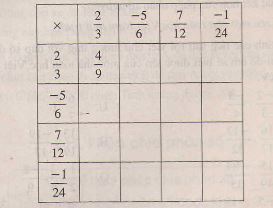
Hoàn thành bảng nhân sau (chú ý rút ngắn gọn nếu có thể) :
Tính giá trị biểu thức sau một cách hợp lí:
\(A=\frac{7}{19}.\frac{8}{11}+\frac{7}{19}.\frac{3}{11}+\frac{12}{19}\) ;
\(B= \frac{5}{9}.\frac{7}{13}+\frac{5}{9}.\frac{9}{13}-\frac{5}{9}.\frac{3}{13}\) ;
\(C=\left (\frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right ).\left (\frac{1}{3}-\frac{1}{4}-\frac{1}{12} \right )\).
Tính giá trị các biểu thức sau:
\(A=a.\frac{1}{2} +a.\frac{1}{3}-a.\frac{1}{4}\) với \(a= \frac{-4}{5}\);
\(B=\frac{3}{4}.b+\frac{4}{3}.b-\frac{1}{2}.b\) với \(b=\frac{16}{9}\) ;
\(C=c.\frac{3}{4}+c.\frac{5}{6}-c.\frac{19}{12}\) với \(c=\frac{2002}{2003}\) ;
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số.
Ví dụ. Tính chất giao hoán của phép nhân phân số:
\({a \over b}.{c \over d} = {{a.c} \over {b.d}} = {{c.a} \over {d.b}} = {c \over d}.{a \over b}\)
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên .
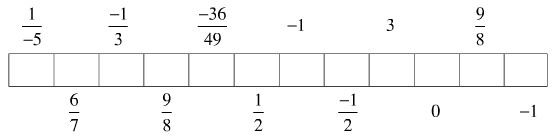
Em hãy tính các tích sau rồi viết chữ tương ứng với đáp số đúng vào các ô trống. Khi đó em sẽ biết được tên của một nhà toán học Việt Nam nổi tiếng ở thế kỉ XV.
T. \({{ - 2} \over 3}.{{ - 3} \over 4}\) U. \({6 \over 7}.1\)
E. \({{16} \over {17}}.{{ - 17} \over {32}}\) H. \({{13} \over {19}}.{{ - 19} \over {13}}\)
G. \({{15} \over {49}}.{{ - 84} \over {35}}\) O. \({1 \over 2}.{3 \over 4}.{{ - 8} \over 9}\)
N. \({{ - 5} \over {16}}.{{ - 18} \over 5}\) I.\({6 \over {11}}.{{ - 1} \over 7}.0.{3 \over {29}}\)
V. \({7 \over 6}.{{36} \over {14}}\) L. \({3 \over { - 5}}.{1 \over 3}\)
Tính:
a) \(5.{{ - 3} \over {10}}\) b) \({2 \over 7} + {5 \over 7}.{{14} \over {25}}\)
c) \({1 \over 3} - {5 \over 4}.{4 \over {15}}\) d) \(\left( {{3 \over 4} + {{ - 7} \over 2}} \right).\left( {{2 \over {11}} + {{12} \over {22}}} \right)\)
Tính diện tích và chu vi một khu đất hình chữ nhật có chiều dài 1/4km và chiều rộng 1/8km
Toán vui. Một con ong và bạn Dũng cùng xuất phát từ A đến B. Biết rằng mỗi giây ong bay đươc 5m và mỗi giờ Dũng đạp xe đi được 12 km. Hỏi con ong hay bạn Dũng đến B trước?
Lúc 6 giờ 50 phút bạn Việt đi xe đạp từ A để đến B với vận tốc 15 km/h. Lúc 7 giờ 10 phút bạn Nam đi xe đạp từ A đến B với vận tốc 15 km/h. Hai bạn gặp nhau ở C lúc 7 giờ 30 phút. Tính quãng đường AB.
Tính:
a) \(\frac{-5}{6}:\frac{3}{13}\) ; b) \(\frac{-4}{7}:\frac{-1}{11}\) ; c) \(-15:\frac{3}{2}\) ;
d) \(\frac{9}{5}:\frac{-3}{5}\) ; e) \(\frac{5}{9}:\frac{5}{-3}\) ; g) \(0:\frac{-7}{11}\) ;
h) \(\frac{3}{4}:(-9)\).
Phân số \(\frac{6}{35}\) có thể viết dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có một chữ số.
Chẳng hạn: \(\frac{6}{35}=\frac{2}{5}.\frac{3}{7}=\frac{2}{5}:\frac{7}{3}\) . Em hãy tìm ít nhất một cách viết khác.
Tìm x, biết:
a) \(\frac{4}{5}.x=\frac{4}{7};\)
b) \(\frac{3}{4}:x=\frac{1}{2}\).
a) Hãy tính giá trị của biểu thức sau:
\(\frac{2}{7}:1\) ; \(\frac{2}{7}:\frac{3}{4}\) ; \(\frac{2}{7}:\frac{5}{4}\).
b) So sánh số chia với 1 trong mỗi trường hợp
c) So sánh giá trị tìm được với số bị chia rồi rút ra kết luận.
Một tấm bìa hình chữ nhật có diện tích là \(\frac{2}{7}\)m2, chiều dài là \(\frac{2}{3}\)m, tính chu vi của tấm bìa đó.
Thực hiện phép chia:
\({{ - 4} \over {13}}:2\)
\(24:{{ - 6} \over {11}}\)
\({9 \over {34}}:{3 \over {17}}\)
Tìm x, biết:
a) \(x.{3 \over 7} = {2 \over 3}\) d) \({4 \over 7}.x - {2 \over 3} = {1 \over 5}\)
b) \(x:{8 \over {11}} = {{11} \over 3}\) e) \({2 \over 9} - {7 \over 8}.x = {1 \over 3}\)
c) \({2 \over 5}:x = {{ - 1} \over 4}\) g) \({4 \over 5} + {5 \over 7}:x = {1 \over 6}\)
Người ta đóng 225 lít nước khoáng vào loại chai \({3 \over 4}\) lít. Hỏi đóng được tất cả bao nhiêu chai?
Minh đi xe đạp từ nhà đến trường với vận tốc 10 km/h hết \({1 \over 5}\) giờ. Khi về, Minh đạp xe với vận tốc 12 km/h. Tính thời gian Minh đi từ trường về nhà.
Tính:
a) \({4 \over 7}:\left( {{2 \over 5}.{4 \over 7}} \right)\)
b) \({6 \over 7} + {5 \over 7}:5 - {8 \over 9}\)
Viết các phân số sau dưới dạng hỗn số:
\(\frac{6}{5}\) , \(\frac{7}{3}\) , \(\frac{-16}{11}\);
Viết các hỗn số sau dưới dạng phân số:
\(5\tfrac{1}{7}\) , \(6\tfrac{3}{4}\) , \(-1\tfrac{12}{13}\) .
So sánh các phân số:
\(\frac{22}{7}\) và \(\frac{34}{11}\) .
Đổi ra mét (viết kết quả dưới dạng phân số thập phân rồi dưới dạng số thập phân).
3dm , 85cm , 52mm.
Dùng phần trăm với kí hiệu % để viết các số phần trăm trong các câu sau đây:
Để đạt tiêu chuẩn công nhận phổ cập giáo dục THCS, xã Bình Minh đã đề ra chỉ tiêu phấn đấu:
- Huy động số trẻ 6 tuổi đi học lớp 1 đạt chín mươi mốt phần trăm. Có ít nhất tám mươi hai phần trăm số trẻ ở độ tuổi 11 - 14 tốt nghiệp Tiểu học ;
- Huy động chín mươi sáu phần trăm học sinh tốt nghiệp Tiểu học hàng năm vào lớp 6 THCS phổ thông và THCS bổ túc;
- Bảo đảm tỉ lệ học sinh tốt nghiệp THCS hàng năm từ chín mươi tư phần trăm trở lên.
Khi cộng hai hỗn số \(3{1 \over 5};2{2 \over 3}\) bạn Cường làm như sau:
\(3{1 \over 5} + 2{2 \over 3} = {{16} \over 5} + {8 \over 3} = {{48} \over {15}} + {{40} \over {15}} = {{88} \over {15}} = 5{{13} \over {15}}\)
a) Bạn Cường đã tiến hành cộng hai hỗn số như thế nào?
b) Có cách nào tính nhanh hơn không?
Tính giá trị của các biểu thức sau:
\(A = 8{2 \over 7} - \left( {3{4 \over 9} + 4{2 \over 7}} \right)\)
\(B = \left( {10{2 \over 9} + 2{3 \over 5}} \right) - 6{2 \over 9}\)
Thực hiện phép nhân hoặc phép chia hai hỗn số bằng cách viết hỗn số dưới dạng phân số:
a) \(5{1 \over 2}.3{3 \over 4}\)
b) \(6{1 \over 3}:4{2 \over 9}\)
Bạn Hoàng làm phép nhân \(4{3 \over 7}.2\) như sau:
\(4{3 \over 7}.2 = {{31} \over 7}.2 = {{31} \over 7}.{2 \over 1} = {{62} \over 7} = 8{6 \over 7}\).
Có cách nào tính nhanh hơn không? Nếu có, hãy giải thích cách làm đó.
a) Khi chia một số cho 0,5 ta chỉ việc nhân số đó với 2.
Ví dụ: 37 : 0,5 = 37 . 2 = 74;
102: 0,5 = 102 . 2 = 204.
Hãy giải thích tại sao lại làm như vậy?
b) Hãy tìm hiểu cách làm tương tự khi chia một số cho 0,25; cho 0,125. Cho các ví dụ minh họa.
Viết các phân số sau dưới dạng số thập phân và đúng kí hiệu %:
\({7 \over {25}},{{19} \over 4},{{26} \over {65}}\)
Viết các phần trăm sau dưới dạng số thập phân:
7%, 45%, 216%
Hoàn thành các phép tính sau:
\({7 \over 9} + {5 \over {12}} - {3 \over 4} = {{7.4} \over {36}} + {{5. \ldots } \over {36}} - {{3. \ldots } \over {36}} = {{28 + \ldots - \ldots } \over {36}} = {{16} \over {36}} = { \ldots \over \ldots }\)
Tính:
a) \({1 \over 3} + {3 \over 8} - {7 \over {12}}\)
b) \({{ - 3} \over {14}} + {5 \over 8} - {1 \over 2}\)
c) \({1 \over 4} - {2 \over 3} - {{11} \over {18}}\)
d) \({1 \over 4} + {5 \over {12}} - {1 \over {13}} - {7 \over 8}\)
Hoàn thiện các phép tính sau:
a) Tính tổng: \(1{3 \over 4} + 3{5 \over 9}\)
Cách 1:
\(1{3 \over 4} + 3{5 \over 9} = { \ldots \over 4} + { \ldots \over 9} = {{63} \over {36}} + { \ldots \over {36}} = { \ldots \over {36}} = \ldots \)
Cách 2:
\(1{3 \over 4} + 3{5 \over 9} = 1{ \ldots \over {36}} + 3{ \ldots \over {36}} = 4{ \ldots \over {36}} = 5{ \ldots \over {36}}\)
b) Tínhhiệu: \(3{5 \over 6} - 1{9 \over {10}}\)
Cách 1:
\(3{5 \over 6} - 1{9 \over {10}} = {{23} \over 6} - { \ldots \over \ldots } = {{...} \over {30}} - {{...} \over {30}} = {{58} \over {30}} = \ldots \)
Cách 2:
\(3{5 \over 6} - 1{9 \over {10}} = 3{{25} \over {30}} - 1{{27} \over {30}} = 2{{55} \over {30}} - 1{ \ldots \over {30}} = \ldots {{...} \over {...}} = 1{ \ldots \over {15}}\)
Tính bằng hai cách:
a) \(2{4 \over 9} + 1{1 \over 6}\)
b) \(7{1 \over 8} - 5{3 \over 4}\)
c) \(4 - 2{6 \over 7}\)
Áp dụng tính chất các phép tính và quy tắc dấu ngoặc để tính giá trị các biểu thức sau:
\(A = 11{3 \over {13}} - \left( {2{4 \over 7} + 5{3 \over {13}}} \right)\)
\(B = \left( {6{4 \over 9} + 3{7 \over {11}}} \right) - 4{4 \over 9}\)
\(C = {{ - 5} \over 7}.{2 \over {11}} + {{ - 5} \over 7}.{9 \over {11}} + 1{5 \over 7}\)
\(D = 0,7.2{2 \over 3}.20.0,365.{5 \over {28}}\)
\(E = \left( { - 6,17 + 3{5 \over 9} - 2{{36} \over {97}}} \right).\left( {{1 \over 3} - 0,25 - {1 \over {12}}} \right)\)
Tìm số nghịch đảo của các số sau:
\({3 \over 7},6{1 \over 3},{{ - 1} \over {12}},0,31\)
Hãy kiểm tra các phép cộng sau đây rồi sử dụng kết quả của các phép cộng này để điền số thích hợp vào ô trống mà không cần tính toán:

|
(36,05+ 2678,2) + 126 = |
|
|
|
(126 + 36,05) + 13,214 = |
|
|
|
(678,27 + 14,02) + 2819,1 = |
|
|
|
3497,37 – 678,27 = |
|
Hãy kiểm tra các phép nhân sau đây rồi sử dụng kết quả của các phép nhân này để điền số thích hợp vào ô trống mà không cần tính toán:
a) 39 . 47 = 1833;
b)15,6 . 7,02 = 109,512;
c)1833 . 3,1 = 5682,3;
d)109,512 . 5,2 = 569,4624.
|
(3,1 . 47) . 39 = |
|
|
|
(15,6 . 5,2) . 7,02 = |
|
|
|
5682,3 : (3,1 . 47) = |
|
Tìm:
a) \({2 \over 3}\) của 8,7 ; b) \({2 \over 7}\) của \({-11 \over 6}\) ;
c) \(2{1 \over 3}\) của 5,1 ; d) \(2{7 \over {11}}\) của \(6{3 \over 5}\).
Hãy so sánh 16% của 25 và 25% của 16. Dựa vào nhận xét đó hãy tính nhanh.
a) 84% của 25 ; b) 48% của 50.
Biết rằng 13,21 . 3 = 39,63 và 39,63 : 5 = 7,926. Hãy tìm \(\frac{3}{5}\) của 13,21 và \(\frac{5}{3}\) của 7,926 mà không cần tính toán.
Tuấn có 21 viên bi. Tuấn cho Dũng \(\frac{3}{7}\) số bi của mình. Hỏi
a) Dũng được Tuấn cho bao nhiêu viên bi ?
b) Tuấn còn lại bao nhiêu viên bi ?
Đố: An nói :" Lấy một phần hai của một phần hai rồi đem chia cho một phần hai sẽ được kết quả là một phần hai". Đố em bạn An nói có đúng không?
Sử dụng máy tính bỏ túi.
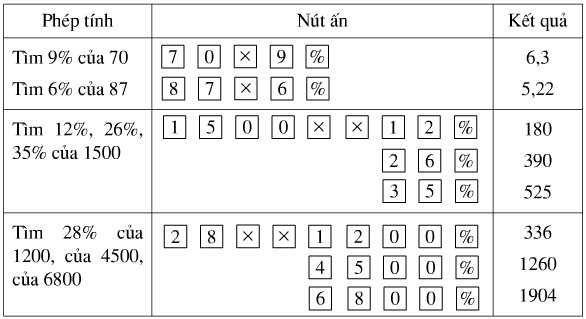
Sử dụng máy tính bỏ túi để tính :
a) 3,7% của 13,5 ; b) 6,5% của 52,61 ;
c) 17% . 29% của 2534 ; d) 48% của 264, 395, 1836.
Đoạn đường sắt Hà Nội – Hải Phòng dài 102 km. Một xe lửa xuất phát từ Hà Nội đã đi được \({3 \over 5}\) quãng đường. Hỏi xe lửa còn cách Hải Phòng bao nhiêu Kilomet ?
Nguyên liệu để muối dưa cải gồm rau cải, hành tươi, đường và muối. Khối lượng hành, đường muối theo thứ tự bằng 5%, \({1 \over {1000}}\) và \({3 \over {40}}\) khối lượng rau cải. Vậy nếu muối 2 kg rau cải thì cần bao nhiêu ki lô gam hành, đường và muối?
Nhân dịp lễ Quốc Khánh 2 – 9, một cửa hàng giảm giá 10% một số mặt hàng. Người bán hàng đã sửa lại giá của các mặt hàng ấy như sau:

Em hãy kiểm tra xem người bán hàng tính giá mới có đúng không?
Sử dụng máy tính bỏ túi
Ví dụ: Một quyển sách giá 8000đ. Tìm giá mới của quyển sách sau khi giảm giá 15%.
Vậy giá mới của quyển sách là 6800đ.
Theo cách trên, em hãy dùng máy tính bỏ túi để kiểm tra giá mới của các mặt hàng nêu ở bài tập 123.
Bố bạn Lan gửi tiết kiệm 1 triệu đồng tại một ngân hàng theo thể thức “có kì hạn 12 tháng” với lãi suất 0,58% một tháng (tiền lãi một tháng bằng 0,58% số tiền gửi ban đầu và sau 12 tháng mới được lấy lãi). Hỏi hết thời hạn 12 tháng ấy, bố bạn lấy ra cả vốn lẫn lãi được bao nhiêu?
Tìm một số biết :
a) \(\frac{2}{3}\) của nó bằng 7,2 ;
b) \(1\frac{3}{7}\) của nó bằng -5.
Biết rằng 13,32 . 7 = 93,24 và 93,24 : 3 = 31,08. Không cần làm phép tính, hãy :
a) Tìm một số, biết \(\frac{3}{7}\) của nó bằng 13,32 ;
b) Tìm một số, biết \(\frac{7}{3}\) của nó bằng 31,08.
Trong đậu đen nấu chín, tỉ lệ chất đạm chiếm 24%. Tính số kilôgam đậu đen đã nấu chín để có 1,2kg chất đạm.
Trong sữa có 4,5% bơ. Tính lượng sữa trong một chai biết rằng lượng bơ trong chai sữa này là 18g.
Đố: Đố em tìm được một số mà một nửa số đó bằng \(\frac{1}{3}\) ?
75% một mảnh vải dài 3,75m. Hỏi cả mảnh vải dài bao nhiêu mét?
Tìm x, biết:
a) \(2{2 \over 3}.x + 8{2 \over 3} = 3{1 \over 3}\)
b) \(3{2 \over 7}.x - {1 \over 8} = 2{3 \over 4}\)
Để làm món “Dừa kho thịt”, ta cần có cùi dừa (cơm dừa), thịt ba chỉ, đường, nước mắm, muối. Lượng thịt ba chỉ và lượng đường theo thứ tự bằng \({2 \over 3}\) và 5% lượng cùi dừa. Nếu có 0,8 kg thịt ba chỉ thì phải cần bao nhiêu ki lô gam cùi dừa. Nếu có 0,8 kg thịt ba chỉ thì phải cần bao nhiêu ki lô gam cùi dừa, bao nhiêu ki lô gam đường?
Sử dụng máy tính bỏ túi
Vậy số phải tìm là 30.
Hãy dùng máy tính bỏ túi, kiểm tra lại đáp số của các bài tập 128, 129, 131.
Một xí nghiệp đã thực hiện \({5 \over 9}\) kế hoạch, còn phải làm tiêp 560 sản phẩm nữa mới hoàn thành kế hoạch. Tính số sản phẩm xí nghiệp được giao theo kế hoạch.
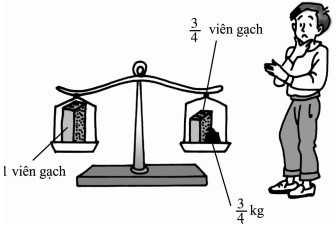
Đố (Theo một bài toán của Xem Lôi – đơ (Sam Loyd)) : Trong hình 11, cân đang ở vị trí thăng bằng. Đố em viên gạch nặng bao nhiêu ki lô gam ?
Tìm tỉ số của:
a) \(\frac{2}{3}\)m và 75cm;
b) \(\frac{3}{10}\)h và 20 phút.
Ta có thể đưa tỉ số của hai số về tỉ số của hai số nguyên.
Chẳng hạn, tỉ số của hai số 0,75 và \(1\frac{7}{20}\) có thể viết như sau:
\(\frac{0,75}{1\frac{7}{20}}=\frac{\frac{75}{100}}{\frac{27}{20}}=\frac{75}{100}.\frac{20}{27}=\frac{5}{9}.\)
Hãy viết các tỉ số sau đây thành tỉ số của hai số nguyên:
a) \(\frac{1,28}{3,15}\) ; b) \(\frac{2}{5}:3\frac{1}{4}\) ;
c) \(1\frac{3}{7}:1,24\) ; d) \(\frac{2\tfrac{1}{5}}{3\tfrac{1}{7}}\).
Tỉ số của hai số a và b có thể viết là \(\frac{a}{b}\). Cách viết này có khác gì cách viết phân số \(\frac{a}{b}\) không ? Cho ví dụ.
Chuột nặng hơn voi !
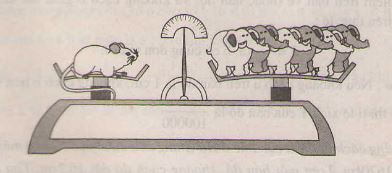
Một con chuột nặng 30g còn một con voi nặng 5 tấn. Tỉ số giữa khối lượng của một con chuột và khối lượng của một con voi là \(\frac{30}{5}=6\) , nghĩa là một con chuột nặng bằng 6 con voi ! Em có tin như vậy không ? Sai lầm ở chỗ nào ?
Tỉ số của hai số a và b bằng \(1\frac{1}{2}\). Tìm hai số đó biết a - b = 8
Khi nói đến vàng ba số 9 (999) ta hiểu rằng: Trong 1000g “vàng” này chứa tới 999g vàng nguyên chất , nghĩa là tỉ lệ vàng nguyên chất là \({{999} \over {1000}} = 99,9\%\)
Em hiểu thế nào khi nói đến vàng bốn số 9 (9999)?
Trong 40 kg nước biển có 2 kg muối. Tính tỉ số phần trăm muối trong nước biển.
Biết tỉ số phần trăm nước trong dưa chuột là 97,2%. Tính lượng nước trong 4 kg dưa chuột.
Tìm tỉ lệ xích của một bản đồ, biết rằng quãng đường từ Hà Nội đến Thái Nguyên trên bản đồ là 4 cm còn trong thực tế là 80 km.
Trên một bản vẽ kĩ thuật có tỉ lệ xích 1:125, chiều dài của một chiếc máy bay Bô – inh (Boeing) 747 là 56,408 cm. Tính chiều dài thật của chiếc máy bay đó.
Cầu Mỹ Thuận (h.12) nối hai đỉnh Tiền Giang và Vĩnh Long được khánh thành ngày 21-5-2000.

Cầu Mỹ Thuận là cây cầu treo hiện đại (cầu dây văng) đầu tiền ở nước ta với chiều dài 1535 m bắc ngang sông Tiền, một trong những con sôn rộng nhất Việt Nam. Nếu vẽ trên bản đồ tỉ lệ xích 1 : 20000 thì cây cầu này dài bao nhiêu xentimet?
Sử dụng máy tính bỏ túi
Dùng máy tính bỏ túi để tính tỉ số phần trăm của:
a) 65 và 160
b) 0,453195 và 0,15;
c) 1762384 và 4405960.
Với số liệu nêu trong  , hãy dựng biểu đồ phần trăm dưới dạng ô vuông.
, hãy dựng biểu đồ phần trăm dưới dạng ô vuông.
Điểm kiểm tra của lớp 6C đều trên trung bình và được biểu diễn như hình 16.
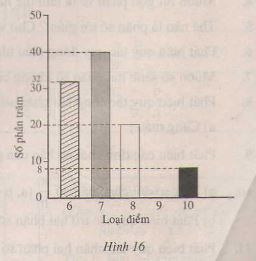
a) Có bao nhiêu phần trăm bài đạt điểm 10 ?
b) Loại điểm nào cao nhất ? Chiếm bao nhiêu phần trăm ?
c) Tỉ lệ bài đạt điểm 9 là bao nhiêu phần trăm ?
d) Tính tổng số bài kiểm tra toán của lớp 6C biết rằng có 16 bài đạt điểm 6.
Muốn đổ bê tông, người ta trộn 1 tạ xi măng, 2 tạ cát và 6 tạ sỏi.
a) Tính tỉ số phần trăm từng thành phần của bê tông.
b) Dựng biểu đồ ô vuông biểu diễn các tỉ số phần trăm đó.
Năm học 1998 – 1999, cả nước ta có 13076 trường tiểu học, 8583 trường THCS và 1641 trường THPT. Dựng biểu đồ cột biểu diễn tỉ số phần trăm các loại trường nói trên trong hệ thống Giáo dục phổ thông của Việt Nam.
Hãy biểu diễn bằng phần tô màu:
a) \(\frac{1}{4}\) của hình vuông
b) \(\frac{2}{3}\) của hình chữ nhật
Phần tô màu trong các hình vẽ sau biểu diễn các phân số nào?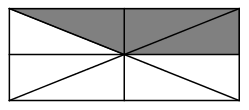
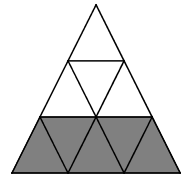
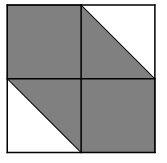
Viết các phân số sau:
a) Ba phần năm
b) Âm hai phần bảy
c) Mười hai phần mười bảy
d) Mười một phần năm
Viết các phép chia sau dưới dạng phân số:
a) (-3) : 5
b) (-2) : (-7)
c) 2 : (-11)
d) x chia cho 5 (x ∈ Z)
Dùng cả hai số x và y để viết thành phân số, mỗi số chỉ được viết một lần (x, y ∈ Z, x , y ≠ 0 )
Biểu diễn các số sau đây dưới dạng phân số với đơn vị là:
Mét: 23 cm, 47 mm
Mét vuông: 7dm2, 101 cm2
Viết tập hợp A các số nguyên x , biết rằng \(\frac{{ - 28}}{4} \le x < \frac{{ - 21}}{7}\)
Cho biểu thức \(B = \frac{4}{{n - 3}}\) với n là số nguyên
a) Số nguyên n phải có điều kiện gì để B là phân số?
b) Tìm phân số B, biết n = 0; n = 10 ; n = -2
Trong các cách viết sau cách nào cho ta phân số:
\(\begin{array}{l}
\left( A \right) - \frac{{3,15}}{6}\\
\left( B \right) - \frac{{1,5}}{{2,17}}\\
\left( C \right) - \frac{5}{6}\\
\left( D \right)\frac{3}{{ - 4}}
\end{array}\)
Số nguyên x thỏa mãn điều kiện \( - \frac{{42}}{7} < x < - \frac{{24}}{6}\) là
(A) -5
(B) -4;
(C) -6;
(D) -200
Hãy chọn đáp án đúng.
Cho phân số \(A = \frac{6}{{n - 3}}\) với n là số tự nhiên. Phân số A bằng bao nhiêu nếu n = 14; n = 5; n = 3.
Cho tập hợp M = {2; 3; 4}. Viết tập hợp P các số có tử và mẫu thuộc M, trong đó tử khác mẫu.
Tìm các cặp số tự nhiên n sao cho các phân số sau có giá trị là số nguyên:
a) \(\frac{{n + 4}}{n}\)
b) \(\frac{{n - 2}}{4}\)
c) \(\frac{{6}}{n-1}\)
d) \(\frac{{n}}{n-2}\)
Cho A = {−3; 0; 7}. Hãy viết tất cả các phân số \(\frac{a}{b}\) với a, b ∈ A
Tìm các số nguyên x, y biết:
a) \(\frac{x}{5} = \frac{6}{{ - 10}}\)
b) \(\frac{3}{y} = \frac{{ - 33}}{{77}}\)
Điền số thích hợp vào ô trống:
\(\begin{array}{l}
a)\frac{3}{4} = \frac{{...}}{{20}}\\
b)\frac{4}{5} = \frac{{12}}{{...}}\\
c)\frac{{...}}{9} = \frac{{ - 16}}{{36}}\\
d)\frac{7}{{...}} = \frac{{21}}{{ - 39}}
\end{array}\)
Viết các phân số sau dưới dạng phân số có mẫu dương:
\(\frac{{ - 52}}{{ - 71}};\frac{4}{{ - 17}};\frac{5}{{ - 29}};\frac{{31}}{{ - 33}}\)
Lập các cặp phân số bằng nhau từ đẳng thức: 2 x 36 = 8 x 9
Lập các cặp phân số bằng nhau từ đẳng thức: (-2).(-14) = 4.7
Tìm các cặp số nguyên x, y biết:
a) \(\frac{x}{3} = \frac{4}{y}\)
b) \(\frac{x}{y} = \frac{2}{7}\)
Tìm các cặp số nguyên x, y, z biết:
\(\frac{{ - 4}}{8} = \frac{x}{{ - 10}} = \frac{{ - 7}}{y} = \frac{z}{{ - 24}}\)
Lập các cặp phân số bằng nhau từ bốn trong năm số sau: 2; 4; 8; 16; 32
Phân số bằng phân số \(\frac{{ - 16}}{{24}}\) là :
\(\begin{array}{l}
\left( A \right)\frac{{16}}{{24}}\\
\left( B \right)\frac{{ - 2}}{{ - 3}}\\
\left( C \right)\frac{{ - 2}}{3}\\
\left( D \right)\frac{{ - 16}}{{ - 24}}
\end{array}\)
Các cặp phân số bằng nhau là:
(A) \(\frac{{ - 3}}{4}\) và \(\frac{{ - 4}}{3}\)
(B) \( - \frac{2}{3}\) và \(\frac{{6}}{9}\)
(C) \(\frac{{3}}{7}\) và \(\frac{{ - 3}}{7}\)
(D) \(\frac{{7}}{8}\) và \(\frac{{ - 35}}{{ - 40}}\)
Hãy chọn câu trả lời đúng.
Tìm các số nguyên x và y, biết :
\(\frac{{ - 2}}{x} = \frac{y}{3}\) và x < 0 < y
Tìm các số nguyên x và y, biết:
\(\frac{{x - 3}}{{y - 2}} = \frac{3}{2}\) và x - y = 4
Điền số thích hợp vào ô trống:
\(\frac{{...}}{{ - 2}} = \frac{{...}}{3} = \frac{{...}}{{ - 5}} = \frac{7}{{...}} = \frac{{ - 9}}{{...}} = 1\)
Điền số thích hợp vào ô trống:
Khi nào thì một phân số có thể viết dưới dạng một số nguyên
Một vòi nước chảy 3 giờ thì đầy bể. Hỏi khi chảy cùng 1 giờ; 59 phút; 127 phút thì lượng nước đã chảy chiếm bao nhiêu phần bể?
Trên hành tinh của chúng ta đại dương nào lớn nhất?
Em hãy điền các số thích hợp vào ô trống để có các đẳng thức đúng. Sau đó, viết các chữ số tương ứng với các chữ số tìm được vào các ô ở hàng dưới cùng, em sẽ trả lời được câu hỏi nêu trên.
Cho biểu thức: \(A = \frac{3}{{n - 2}}\)
Tìm các số nguyên n để biểu thức A là phân số
Tìm các số nguyên n để biểu thức A là một số nguyên
Giải thích tại sao các phân số sau đây bằng nhau:
a) \(\frac{{ - 21}}{{28}} = \frac{{ - 39}}{{52}}\)
b) \(\frac{{ - 1717}}{{2323}} = \frac{{ - 171717}}{{232323}}\)
Có thể có phân số \(\frac{a}{b}\) (a, b ∈ Z, b ≠ 0) sao cho:
\(\frac{a}{b} = \frac{{a.m}}{{b.n}}\) (m, n ∈ Z, m , n ≠ 0 , m ≠ n) hay không?
Phân số có mẫu dương và không bằng phân số \(\frac{{ - 3}}{7}\) là:
(A) \(\frac{{ - 6}}{14}\)
(B) \(\frac{{ - 15}}{25}\)
(C) \(\frac{{ - 24}}{63}\)
(D) \(\frac{{ - 12}}{28}\)
Hãy chọn đáp số đúng.
Phân số có tử là 2, lớn hơn \(\frac{1}{9}\) và nhỏ hơn \(\frac{1}{8}\) là:
(A) \(\frac{2}{9}\)
(B) \(\frac{2}{8}\)
(C) \(\frac{2}{17}\)
(D) \(\frac{2}{10}\)
Hãy chọn đáp án đúng
Cho ba phân số \(\frac{1}{{ - 2}};\frac{5}{{ - 3}};\frac{3}{{ - 4}}\)
a) Viết ba phân số theo thứ tự bằng các phân số trên và có mẫu là những số dương.
b) Viết ba phân số theo thứ tự bằng các phân số trên và có mẫu là những số dương giống nhau.
Dùng tính chất cơ bản của phân số hãy giải thích vì sao các phân số sau đây bằng nhau :
a) \(\frac{{36}}{{84}} = \frac{{42}}{{98}}\)
b) \(\frac{{123}}{{237}} = \frac{{123123}}{{237237}}\)
Rút gọn các phân số sau thành phân số tối giản
a) \(\frac{{ - 270}}{{450}}\)
b) \(\frac{{11}}{{-143}}\)
c) \(\frac{{32}}{{12}}\)
d) \(\frac{{ - 26}}{{-156}}\)
Một tủ sách có 1400 cuốn, trong số đó có 600 cuốn sách toán học, 360 cuốn sách văn học, 108 cuốn sách ngoại ngữ, 35 cuốn sách tin học, còn lại là truyện tranh. Hỏi mỗi loại sách trên chiếm bao nhiêu phần của tổng số sách?
Rút gọn:
\(\begin{array}{l}
a)\frac{{4.7}}{{9.32}}\\
b)\frac{{3.21}}{{14.15}}\\
c)\frac{{2.5.13}}{{26.35}}\\
d)\frac{{9.6 - 9.3}}{{18}}\\
e)\frac{{17.5 - 17}}{{3 - 20}}\\
f)\frac{{49 + 7.49}}{{49}}
\end{array}\)
Viết các số đo thời gian sau đây với đơn vị là giờ (chú ý rút gọn nếu có thể):
a) 30 phút
b) 25 phút
c) 100 phút
Đổi ra mét vuông (viết dưới dạng phân số tối giản):
a) 45 dm2
b) 300 cm2
c) 57500 mm2
Bạn Lan thường ngủ 9 giờ mỗi ngày. Hỏi thời gian bạn Lan thức chiếm bao nhiêu phần của ngày?
Một bể nước có dung tích 5000 lít. Người ta đã bơm 3500 lít nước vào bề. Hỏi lượng nước cần bơm tiếp cho đầy bể bằng mấy phần dung dịch của bể?
Tìm các cặp phân số bằng nhau trong các phân số sau đây:
\(\frac{8}{{18}};\frac{{ - 35}}{{14}};\frac{{88}}{{56}};\frac{{ - 12}}{{ - 27}};\frac{{11}}{7};\frac{{ - 5}}{2}\)
Trong các phân số sau đây, tìm phân số không bằng các phân số còn lại:
\(\frac{{15}}{{35}};\frac{{ - 6}}{{33}};\frac{{21}}{{49}};\frac{{ - 21}}{{91}};\frac{{14}}{{ - 77}};\frac{{ - 24}}{{104}};\frac{6}{{22}}\)
Tìm tất cả các phân số bằng phân số \(\frac{{21}}{{28}}\) và có mẫu là số tự nhiên nhỏ hơn 19
Tìm các số nguyên x sao cho: \(\frac{2}{x} = \frac{x}{8}\)
Rút gọn
a) \(A = \frac{{4116 - 14}}{{10290 - 35}}\)
b) \(B = \frac{{2929 - 101}}{{2.1919 + 404}}\)
Bạn Minh đã tìm ra một cách "rút gọn" phân số rất đơn giản. Này nhé:
\(\begin{array}{l}
\frac{{16}}{{64}} = \frac{{1\not 6}}{{\not 64}} = \frac{1}{4}\\
\frac{{26}}{{65}} = \frac{{2\not 6}}{{\not 65}} = \frac{2}{5}
\end{array}\)
("Rút gọn" cho 6)
\(\begin{array}{l}
\frac{{19}}{{95}} = \frac{{1\not 9}}{{\not 95}} = \frac{1}{5}\\
\frac{{49}}{{98}} = \frac{{4\not 9}}{{\not 98}} = \frac{4}{8} = \frac{1}{2}
\end{array}\)
("Rút gọn" cho 9)
Em hãy kiểm tra xem các kết quả tìm được có đúng không?
Em có thể áp dụng "phương pháp" này để rút gọn các phân số có dạng \(\frac{{ab}}{{bc}}\) hay không?
Bạn Việt đã tìm ra một vài phân số có tính chất đặc biệt sau đây: chẳng hạn phân số \(\frac{{12}}{{36}}\) . Nếu đổi chỗ các chữ số ở tử cũng như ở mẫu thì ta được phân số \(\frac{{21}}{{63}}\) và ta có \(\frac{{12}}{{36}}\) = \(\frac{{21}}{{63}}\). Phân số \(\frac{{12}}{{26}}\) cũng có tính chất tương tự. Em thử kiểm tra xem. Em có tìm được hai phân số khác cũng có tính chất tương tự này không?
Chứng tỏ rằng \(\frac{{12n + 1}}{{30n + 2}}\) là phân số tối giản (n ∈ N)
Cộng cả tử và mẫu của phân số \(\frac{{23}}{{40}}\) với cùng một số tự nhiên n rồi rút gọn, ta được phân số \(\frac{{3}}{{4}}\). Tìm số n
Phân số nào dưới đây là phân số tối giản?
\(\begin{array}{l}
\left( A \right)\frac{{125}}{{300}}\\
\left( B \right)\frac{{416}}{{634}}\\
\left( C \right)\frac{{351}}{{417}}\\
\left( D \right)\frac{{141}}{{143}}
\end{array}\)
Hãy chọn đáp án đúng.
Phân số nào dưới đây không là phân số tối giản?
\(\begin{array}{l}
\left( A \right)\frac{8}{{81}}\\
\left( B \right)\frac{{28}}{{91}}\\
\left( C \right)\frac{{176}}{{177}}\\
\left( D \right)\frac{{17}}{{35}}
\end{array}\)
Hãy chọn đáp án đúng.
Viết tập hợp A các phân số bằng phân số \(\frac{{ - 21}}{{35}}\)
Viết tập hợp B các phân số bằng \(\frac{{15}}{{48}}\) mà tử và mẫu là các số tự nhiên có hai chữ số.
Cho phân số \(A = \frac{{n + 1}}{{n - 3}}\), \(\left( {n \in Z,n \ne 3} \right)\)
Tìm n để A là phân số tối giản.
Tìm mẫu chung nhỏ nhất của các phân số sau:
a) \(\frac{1}{5}\) và \(\frac{-2}{7}\)
b) \(\frac{2}{5}\); \(\frac{3}{25}\) và \(\frac{-1}{3}\)
c) \(\frac{5}{12}\), \(\frac{-3}{8}\), \(\frac{-2}{3}\) và \(\frac{7}{24}\)
Viết các phân số sau dưới dạng phân số có mẫu là 36:
\(\frac{{ - 1}}{3};\frac{2}{3};\frac{{ - 1}}{{ - 2}};\frac{6}{{ - 24}};\frac{{ - 3}}{4};\frac{{10}}{{60}};\frac{{ - 5}}{6}\)
Viết các số sau dưới dạng phân số có mẫu là 12
1; -5; \(\frac{{ - 3}}{4}\); 0
Rút gọn rồi quy đồng mẫu các phân số sau:
\(\frac{{3.4 + 3.7}}{{6.5 + 9}}\) và \(\frac{{6.9 - 2.17}}{{63.3 - 119}}\)
So sánh các phân số sau rồi nêu nhận xét
a) \(\frac{{12}}{{23}}\) và \(\frac{{1212}}{{2323}}\)
b) \(\frac{{-3434}}{{4141}}\) và \(\frac{{-34}}{{41}}\)
Quy đồng mẫu các phân số:
a) \(\frac{{17}}{{320}}\) và \(\frac{{-9}}{{80}}\)
b) \(\frac{{-7}}{{10}}\) và \(\frac{{1}}{{33}}\)
c) \(\frac{{-5}}{{14}}\); \(\frac{{3}}{{20}}\) và \(\frac{{9}}{{70}}\)
d) \(\frac{{10}}{{42}}\); \(\frac{{-3}}{{28}}\) và \(\frac{{-55}}{{132}}\)
Khi so sánh hai phân số \(\frac{3}{7}\) và \(\frac{2}{5}\) , hai bạn Liên và Oanh đều đi đến kết quả \(\frac{3}{7}\) lớn hơn \(\frac{2}{5}\) nhưng mỗi người giải thích một khác. Liên cho rằng : "Khi quy đồng mẫu thì \(\frac{3}{7}\) = \(\frac{15}{35}\) và \(\frac{2}{5}\) = \(\frac{14}{35}\) mà \(\frac{15}{35}\) lớn hơn \(\frac{14}{35}\) nên \(\frac{3}{7}\) lớn hơn \(\frac{2}{5}\) . Còn Oanh lại giải thích: "Sở dĩ \(\frac{3}{7}\) lớn hơn \(\frac{2}{5}\) vì 3 lớn hơn 2 và 7 lớn hơn 5"". Theo em , bạn nào giải thích đúng ? Vì sao?
Tìm phân số có mẫu số bằng 7, biết rằng khi cộng tử với 16 , nhân mẫu với 5 thì giá trị của phân số đó không thay đổi.
Cho các phân số \(\frac{{13}}{{28}}\) và \(\frac{{21}}{{50}}\). Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Mẫu chung của hai phân số đã cho là 100;
b) Mẫu chung của hai phân số đã cho là 700;
c) Mẫu chung của hai phân số đã cho là 140;
d) Mẫu chung của hai phân số đã cho là 1400.
Trong các khẳng định sau, khẳng định nào đúng?
a) Các phân số \(\frac{3}{5}\) và \(\frac{6}{7}\) có thể quy đồng mẫu thành \(\frac{6}{10}\) và \(\frac{6}{7}\)
b) Các phân số \(\frac{1}{3},\frac{5}{6},\frac{2}{5}\) có thể quy đồng mẫu thành \(\frac{{10}}{{30}},\frac{{25}}{{30}},\frac{{12}}{{30}}\)
c) Các phân số \(\frac{2}{{25}},\frac{7}{{15}},\frac{{11}}{6}\) có thể quy đồng mẫu thành \(\frac{{18}}{{150}},\frac{{70}}{{150}},\frac{{255}}{{150}}\)
Rút gọn rồi quy đồng mẫu các phân số sau:
\(\begin{array}{l}
A = \frac{{3469 - 54}}{{6938 - 108}}\\
B = \frac{{2468 - 98}}{{3702 - 147}}
\end{array}\)
Rút gọn rồi quy đồng mẫu các phân số sau:
\(\begin{array}{l}
C = \frac{{1010}}{{1008.8 - 994}}\\
D = \frac{{1.2.3 + 2.4.6 + 3.6.9 + 5.10.15}}{{1.3.6 + 2.6.12 + 3.9.18 + 5.15.30}}
\end{array}\)
Tìm số nguyên x, biết rằng \(\frac{{2x - 9}}{{240}} = \frac{{39}}{{80}}\)
Điền số thích hợp vào chỗ trống:
\(\begin{array}{l}
a)\frac{{ - 12}}{{17}} < \frac{{...}}{{17}} < \frac{{...}}{{17}} < \frac{{...}}{{17}} < \frac{{ - 8}}{{17}}\\
b)\frac{{ - 1}}{2} < \frac{{...}}{{24}} < \frac{{...}}{{12}} < \frac{{...}}{8} < \frac{{ - 1}}{3}
\end{array}\)
a) Thời gian nào dài hơn: \(\frac{1}{2}\) giờ hay \(\frac{4}{5}\)?
b) Đoạn thẳng nào ngắn hơn: \(\frac{2}{3}\) mét hay \(\frac{3}{5}\) mét ?
c) Khối lượng nào lớn hơn: \(\frac{6}{7}\) kilogam hay \(\frac{7}{8}\) kilogam?
So sánh các phân số:
a) \(\frac{5}{{24}};\frac{{5 + 10}}{{24}};\frac{5}{8}\)
b) \(\frac{4}{9};\frac{{6 + 9}}{{6.9}};\frac{2}{3}\)
So sánh các phân số:
a) \(\frac{{14}}{{21}}\) và \(\frac{{60}}{{72}}\)
b) \(\frac{{38}}{{133}}\) và \(\frac{{129}}{{344}}\)
So sánh các phân số:
a) \(\frac{{17}}{{200}}\) và \(\frac{{17}}{{314}}\)
b) \(\frac{{11}}{{54}}\) và \(\frac{{22}}{{37}}\)
c) \(\frac{{141}}{{893}}\) và \(\frac{{159}}{{901}}\)
Cho hình vuông gồm 9 ô . Hãy sắp xếp các phân số sau đây vào các ô trống sao cho trong mỗi hàng các phân số tăng dần từ trái sang phải và trong mỗi cột, các phân số tăng dần từ trên xuống dưới:
\(\frac{9}{{19}}\); \(\frac{-25}{{19}}\); \(\frac{20}{{19}}\); \(\frac{42}{{19}}\); \(\frac{30}{{19}}\); \(\frac{14}{{19}}\); \(\frac{-13}{{19}}\)
.jpg)
Cũng như yêu cầu ở bào 54 với các phân số:
\(\frac{1}{3};\frac{1}{5};\frac{{ - 2}}{{15}};\frac{1}{6};\frac{{ - 2}}{{ - 5}};\frac{{ - 1}}{{10}};\frac{4}{{15}}\)
.jpg)
Cho hai phân số \(\frac{{ - 3}}{8}\) và \(\frac{{ - 2}}{5}\). Chỉ cần so sánh hai tích (-3).5 và 8.(-2) cũng có thể kết luận được rằng \(\frac{{ - 3}}{8}\) > \(\frac{{ - 2}}{5}\). Em có thể giải thích được không ? hãy phát biểu và chứng minh cho trường hợp tổng quát khi so sánh hai phân số \(\frac{{a}}{b}\) và \(\frac{{c}}{d}\) (a, b, c, d ∈ Z ; b > 0 ; d > 0)
Điền số thích hợp vào ô trống
\(\frac{{ - 8}}{{15}} < \frac{{...}}{{40}} < \frac{{ - 7}}{{15}}\)
Trong các phân số sau, phân số lớn hơn \(\frac{3}{5}\) là:
(A) \(\frac{11}{20}\)
(B) \(\frac{8}{15}\)
(C) \(\frac{22}{35}\)
(D) \(\frac{23}{40}\)
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Không có phân số nào lớn hơn \(\frac{3}{7}\) và nhỏ hơn \(\frac{4}{7}\)
b) Nếu một phân số có tử lớn hơn mẫu thì phân số đó lớn hơn 1
Tìm hai phân số có mẫu khác nhau, các phân số này lớn hơn \(\frac{1}{5}\) nhưng nhỏ hơn \(\frac{1}{4}\) .
a) Chứng tỏ rằng trong hai phân số cùng tử, tử và mẫu đều dương, phân số nào có mẫu nhỏ hơn thì lớn hơn.
Nếu a, b, c > 0 và b < c thì \(\frac{a}{b} > \frac{a}{c}\)
b) Áp dụng tính chất trên, hãy so sánh các phân số sau:
\(\frac{9}{{37}}\) và \(\frac{12}{{49}}\); \(\frac{30}{{235}}\) và \(\frac{168}{{1323}}\); \(\frac{321}{{454}}\) và \(\frac{325}{{451}}\)
a) Cho phân số \(\frac{a}{b}\) (a, b ∈ N, \(b \ne 0\))
Giả sử \(\frac{a}{b}\) < 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
\(\frac{a}{b}\) < \(\frac{a+m}{b+m}\)
b) Áp dụng kết quả ở câu a) để so sánh \(\frac{434}{561}\) và \(\frac{441}{568}\)
a) Cho phân số \(\frac{a}{b}\) (a, b ∈ N, b ≠ 0)
Giả sử \(\frac{a}{b}\) > 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
\(\frac{a}{b}\) > \(\frac{a+m}{b+m}\)
b) Áp dụng kết quả ở câu a) để so sánh \(\frac{{247}}{{142}}\) và \(\frac{{246}}{{151}}\)
So sánh: \(A = \frac{{{{17}^{18}} + 1}}{{{{17}^{19}} + 1}}\) và \(B = \frac{{{{17}^{17}} + 1}}{{{{17}^{18}} + 1}}\)
So sánh \(C = \frac{{{{98}^{99}} + 1}}{{{{98}^{89}} + 1}}\) và \(D = \frac{{{{98}^{98}} + 1}}{{{{98}^{88}} + 1}}\)
Cộng các phân số sau
a) \(\frac{1}{6} + \frac{2}{5}\)
b) \(\frac{3}{5} + \frac{{ - 7}}{4}\)
c) \(\left( { - 2} \right) + \frac{{ - 5}}{8}\)
Cộng các phân số (rồi rút gọn kết quả nếu có thể):
a) \(\frac{1}{{ - 8}} + \frac{{ - 5}}{8}\)
b) \(\frac{4}{{13}} + \frac{{ - 12}}{{39}}\)
c) \(\frac{{ - 1}}{{21}} + \frac{{ - 1}}{{28}}\)
Tính các tổng dưới đây sau khi đã rút gọn phân số
a) \(\frac{{ - 3}}{{29}} + \frac{{16}}{{58}}\)
b) \(\frac{8}{{40}} + \frac{{ - 36}}{{45}}\)
c) \(\frac{{ - 8}}{{18}} + \frac{{ - 15}}{{27}}\)
Tìm x biết:
a) \(x = \frac{1}{4} + \frac{2}{{13}}\)
b) \(\frac{x}{3} = \frac{2}{3} + \frac{{ - 1}}{7}\)
Hoàn thành các bảng sau
Hai người cùng làm một công việc. Nếu làm riêng, người thứ nhất phải mất 4 giờ, người thứ hai mất 3 giờ. Hỏi nếu làm chung thì mỗi giờ cả hai người làm được mấy phần công việc?
Tìm tổng các phân số lớn hơn \(\frac{{ - 1}}{7}\), nhỏ hơn \(\frac{{ - 1}}{8}\) và có tử là -3.
Viết phân số \(\frac{7}{{25}}\) dưới dạng tổng hai phân số tối giản có mẫu là 25 và tử là số nguyên khác 0 có một chữ số
Tổng của hai phân số \(\frac{7}{{15}}\) và \(\frac{-2}{{5}}\) bằng:
(A) \(\frac{5}{{10}}\)
(B) \(\frac{5}{{20}}\)
(C) \(\frac{1}{{15}}\)
(D) \(\frac{-1}{{15}}\)
Hãy chọn đáp án đúng
Tổng của ba phân số \(\frac{1}{3}\); \(\frac{4}{7}\) và \(\frac{-5}{21}\) bằng
(A) \(\frac{2}{3}\)
(B) \(\frac{3}{31}\)
(C) \(\frac{24}{21}\)
(D) \(\frac{27}{42}\)
Không tính tổng của ba phân số sau, hãy chứng tỏ rằng tổng đó nhỏ hơn 2
\(A = \frac{{11}}{{29}} + \frac{9}{{17}} + \frac{{10}}{{19}}\)
Cho \(A = \frac{{2011}}{{2012}} + \frac{{2012}}{{2013}}\) và \(B = \frac{{2011 + 2012}}{{2012 + 2013}}\)
Trong hai số A và B, số nào lớn hơn?
Viết phân số \(\frac{7}{{16}}\) và thành tổng của hai phân số tối giản có mẫu khác nhau.
Tính nhanh
\(\frac{1}{2} + \frac{{ - 1}}{3} + \frac{1}{4} + \frac{{ - 1}}{5} + \frac{1}{6} + \frac{{ - 1}}{7} + \frac{1}{8} + \frac{1}{7} + \frac{{ - 1}}{6} + \frac{1}{5} + \frac{{ - 1}}{4} + \frac{1}{3} + \frac{{ - 1}}{2}\)
Cắt một tấm bìa hình tròn bán kính 2,5 cm thành bốn phần không bằng nhau như hình vẽ. Em hãy đặt các miếng bìa đã cắt cạnh nhau để có được:
a) \(\frac{1}{2}\) hình tròn
b) \(\frac{2}{3}\) hình tròn
c) \(\frac{2}{9}\); \(\frac{5}{6}\); \(\frac{5}{9}\) hình tròn
d) \(\frac{7}{18}\); \(\frac{17}{18}\); \(\frac{18}{18}\) hình tròn
a) Điền số thích hợp vào ô trống
\(\frac{{ - 8}}{3} + \frac{{ - 1}}{3} < .... < \frac{{ - 2}}{7} + \frac{{ - 5}}{7}\)
b) Tìm tập hợp các số x ∈ Z, biết rằng:
\(\frac{{ - 5}}{6} + \frac{8}{3} + \frac{{29}}{{ - 6}} \le x \le \frac{{ - 1}}{2} + 2 + \frac{5}{2}\)
Vòi nước A chảy vào một bể không có nước trong 4 giờ thì đầy. Vòi nước B chảy đầy bể ấy trong 5 giờ. Hỏi:
a) Trong 1 giờ, mỗi vòi chảy được lượng nước bằng mấy phần bể?
b) Trong 1 giờ, cả hai vòi chảy được lượng nước bằng mấy phần bể?
Ba người cùng làm một công việc. Nếu làm riêng, người thứ nhất phải mất 4 giờ, người thứ hai 3 giờ, người thứ ba 6 giờ. Hỏi nếu làm chung thì mỗi giờ cả ba người làm được mấy phần công việc?
Tính nhanh
\(\begin{array}{l}
A = \frac{5}{{13}} + \frac{{ - 5}}{7} + \frac{{ - 20}}{{41}} + \frac{8}{{13}} + \frac{{ - 21}}{{41}}\\
B = \frac{{ - 5}}{9} + \frac{8}{{15}} + \frac{{ - 2}}{{11}} + \frac{4}{{ - 9}} + \frac{7}{{15}}
\end{array}\)
Phân số \(\frac{{ - 8}}{{15}}\) có thể viết được dưới dạng tổng của ba phân số có tử bằng -1 và mẫu khác nhau
Chẳng hạn:
\(\begin{array}{l}
\frac{{ - 8}}{{15}} = \frac{{ - 16}}{{30}} = \frac{{\left( { - 10} \right) + \left( { - 5} \right) + \left( { - 1} \right)}}{{30}}\\
= \frac{{ - 1}}{3} + \frac{{ - 1}}{6} + \frac{{ - 1}}{{30}}
\end{array}\)
Em có thể tìm được một cách viết khác hay không?
Cho \(S = \frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + \frac{1}{{14}} + \frac{1}{{15}} + \frac{1}{{16}} + \frac{1}{{17}} + \frac{1}{{18}} + \frac{1}{{19}} + \frac{1}{{20}}\)
Hãy so sánh S và \(\frac{1}{2}\)
Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được kết quả đúng:
\(\begin{array}{l}
\left( A \right)\frac{{ - 2}}{5} + \frac{3}{{ - 4}} + \frac{6}{7} + \frac{3}{4} + \frac{2}{5}\\
\left( B \right)\frac{{ - 1}}{8} + \frac{7}{9} + \frac{{ - 7}}{8} + \frac{6}{7} + \frac{2}{{14}}\\
\left( C \right)\frac{5}{{11}} + \frac{{16}}{{22}} + \frac{{ - 12}}{4} + \frac{{ - 2}}{{11}}\\
\left( D \right)\frac{7}{{23}} + \frac{{ - 10}}{{18}} + \frac{{ - 4}}{9} + \frac{{16}}{{23}}
\end{array}\)
\(\begin{array}{l}
1) - 2\\
2)0\\
3)\frac{6}{7}\\
4)3\\
5)\frac{7}{9}
\end{array}\)
Viết \(\frac{3}{4}\) thành tổng của ba phân số tối giản, có mẫu chung là 16, tử là các số tự nhiên khác 0, được kết quả là
\(\begin{array}{l}
\left( A \right)\frac{1}{2} + \frac{3}{{16}} + \frac{1}{{16}}\\
\left( B \right)\frac{1}{4} + \frac{1}{8} + \frac{3}{{16}}\\
\left( C \right)\frac{1}{4} + \frac{5}{8} + \frac{1}{{16}}\\
\left( D \right)\frac{1}{4} + \frac{1}{8} + \frac{5}{{16}}
\end{array}\)
Hãy chọn đáp án đúng
Chứng tỏ rằng tổng của các phân số sau đây lớn hơn \(\frac{1}{2}\)
\(S = \frac{1}{{50}} + \frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{98}} + \frac{1}{{99}}\)
Cho tổng \(A = \frac{1}{{10}} + \frac{1}{{11}} + \frac{1}{{12}} + ... + \frac{1}{{99}} + \frac{1}{{100}}\)
Chứng tỏ rằng A > 1
Vòi nước A chảy đầy một bể không có nước mất 3 giờ, vòi nước B chảy đầy bể đó mất 4 giờ. Hỏi trong 1 giờ, vòi nào chảy được nhiều nước hơn và nhiều hơn bao nhiêu?
Điền phân số thích hợp vào ô trống:
\(\begin{array}{l}
a)\frac{3}{7} + ... = \frac{{ - 2}}{7}\\
b)... + \frac{{ - 5}}{{11}} = \frac{{ - 13}}{{11}}\\
c)\frac{6}{{18}} + \frac{3}{{18}} = ...\\
d)\frac{{ - 6}}{{17}} + ... = \frac{{ - 6}}{{17}}
\end{array}\)
Thời gian 1 ngày của Cường được phân phối như sau:
- Ngủ: \(\frac{1}{3}\) ngày;
- Học ở trường: \(\frac{1}{6}\) ngày
- Chơi thể thao: \(\frac{1}{12}\) ngày
- Học và làm bài tập ở nhà: \(\frac{1}{8}\) ngày
- Giúp đỡ gia đình việc vặt: \(\frac{1}{24}\) ngày
Hỏi Cường còn bao nhiêu thời gian rỗi?
Một khay đựng 4 quả chuối, 1 quả táo và 1 quả cam. Biết rằng quả táo nặng \(\frac{1}{8}\) kg, quả cam nặng \(\frac{1}{3}\) kg, quả chuối nặng \(\frac{1}{10}\) kg. Hỏi khay nặng bao nhiêu nếu khối lượng tổng cộng là \(\frac{5}{4}\) kg?
Điền phân số thích hợp vào ô trống
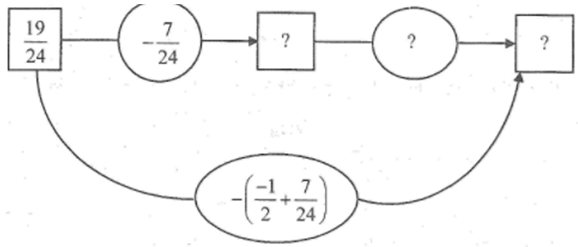
Hoàn thành sơ đồ sau:
Kiểm tra lại kết quả bằng cách thực hiện phép tính trong ngoặc trước:
\(\frac{{19}}{{24}} - \left( {\frac{{ - 1}}{2} + \frac{7}{{24}}} \right) = ...\)
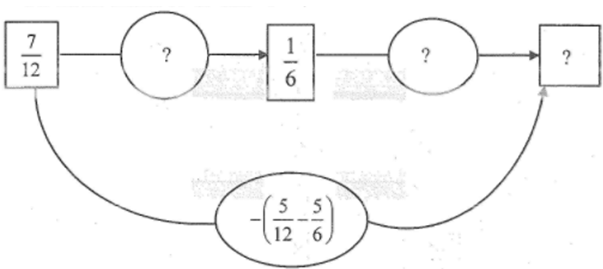
Hoàn thành sơ đồ sau:
Kiểm tra lại kết quả bằng cách thực hiện phép tính trong ngoặc trước:
\(\frac{7}{{12}} - \left( {\frac{5}{{12}} - \frac{5}{6}} \right) = ...\)
a) Tính: \(1 - \frac{1}{2};\frac{1}{2} - \frac{1}{3};\frac{1}{3} - \frac{1}{4};\frac{1}{4} - \frac{1}{5};\frac{1}{5} - \frac{1}{6}\)
b) Sử dụng kết quả của câu a) để tính nhanh tổng sau:
\(\frac{1}{2} + \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{20}} + \frac{1}{{30}}\)
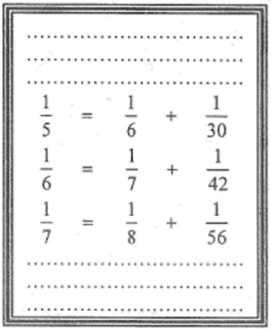
Một tài liệu "bí hiểm". Đây là mẩu giấy duy nhất còn sót lại của một tài liệu.
Em hãy khôi phục lại ba dòng trên và ba dòng tiếp theo của tài liệu theo quy luật các phép tính của ba dòng còn lại.
Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được kết quả đúng:
(A) Số đối của (-3)/4 là
(B) Số đối của (-7)/11 là
(C) Số đối của 7/3 là
(D) Số đối của 0 là
1) 7/11
2) 0
3) 3/7
4) 3/4
5) (-7)/3
Kết quả của phép tính \(\frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6}\) là:
\(\begin{array}{l}
\left( A \right)\frac{{17}}{{60}}\\
\left( B \right)\frac{{13}}{{60}}\\
\left( C \right)\frac{7}{{60}}\\
\left( D \right)\frac{{23}}{{60}}
\end{array}\)
a) Chứng tỏ rằng n ∈ N, n khác 0 thì: \(\frac{1}{{n\left( {n + 1} \right)}} = \frac{1}{n} - \frac{1}{{n + 1}}\)
b) Áp dụng kết quả ở câu a) để tính nhanh:
\(A = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{9.10}}\)
Tính nhanh
\(A = \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{20}} + \frac{1}{{30}} + \frac{1}{{42}} + \frac{1}{{56}}\)
Tính nhanh
\(B = \frac{1}{{15}} + \frac{1}{{35}} + \frac{1}{{63}} + \frac{1}{{99}} + \frac{1}{{143}}\)
Tính nhanh
\(C = \frac{1}{2} + \frac{1}{{14}} + \frac{1}{{35}} + \frac{1}{{65}} + \frac{1}{{104}} + \frac{1}{{152}}\)
Chứng tỏ rằng:
\(D = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{10}^2}}} < 1\)
Làm tính nhân:
a) \(\frac{{ - 1}}{3}.\frac{5}{7}\)
b) \(\frac{{ - 15}}{{16}}.\frac{8}{{ - 25}}\)
c) \(\frac{{ - 21}}{{24}}.\frac{8}{{ - 14}}\)
Tính
a) \(\frac{{ - 5}}{{13}}.26\)
b) \({\left( {\frac{{ - 2}}{7}} \right)^2}\)
c) \(\left( {2 - \frac{1}{2}} \right).\left( {\frac{{ - 3}}{4} + \frac{1}{2}} \right)\)
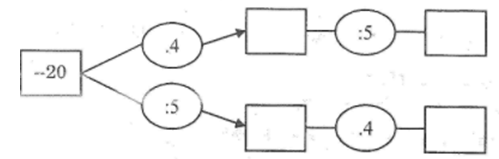
Hoàn thành sơ đồ sau để thực hiện phép nhân \( - 20.\frac{4}{5}\)
Từ cách làm trên , em hãy điền các từ thích hợp vào câu sau:
Khi nhân một số nguyên với một phân số, ta có thể:
- Nhân số đó với ….rồi lấy kết quả ….hoặc
- Chia số đó cho …rồi lấy kết quả ….
Áp dụng:
\(\begin{array}{l}
a)\left( { - 15} \right).\frac{3}{5}\\
b)42.\frac{{ - 6}}{7}\\
c)\left( { - 26} \right).\frac{3}{{ - 13}}\\
d)\left( { - 12} \right).\frac{2}{5}\\
e)\left( { - 17} \right).\frac{{ - 3}}{{52}}
\end{array}\)
Tính
\(\begin{array}{l}
a)\frac{2}{3} + \frac{1}{5}.\frac{{10}}{7}\\
b)\frac{7}{{12}} - \frac{{27}}{7}.\frac{1}{{18}}\\
c)\left( {\frac{{23}}{{41}} - \frac{{15}}{{82}}} \right).\frac{{41}}{{25}}\\
d)\left( {\frac{4}{5} + \frac{1}{2}} \right).\left( {\frac{3}{{13}} - \frac{8}{{13}}} \right)
\end{array}\)
a) Cho hai phân số \(\frac{1}{n}\) và \(\frac{1}{n+1}\) (n ∈ Z, n > 0) . Chứng tỏ rằng tích của phân số này bằng hiệu của chúng
b) Áp dụng kết quả trên để tính các giá trị của biểu thức sau:
\(\begin{array}{l}
A = \frac{1}{2}.\frac{1}{3} + \frac{1}{3}.\frac{1}{4} + \frac{1}{4}.\frac{1}{5} + \frac{1}{5}.\frac{1}{6} + \frac{1}{6}.\frac{1}{7} + \frac{1}{7}.\frac{1}{8} + \frac{1}{8}.\frac{1}{9}\\
B = \frac{1}{{30}} + \frac{1}{{42}} + \frac{1}{{56}} + \frac{1}{{72}} + \frac{1}{{90}} + \frac{1}{{110}} + \frac{1}{{132}}
\end{array}\)
Cho hai phân số \(\frac{a}{b}\) và \(\frac{a}{c}\) có b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0). Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng. Thử lại với a = 8; b = -3
\(\frac{5}{{38}}\) là tích của hai phân số nào:
\(\begin{array}{l}
\left( A \right)\frac{{ - 5}}{2}.\frac{1}{{ - 19}}\\
\left( B \right)\frac{{ - 5}}{{-19}}.\frac{1}{2}\\
\left( C \right)\frac{5}{{ - 2}}.\frac{{ - 1}}{{19}}\\
\left( D \right)\frac{1}{{ - 2}}.\frac{5}{{19}}
\end{array}\)
Tích \(\frac{1}{{11}}.\frac{1}{{12}}\) bằng
\(\begin{array}{l}
\left( A \right)\frac{1}{{12}} - \frac{1}{{11}}\\
\left( B \right)\frac{2}{{23}}\\
\left( C \right)\frac{1}{{11}} + \frac{1}{{12}}\\
\left( D \right)\frac{1}{{11}} - \frac{1}{{12}}
\end{array}\)
Hãy chọn đáp số đúng.
Tìm phân số tối giản \(\frac{a}{b}\) sao cho phân số \(\frac{a}{b-a}\) bằng 8 lần phân số \(\frac{a}{b}\).
Tìm số nguyên dương nhỏ nhất để khi nhân nó với mỗi một trong các phân số tối giản \(\frac{3}{4};\frac{{ - 5}}{{11}};\frac{7}{{12}}\) đều được tích là những số nguyên.
Điền các số thích hợp vào bảng sau:
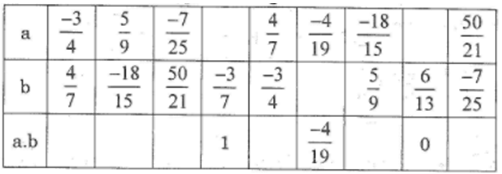
Tính nhanh các giá trị của biểu thức sau:
\(\begin{array}{l}
A = \frac{6}{7} + \frac{1}{7}.\frac{2}{7} + \frac{1}{7}.\frac{5}{7}\\
B = \frac{4}{9}.\frac{{13}}{3} - \frac{4}{3}.\frac{{40}}{9}
\end{array}\)
Áp dụng các tính chất của phép nhân phân số để tính nhanh:
\(\begin{array}{l}
M = \frac{8}{3}.\frac{2}{5}.\frac{3}{8}.10.\frac{{19}}{{92}}\\
N = \frac{5}{7}.\frac{5}{{11}} + \frac{5}{7}.\frac{2}{{11}} - \frac{5}{7}.\frac{{14}}{{11}}\\
Q = \left( {\frac{1}{{99}} + \frac{{12}}{{999}} - \frac{{13}}{{9999}}} \right).\left( {\frac{1}{2} - \frac{1}{3} - \frac{1}{6}} \right)
\end{array}\)
Lúc 6 giờ 50 phút bạn Việt đi xe đạp từ A đến B với vận tốc 15km/h. Lúc 7 giờ 10 phút ban Nam đi xe đạp từ B để đến A với vận tốc 12km/h. Hai bạn gặp nhau ở C lúc 7 giờ 30 phút. Tính quãng đường AB?
Khi giặt, vải bị co đi \(\frac{1}{{16}}\) theo chiều dài, và \(\frac{1}{{18}}\) theo chiều rộng. Hỏi phải mua bao nhiêu mét vải khổ 80cm để sau khi giặt có 17m2?
Tính các giá trị của biểu thức:
\(\begin{array}{l}
A = \frac{{{1^2}}}{{1.2}}.\frac{{{2^2}}}{{2.3}}.\frac{{{3^2}}}{{3.4}}.\frac{{{4^2}}}{{4.5}}\\
B = \frac{{{2^2}}}{{1.3}}.\frac{{{3^2}}}{{2.4}}.\frac{{{4^2}}}{{3.5}}.\frac{{{5^2}}}{{4.6}}
\end{array}\)
Tính nhanh:
\(M = \frac{2}{{3.5}} + \frac{2}{{5.7}} + \frac{2}{{7.9}} + ... + \frac{2}{{97.99}}\)
Trong các đẳng thức sau đây, đẳng thức minh họa tính chất kết hợp của phép nhân phân số là
\(\begin{array}{l}
\left( A \right)\frac{1}{3}.\frac{1}{5}.\frac{1}{2} = \frac{1}{3}.\frac{1}{2}.\frac{1}{5}\\
\left( B \right)\left( {\frac{1}{3}.\frac{1}{5}} \right).\frac{1}{2} = \frac{1}{3}.\left( {\frac{1}{5}.\frac{1}{2}} \right)\\
\left( C \right)\frac{1}{3}.\frac{1}{5} + \frac{1}{3}.\frac{1}{2} = \frac{1}{3}.\left( {\frac{1}{5} + \frac{1}{2}} \right)\\
\left( D \right)\frac{1}{3}.\frac{1}{5}.\frac{1}{2} = \left( {\frac{1}{3}.\frac{1}{5}} \right).\left( {\frac{1}{3}.\frac{1}{2}} \right)
\end{array}\)
Giá trị của biểu thức \(A = \frac{{ - 3}}{5}.\frac{1}{9} + \frac{2}{{15}}.\left( { - 7} \right) + \frac{{12}}{{ - 7}}.\frac{{ - 7}}{6}\) là:
(A) -2;
(B) 2;
(C) -1;
(D) 1;
Hãy chọn đáp án đúng.
Tính tích \(P = \left( {1 - \frac{1}{2}} \right)\left( {1 - \frac{1}{3}} \right)\left( {1 - \frac{1}{4}} \right)...\left( {1 - \frac{1}{{99}}} \right)\)
Chứng tỏ rằng \(\frac{1}{{101}} + \frac{1}{{102}} + ... + \frac{1}{{299}} + \frac{1}{{300}} > \frac{2}{3}\)
Tính tích \(A = \frac{3}{4}.\frac{8}{9}.\frac{{15}}{{16}}...\frac{{899}}{{900}}\)
Chứng tỏ rằng \(\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + ... + \frac{1}{{17}} < 2\)
Tính giá trị của biểu thức:
\(M = \frac{1}{{1.2.3}} + \frac{1}{{2.3.4}} + \frac{1}{{3.4.5}} + ...\frac{1}{{10.11.12}}\)
Tìm số nghịch đảo của các số sau:
a) -3
b) \(\frac{{ - 4}}{5}\)
c) -1
d) \(\frac{{13}}{{27}}\)
Tính giá trị của a, b, c, d rồi tìm nghịch đảo của chúng
\(\begin{array}{l}
a = \frac{1}{3} - \frac{1}{4}\\
b = \frac{2}{7}.\frac{{14}}{{15}} - 1\\
c = \frac{3}{4} - \frac{1}{{25}}.5\\
d = - 8.\left( {6.\frac{1}{{24}}} \right)
\end{array}\)
Tìm các cặp số nghịch đảo của nhau trong các cặp số sau:
a) 0,25 và 4
b) 3,4 và 4,3
c) 2 và 0,5
d) 0,7 và 7
Tìm x biết:
\(\begin{array}{l}
a)\frac{3}{4}x = 1\\
b)\frac{4}{7}x = \frac{9}{8} - 0,125
\end{array}\)
Tính tích rồi tìm số nghịch đảo của kết quả:
\(T = \left( {1 - \frac{1}{3}} \right)\left( {1 - \frac{1}{5}} \right)\left( {1 - \frac{1}{7}} \right)\left( {1 - \frac{1}{9}} \right)\left( {1 - \frac{1}{{11}}} \right)\left( {1 - \frac{1}{2}} \right)\left( {1 - \frac{1}{4}} \right)\left( {1 - \frac{1}{6}} \right)\left( {1 - \frac{1}{8}} \right)\left( {1 - \frac{1}{{10}}} \right)\)
Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2.
Viết số nghịch đảo của -2 dưới dạng tổng các nghịch đảo của ba số nguyên khác nhau.
Tính các thương sau rồi sắp xếp chúng theo thứ tự tăng dần:
\(\frac{3}{2}:\frac{9}{4};\frac{{48}}{{55}}:\frac{{12}}{{11}};\frac{7}{{10}}:\frac{7}{5};\frac{6}{7}:\frac{8}{7}\)
a) Một người đi bộ 12km trong 3 giờ. Hỏi trong 1 giờ, người ấy đi được bao nhiêu kilômét?
b) Một người đi xe đạp 8 km trong \(\frac{2}{3}\) giờ. Hỏi trong 1 giờ, người ấy đi được bao nhiêu kilômét?
Một bể đang chứa lượng nước bằng \(\frac{3}{4}\) dung tích bể. Người ta mở một vòi nước chảy vào bể, mỗi giờ chảy được \(\frac{1}{8}\) bể. Hỏi sau bao lâu thì bể đầy nước?
Một ô tô đi quãng đường AB với vận tốc 40km/h. Lúc về, xe đi quãng đường BA với vận tốc 50km/h. Thời gian cả đi lẫn về (không kể nghỉ) là 4 giờ 30 phút. Hỏi:
a) Thời gian ô tô đi 1 km lúc đi? Lúc về?
b) Thời gian ô tô đi và về 1km?
c) Độ dài quãng đường AB?
Viết phân số \(\frac{{14}}{{15}}\) dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có một chữ số
Tính giá trị của biểu thức:
\(A = \frac{{\frac{2}{3} + \frac{2}{5} - \frac{2}{9}}}{{\frac{4}{3} + \frac{4}{5} - \frac{4}{9}}}\)
Cho hai phân số \(\frac{8}{{15}}\) và \(\frac{18}{{35}}\) . Tìm phân số lớn nhất sao cho chia mỗi phân số này cho số đã cho ta được kết quả là số nguyên.
Tìm hai số, biết rằng \(\frac{9}{{11}}\) của số này bằng \(\frac{6}{{7}}\) của số kia và tổng của hai số đó bằng 258.
Số nghịch đảo của \(\frac{{ - 2}}{7}\) là:
\(\begin{array}{l}
\left( A \right)\frac{2}{7}\\
\left( B \right)\frac{7}{2}\\
\left( C \right)1\\
\left( D \right)\frac{{ - 7}}{2}
\end{array}\)
Hãy chọn đáp án đúng.
\(\frac{{12}}{{25}}\) là kết quả của phép chia:
\(\begin{array}{l}
\left( A \right)\frac{{ - 3}}{5}:\frac{5}{{ - 4}}\\
\left( B \right)\frac{2}{{25}}:6\\
\left( C \right)\frac{3}{{25}}:4\\
\left( D \right) - 6:\frac{{25}}{2}
\end{array}\)
Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho \(\frac{6}{7}\) và chia a cho \(\frac{10}{11}\) ta đều được kết quả là số tự nhiên.
Tích của hai phân số là \(\frac{3}{7}\) nếu thêm vào thừa số thứ nhất 2 đơn vị thì tích là \(\frac{13}{21}\). Tìm hai phân số đó.
Tìm hai số biết rằng \(\frac{7}{9}\) của số này bằng \(\frac{28}{33}\) của số kia và hiệu của hai số đó bằng 9.
Viết các số đo thời gian sau đây dưới dạng hỗn số và phân số với đơn vị là giờ:
1h15ph; 2h20ph; 3h12ph
Tính
\(\begin{array}{l}
a)6\frac{3}{8} + 5\frac{1}{2}\\
b)5\frac{3}{7} - 2\frac{3}{7}\\
c) - 5\frac{1}{7} + 3\frac{2}{5}\\
d) - 2\frac{1}{3} - 1\frac{2}{7}
\end{array}\)
Điền số thích hợp vào ô vuông:
Tìm x biết
\(\begin{array}{l}
a)0,5x - \frac{2}{3}x = \frac{7}{{12}}\\
b)x:4\frac{1}{3} = - 2,5\\
c)5,5x = \frac{{13}}{{15}}\\
d)\left( {\frac{{3x}}{7} + 1} \right):\left( { - 4} \right) = \frac{{ - 1}}{{28}}
\end{array}\)
Một người đi xe máy đoạn đường AB với vận tốc \(26\frac{1}{4}\) km/h hết 2,4 giờ. Lúc về, người ấy đi với vận tốc 30km/h. Tính thời gian người ấy đi từ B đến A?
Tìm y biết
\(\begin{array}{l}
a)y + 30\% y = - 1,3\\
b)y - 25\% y = \frac{1}{2}\\
c)3\frac{1}{3}y + 16\frac{3}{4} = - 13,25
\end{array}\)
Biết rằng tổng của mỗi hàng đều bằng 8,3 hãy điền số thích hợp vào các ô thay cho các chữ số a, b, c, d, e, g:
Viết các phân số dưới \(\frac{7}{{10}};\frac{{10}}{{21}};\frac{7}{8}\) dạng tổng các phân số có tử bằng 1 và mẫu khác nhau
Tính một cách hợp lý:
\(\begin{array}{l}
a)4\frac{3}{4} + \left( { - 0,37} \right) + \frac{1}{8} + \left( { - 1,28} \right) + \left( { - 2,5} \right) + 3\frac{1}{{12}}\\
b)\frac{3}{{5.7}} + \frac{3}{{7.9}} + ... + \frac{3}{{59.61}}\\
c)\frac{{\frac{5}{{22}} + \frac{3}{{13}} - \frac{1}{2}}}{{\frac{4}{{13}} - \frac{2}{{11}} + \frac{3}{2}}}
\end{array}\)
Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được kết quả đúng:
A) Hỗn số \(2\frac{3}{7}\) viết dưới dạng phân số là
B) Hỗn số \(-2\frac{3}{7}\) viết dưới dạng phân số là
C) Hỗn số \(-3\frac{2}{5}\) viết dưới dạng phân số là
D) Hỗn số \(5\frac{1}{7}\) viết dưới dạng phân số là
\(\begin{array}{l}
1)\frac{{ - 17}}{7}\\
2)\frac{{36}}{7}\\
3)\frac{{17}}{7}\\
4)\frac{{ - 13}}{5}\\
5)\frac{{ - 17}}{5}
\end{array}\)
Điền dấu x vào ô thích hợp trong bảng sau:
| Câu | Đúng | Sai |
| a) Hỗn số \( - 3\frac{1}{4}\) bằng \( - 3 + \frac{1}{4}\) | ||
| b) Hỗn số \(6\frac{2}{7}\) bằng \(\frac{{44}}{7}\) | ||
| c) Hỗn số \( - 10\frac{4}{5}\) bằng \( - 10 - \frac{4}{5}\) | ||
| d) Hỗn số \( - 3\frac{5}{8}\) bằng \(2\frac{5}{8}\) |
Tìm các phân số tối giản biết rằng: tích của tử và mẫu bằng 220; phân số tối giản đó có thể biểu diễn bởi một số thập phân
So sánh \(A = \frac{{{{20}^{10}} + 1}}{{{{20}^{10}} - 1}}\) và \(B = \frac{{{{20}^{10}} - 1}}{{{{20}^{10}} - 3}}\)
Tìm:
a) \(\frac{2}{5}\) của 40
b) \(\frac{5}{6}\) của 48 000 đồng
c) 4\(\frac{1}{2}\) của \(\frac{2}{5}\) kg
Có bao nhiêu phút trong:
a) \(\frac{1}{6}\) giờ
b) \(\frac{1}{3}\) giờ
c) \(\frac{3}{4}\) giờ
d) \(\frac{2}{5}\) giờ
e) \(\frac{7}{12}\) giờ
f) \(\frac{4}{15}\) giờ
Dùng số thập phân để biểu thị các số đo thời gian sau với đơn vị là giờ:
a) 3 giờ 30 phút
b) 2 giờ 15 phút
c) 0 giờ 45 phút
d) 6 giờ 12 phút
Biểu thị các số đo thời gian sau bằng giờ và phút:
a) 5,25 giờ
b) 10,5 giờ
c) 3,75 giờ
d) 2,1 giờ
e) 4,6 giờ
Một quả cam nặng 300g. Hỏi \(\frac{3}{4}\) quả cam nặng bao nhiêu?
Trên đĩa có 24 quả táo. Hạnh ăn 25% số táo. Sau đó Hoàng ăn \(\frac{4}{9}\) số táo còn lại. Hỏi trên đĩa còn mấy quả táo?
Một lớp có 45 học sinh bao gồm 3 loại: Giỏi, khá và trung bình. Số học sinh trung bình chiếm \(\frac{7}{{15}}\) số học sinh cả lớp. Số học sinh khá bằng \(\frac{5}{{8}}\) số học sinh còn lại. Tính số học sinh giỏi của lớp
Bốn thửa ruộng thu hoạch được tất cả 1 tấn thóc. Số thóc thu hoạch ở ba thửa ruộng đầu lần lượt bằng \(\frac{1}{4}\); 0,4 và 15% tổng số thóc thu hoạch ở cả bốn thửa. Tính khối lượng thóc thu hoạch được ở thửa thứ tư.
\(3\frac{4}{7}\) của 56 bằng:
(A) 168;
(B) 192 ;
(C) 200;
(D) 208.
Hãy chọn đáp án đúng.
Lớp 6A có 40 học sinh trong đó có 12,5% là học sinh giỏi. số học sinh giỏi của lớp 6A là
(A) 5;
(B) 6;
(C) 8;
(D) 10.
Hãy chọn đáp án đúng.
\(\frac{2}{5}\) của số a là 480. Tìm 12,5% của số a.
Một số có ba chữ số, chữ số hàng trăm là 4. Nếu chuyển chữ số 4 xuống sau chữ số hàng đơn vị thì được số mới bằng \(\frac{3}{4}\) số ban đầu. Tìm số ban đầu.
Tìm một số biết
a) \(\frac{2}{5}\)% của nó bằng 1,5
b) 3\(\frac{5}{8}\)% của nó bằng -5,8
\(\frac{2}{3}\) quả dưa hấu nặng 4\(\frac{1}{2}\)kg Hỏi quả dưa hấu nặng bao nhiêu kilôgam?
\(\frac{2}{3}\) số tuổi của Mai cách đây 3 năm là 6 tuổi. Hỏi hiện nay Mai bao nhiêu tuổi?
Bạn An đọc một cuốn sách trong ba ngày. Ngày thứ nhất đọc \(\frac{1}{3}\) số trang. Ngày thứ hai đọc \(\frac{5}{8}\) số trang còn lại. Ngày thứ ba đọc nốt 90 trang. Tính xem cuốn sách có bao nhiêu trang?
Một tấm vải bớt đi 8m thì còn lại \(\frac{7}{{11}}\) tấm vải. Hỏi tấm vải dài bao nhiêu mét?
Một người mang một rổ trứng đi bán. Sau khi bán \(\frac{4}{9}\) số trứng và 2 quả thì còn lại 28 quả. Tính số trứng mang đi bán.
Số sách ở ngăn A bằng \(\frac{3}{5}\) số sách ở ngăn B. Nếu chuyển 14 quyển từ ngăn B sang ngăn A thì số sách ở ngăn A bằng \(\frac{25}{23}\) số sách ở ngăn B. Tính số sách lúc đầu ở mỗi ngăn.
Khối 6 của một trường có 4 lớp. Số học sinh lớp 6A bằng \(\frac{9}{{25}}\) tổng số học sinh của ba lớp còn lại. Số học sinh lớp 6B bằng \(\frac{21}{{64}}\) tổng số học sinh ba lớp còn lại. Số học sinh lớp 6C bằng \(\frac{4}{{13}}\) tổng số học sinh ba lớp còn lại. Số học sinh lớp 6D là 43 bạn. Hỏi tổng số học sinh khối 6 của trường đó và số học sinh của mỗi lớp?
\(\frac{3}{7}\) của 28 thì bằng \(\frac{12}{7}\) của số:
(A) 7 ;
(B) 12 ;
(C) 4 ;
(D) \(\frac{36}{49}\).
Hãy chọn đáp án đúng.
\(\frac{1}{3}\)% của một số là 10. Số đó là:
(A) 0,03
(B) 0,3
(C) 3
(D) 3000
Hãy chọn đáp án đúng
Một người mang một sọt cam đi bán. Sau khi bán \(\frac{3}{7}\) số cam và 2 quả thì số cam còn lại là 45 quả. Tính số cam người ấy mang đi bán.
Hai đội công nhân sửa hai đoạn đường có chiều dài tổng cộng là 200m. Biết rằng \(\frac{1}{6}\) đoạn đường đội thứ nhất sửa bằng \(\frac{1}{4}\) đoạn đường đội thứ hai sửa. Tính chiều dài đoạn đường mỗi đội đã sửa.
Tìm tỉ số của hai số a và b, biết:
a) a = \(\frac{3}{5}\) m ; b = 70 cm
b) a = 0,2 tạ; b = 12 kg
Một người đi bộ một phút được 50m và một người đi xe đạp một giờ được 12km. Tính tỉ số vận tốc của người đi bộ và người đi xe đạp.
Năm nay con 12 tuổi, bố 42 tuổi. Tính tỉ số giữa tuổi con và tuổi bố.
a) Hiện nay;
b) Trước đây 7 năm;
c) Sau 28 năm.
Tìm tỉ số phần trăm của hai số:
a) \(2\frac{3}{7}\) và \(1\frac{13}{21}\)
b) 0,3 tạ và 50 kg
Trên một bản đồ tỉ lệ: 1000000, đoạn đường bộ từ Hà Nội đến Vinh dài 29cm. Tính độ dài đoạn đường đó trong thực tế.
Tỉ số của a và b là \(\frac{2}{7}\), tỉ số của 2 số b và c là \(\frac{21}{26}\). Tính tỉ số của hai số a và c.
Tỉ số của hai số bằng 2:7. Nếu thêm 35 vào số thứ nhất thì tỉ số của chúng sẽ bằng 11:14. Tìm hai số đó?
Tìm hai số, biết tỉ số của chúng bằng 2:5 và tích của chúng bằng 40.
Điền vào chỗ trống (…):
a) Tỉ số của \(\frac{3}{4}\) và 60cm là ……………….
b) Tỉ số của \(\frac{2}{5}\) giờ và 12 phút là…………..
c) Tỉ số của 2,5 tạ và 80 kg là ………..
d) Tỉ số của 2 ngày và 3\(\frac{1}{2}\) giờ là ……………
Nếu tăng một cạnh của hình chữ nhật thêm 10% độ dài của nó và giảm cạnh kia đi 10% độ dài của nó thì diện tích hình chữ nhật đó:
(A) Tăng lên 1%;
(B) Giảm đi 1%;
(C) Không thay đổi;
(D) Không kết luận được có thay đổi hay không.
Hãy chọn đáp án đúng
Một khu đất hình chữ nhật có diện tích là 5000m2. Trên bản đồ tỉ lệ xích 1:1000, khu đất đó có diện tích bao nhiêu?
Hiệu của hai số là 32. Biết 25% số lớn bằng 0,375 số nhỏ. Tìm hai số đó.
Tỉ số của hai số là \(\frac{3}{5}\) hiệu các bình phương của chúng -64. Tìm hai số đó
Tính tỉ số phần trăm của hai số:
a) 5 và 8
b) 10 và 7
c) 7 và 12
d) 13 và 6
Tính
a) 8% của 90
b) 7% của 80
c) 6% của 38
d) 3% của 97
a) Tỉ số tuổi anh và tuổi em là 150%. Em kém anh 4 tuổi. Tính tuổi anh và tuổi em.
b) Tỉ số của tuổi con và tuổi mẹ là 37,5%. Tổng số tuổi của hai mẹ con là 44. Tính tuổi mỗi người.
Lớp 6C có 48 học sinh. Số học sinh giỏi bằng 18,75% số học sinh cả lớp. Số học sinh trung bình bằng 300% số học sinh giỏi. Còn lại là học sinh khá.
a) Tính số học sinh mỗi loại của lớp 6C.
b) Tính tỉ số phần trăm số học sinh trung bình và số học sinh khá so với số học sinh cả lớp.
a) Tính khối lượng đường chứa trong \(\frac{3}{4}\) tấn sắn tươi biết rằng sắn tươi chứa 25% đường.
b) Muốn có 350kg đường thì phải dùng bao nhiêu kilôgam sắn tươi?
Kết quả tìm hiểu sở thích của 320 học sinh khối 6 cho biết: có đúng 62,5% số học sinh thích đá bóng; 43,2% thích đá cầu và 25% thích nhảy dây. Theo em, con số nào chắc chắn là không chính xác?
An nói với Bình: "Theo một cuộc điều tra của Đài truyền hình có 32% số người được hỏi ý kiến tán thành chiếu phim hoạt hình cho thiếu nhi vào tất cả các buổi tối". Bình nói ngay: "Như vậy tức là có 68% số người được hỏi ý kiến phản đối". Em nghĩ gì về câu nói của Bình.
Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được kết quả đúng:
A) 8% của 120 là
B) 12% của 36 là
C) 0,25% của 104 là
D) 67% của 5 là
1) 4,32
2) 2,6
3) 0,26
4) 9,6
5) 3,35
Chu vi một hình chữ nhật là 36m. nếu giảm chiều dài 20% của nó và tăng chiều rộng 25% của nó thì chu vi hình chữ nhật không đổi.
Hãy điền vào chỗ trống (…)
a) Chiều dài của hình chữ nhật đó là ……..
b) Chiều rộng hình chữ nhật đó là …………
c) Diện tích hình chữ nhật là ………….
Khối lượng công việc tăng 80% nhưng năng suất lao động chỉ tăng 20%. Hỏi phải tăng số công nhân thêm bao nhiêu phần trăm?
Tìm số nguyên x, biết:
\(4\frac{1}{3}\left( {\frac{1}{6} - \frac{1}{2}} \right) \le x \le \frac{2}{3}\left( {\frac{1}{3} - \frac{1}{2} - \frac{3}{4}} \right)\)
Tính
\(1\frac{{13}}{{15}}.0,75 - \left( {\frac{{104}}{{195}} + 25\% } \right).\frac{{24}}{{47}} - 3\frac{{12}}{{13}}:3\)
Tìm x, biết:
\(\left( {\frac{1}{{12}} + 3\frac{1}{6} - 30,75} \right)x - 8 = \left( {\frac{3}{5} + 0,415 + \frac{1}{{200}}} \right):0,01\)
So sánh
\(A = \frac{{{{10}^8} + 2}}{{{{10}^8} - 1}};B = \frac{{{{10}^8}}}{{{{10}^8} - 3}}\)
Chứng minh:
\(S = \frac{1}{5} + \frac{1}{{13}} + \frac{1}{{14}} + \frac{1}{{15}} + \frac{1}{{61}} + \frac{1}{{62}} + \frac{1}{{63}} < \frac{1}{2}\)
Một bác nông dân mang cam đi bán. Lần thứ nhất bán \(\frac{1}{2}\) số cam và \(\frac{1}{2}\) quả; lần thứ hai bán \(\frac{1}{3}\) số cam còn lại và \(\frac{1}{3}\) quả; lần thứ ba bán \(\frac{1}{4}\) số cam còn lại và \(\frac{3}{4}\) quả. Cuối cùng còn 24 quả cam. Hỏi số cam bác nông dân đã mang đi bán?
Phân số \(\frac{a}{b}\) sau khi rút gọn được phân số \(\frac{-8}{11}\). Biết b – a = 190, tìm phân số \(\frac{a}{b}\).
Tính \(A = \left( {\frac{{878787}}{{959595}} + \frac{{ - 8787}}{{9595}}} \right).\frac{{1234321}}{{5678765}}\)
Cho biểu thức:
\(\begin{array}{l}
A = \frac{{2009.2010 - 2}}{{2008 + 2008.2010}}\\
B = \frac{{ - 2009.20102010}}{{20092009.2010}}
\end{array}\)
Tính A + B
Tính giá trị của biểu thức
\(P = \frac{{2.3.4 - 2.3.4.9 + 2.3.4.11 - 2.3.4.13}}{{5.6.7 - 5.6.7.9 + 5.6.7.11 - 5.6.7.13}}\)
Chứng minh rằng: \(S = \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{20}}}} < 1\)
Có bao nhiêu cách viết phân số \(\frac{1}{5}\) dưới dạng tổng của hai phân số \(\frac{1}{a} + \frac{1}{b}\) với 0 < a < b?
Tìm số tự nhiên có hai chữ số sao cho tỉ số giữa số đó với tổng các chữ số của nó là lớn nhất.
Có thể tìm được hai chữ số a và b sao cho phân số \(\frac{a}{b}\) bằng số thập phân a,b hay không ?
Số liệu của ngành Giáo dục và Đào tạo năm học 1998 - 1999 cho biết: Cả nước ta có 5564888 học sinh THCS, trong đó có 2968868 học sinh nam . Dùng máy tính bỏ túi để tính tỉ số phần trăm của số học sinh nam và của số học sinh nữ so với tổng số học sinh THCS.
Copyright © 2021 HOCTAPSGK