Toán 11 Kết nối tri thức tập 1 trang 16

Giải Toán 11 Bài 1: Giá trị lượng giác của góc lượng giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 11 Kết nối tri thức với cuộc sống tập 1 trang 5→16.

Toán 11 Kết nối tri thức tập 1 trang 16 được biên soạn đầy đủ, chi tiết trả lời các câu hỏi từ bài 1.1 đến 1.6. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 tập 1 Bài 1 Giá trị lượng giác của góc lượng giác Kết nối tri thức, mời các bạn cùng theo dõi tại đây.

Giải Toán 11 Bài 1: Giá trị lượng giác của góc lượng giác

1. Toán 11 Kết nối tri thức tập 1 trang 16
2. Luyện tập Giá trị lượng giác của góc lượng giác

1. Toán 11 Kết nối tri thức tập 1 trang 16

Bài 1.1 trang 16

Hoàn thành bảng sau

Số đo độ	$15 ^{\circ}$	?	$0^{\circ}$	$900^{\circ}$	?	?
Số đo radian	?	$\frac{3\pi }{8}$	?	?	$-\frac{7\pi }{12}$	$-\frac{11\pi }{8}$

Gợi ý đáp án:

Số đo độ	$15 ^{\circ}$	$67.5^{\circ}$	$0^{\circ}$	$900^{\circ}$	$-105^{\circ}$	$-247.5^{\circ}$
Số đo radian	$\frac{\pi }{12}$	$\frac{3\pi }{8}$	0	$5\pi$	$-\frac{7\pi }{12}$	$-\frac{11\pi }{8}$

Bài 1.2 trang 16

Một đường tròn có bán kính 20 cm. Tìm độ dài của các cung trên đường tròn đó có số đo sau:

a) $\frac{\pi }{12}$

b) 1.5

c) $35^{\circ}$

d) $315^{\circ}$

Gợi ý đáp án:

a) Độ dài cung đường tròn: $l=20\times \frac{\pi }{12}=5.236$ (cm)

b) Độ dài cung đường tròn: $l=20\times 1.5=30$ (cm)

c) Đổi $35^{\circ}=\frac{7\pi }{36}$

Độ dài cung đường tròn: $l=20\times \frac{7\pi }{36}=12.2173$ (cm)

d) Đổi $315^{\circ}=\frac{7\pi }{4}$

Độ dài cung đường tròn: $l=20\times \frac{7\pi }{4}=109.9557$ (cm)

Bài 1.3 trang 16

Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:

a) $\frac{2\pi }{3}$

b) $-\frac{11\pi }{4}$

c) $150^{\circ}$

d) $315^{\circ}$

Gợi ý đáp án

a) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $\frac{2\pi }{3}$ được xác định trong hình sau:

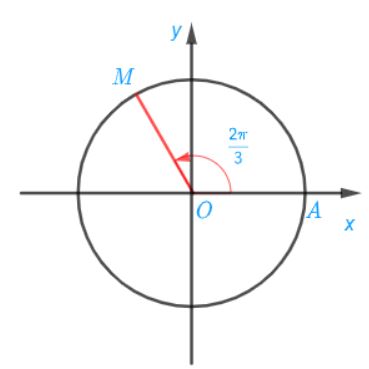
b) Ta có: $-\frac{11\pi }{4}=-(\frac{3\pi }{4}+2\pi )$

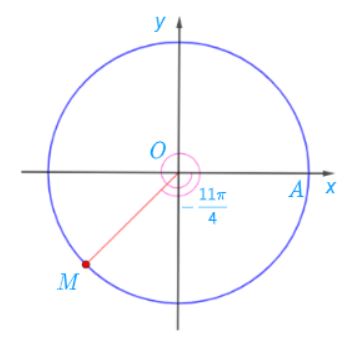
Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $-\frac{11\pi }{4}$ được xác định trong hình sau:

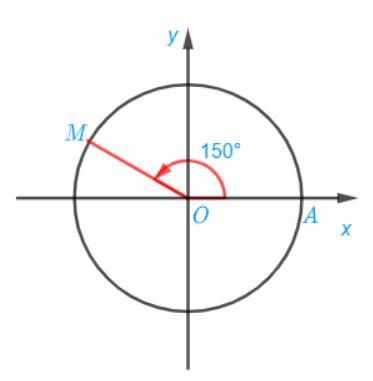
c) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng 150° được xác định trong hình sau:

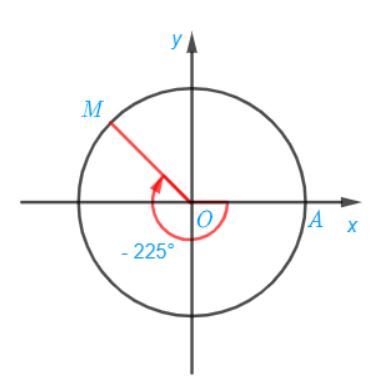
d) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng – 225° được xác định trong hình sau:

Bài 1.4 trang 16

Tính các giá trị lượng giác góc $\alpha$ , biết

a) $cos\alpha =\frac{1}{5} và 0<\alpha <\frac{\pi }{2}$

b) $sin\alpha =\frac{2}{3} và \frac{\pi }{2}<\alpha <\pi$

c) $tan\alpha =\sqrt{5} và \pi < \alpha <\frac{3\pi }{2}$

d) $cot\alpha =-\frac{1}{\sqrt{2}} và \frac{3\pi }{2}<\alpha <2\pi$

Gợi ý đáp án

a) Vì $0 < \alpha <\frac{\pi }{2}$ nên $sin \alpha > 0$

Mặt khác, từ $sin^{2}\alpha +cos^{2}\alpha =1$ suy ra $sin\alpha =\sqrt{1-cos^{2}\alpha }=\sqrt{1-\frac{1}{25}}=\frac{2\sqrt{6}}{5}$

Do đó, $tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{\frac{2\sqrt{6}}{5}}{\frac{1}{5}}=2\sqrt{6}$ và $cot\alpha =\frac{1}{tan\alpha }=\frac{1}{2\sqrt{6}}$

b) Vì $\frac{\pi }{2}<\alpha <\pi$ nên $cos\alpha<0$

Mặt khác, từ $sin^{2}\alpha +cos^{2}\alpha =1 suy ra cos\alpha =-\sqrt{1-sin^{2}\alpha }=-\sqrt{1-\frac{4}{9}}=-\frac{\sqrt{5}}{3}$

Do đó, $tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{\frac{2}{3}}{-\frac{\sqrt{5}}{3}}=-\frac{2\sqrt{5}}{5} và cot\alpha =\frac{1}{tan\alpha }=\frac{-\sqrt{5}}{2}$

c) $cot\alpha =\frac{1}{tan\alpha }=\frac{1}{2-\sqrt{5}}$

Vì $\pi < \alpha <\frac{3\pi }{2}$ nên $cos\alpha <0,sin\alpha <0$

Mặt khác, từ $1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }$ suy ra $cos\alpha =-\sqrt{\frac{1}{1+tan^{2}\alpha }}=-\sqrt{\frac{1}{1+5}}=-\frac{1}{\sqrt{6}}$

Từ $1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }$ suy ra $sin\alpha =-\sqrt{\frac{1}{1+cot^{2}\alpha }}=-\sqrt{\frac{1}{1+\frac{1}{5}}}=-\frac{\sqrt{30}}{6}$

d) $tan\alpha =\frac{1}{cot\alpha }=-\sqrt{2}$

Vì $\frac{3\pi }{2}<\alpha <2\pi$ nên $cos\alpha >0,sin\alpha <0$

Mặt khác, từ $1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }$ suy ra $cos\alpha =\sqrt{\frac{1}{1+tan^{2}\alpha }}=\sqrt{\frac{1}{1+2}}=\frac{1}{\sqrt{3}}$

Từ $1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }$ suy ra $sin\alpha =-\sqrt{\frac{1}{1+cot^{2}\alpha }}=-\sqrt{\frac{1}{1+\frac{1}{2}}}=-\frac{\sqrt{6}}{3}$

Bài 1.5 trang 16

Chứng minh các đẳng thức:

a) $cos^{4}\alpha -sin^{4}\alpha =2cos^{2}\alpha -1$

b) $\frac{cos^{2}\alpha +tan^{2}\alpha -1}{sin^{2}\alpha }=tan^{2}\alpha$

Gợi ý đáp án

a) $cos^{4}\alpha -sin^{4}\alpha =(cos^{2}\alpha +sin^{2}\alpha )(cos^{2}\alpha -sin^{2}\alpha )$

$=1\times (cos^{2}\alpha -sin^{2}\alpha )=cos^{2}\alpha -(1-sin^{2}\alpha )=2cos^{2}\alpha -1$

b) $\frac{cos^{2}\alpha +tan^{2}\alpha -1}{sin^{2}\alpha }=\frac{cos^{2}\alpha }{sin^{2}\alpha }+\frac{tan^{2}\alpha }{sin^{2}\alpha }-\frac{1}{sin^{2}\alpha }$