Toán 8 Thực hiện tính toán trên đa thức với phần mềm GeoGebra là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Kết nối tri thức với cuộc sống tập 1 trang 113, 114.

Giải Toán 8 Kết nối tri thức tập 1 trang 113, 114 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập bài Thực hiện tính toán trên đa thức với phần mềm GeoGebra - Hoạt động thực hành trải nghiệm. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Giải Toán 8 Kết nối tri thức Tập 1 trang 113, 114

Sử dụng phần mềm GeoGebra, hãy thực hiện các yêu cầu sau đây.

Bài 1

Tính: 

Lời giải:

Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

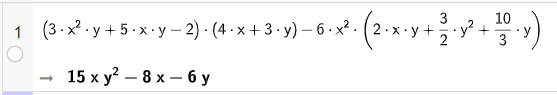
Bài 2

Khai triển các biểu thức sau:

a) (5x – y)²;

b)

Lời giải:

a) Khai triển biểu thức (5x – y)²:

• Sử dụng lệnh Expand(<biểu thức cần khai triển>).

• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

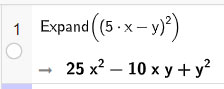
Vậy (5x – y)² = 25x² – 10xy + y².

b) Khai triển biểu thức  

• Sử dụng lệnh Expand(<biểu thức cần khai triển>).

• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

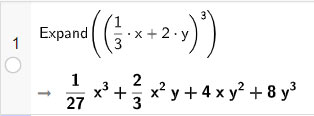
Vậy  

Bài 3

Phân tích các đa thức sau thành nhân tử:

a) x⁴ – 4x³ – 7x² + 8x + 10;

b) (x + y + z)³ – x³ – y³ – z³.

Lời giải:

a) Phân tích các đa thức x⁴ – 4x³ – 7x² + 8x + 10 thành nhân tử:

• Sử dụng lệnh Factor(<đa thức>) (hoặc Factorise(<đa thức>)).

• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

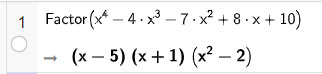
Vậy x⁴ – 4x³ – 7x² + 8x + 10 = (x – 5)(x + 1)(x² – 2).

b) Phân tích các đa thức (x + y + z)³ – x³ – y³ – z³ thành nhân tử:

• Sử dụng lệnh Factor(<đa thức>) (hoặc Factorise(<đa thức>)).

• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

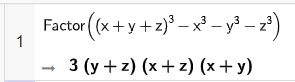
Vậy (x + y + z)³ – x³ – y³ – z³ = 3(y + z)(x + z)(x + y).

Bài 4

Tìm thương và dư (nếu có) trong các phép chia sau:

a) (3x⁴y – 9x³y² – 21x²y²) : (3x²y);

b) (2x³ + 5x² – 2x + 12) : (2x² – x + 1).

Lời giải:

a) Tìm thương và dư (nếu có) trong các phép chia (3x⁴y – 9x³y² – 21x²y²) : (3x²y).

• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.

• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

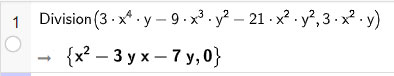
Vậy phép chia hai đa thức (3x⁴y – 9x³y² – 21x²y²) cho (3x²y), ta được thương là x² – 3xy – 7y và dư 0.

b) Tìm thương và dư (nếu có) trong các phép chia (2x³ + 5x² – 2x + 12) : (2x² – x + 1).

• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.

• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

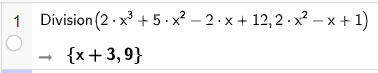
Vậy phép chia hai đa thức (2x³ + 5x² – 2x + 12) cho (2x² – x + 1), ta được thương là x + 3 và dư 9.