Bài 1 (2,0 điểm)

1) Tìm giá trị của x để các biểu thức có nghĩa:

2) Rút gọn biểu thức:

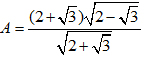
Bài 2 (2,0 điểm)

Cho phương trình: mx² – (4m - 2)x + 3m – 2 = 0 (1) (m là tham số).

1) Giải phương trình (1) khi m = 2.

2) Chứng minh rằng phương trình (1) luôn có nghiệm với mọi giá trị của m.

3) Tìm giá trị của m để phương trình (1) có các nghiệm là nghiệm nguyên.

Bài 3 (2,0 điểm)

Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Một mảnh vườn hình chữ nhật có chu vi 34m. Nếu tăng thêm chiều dài 3m và chiều rộng 2m thì diện tích tăng thêm 45m². Hãy tính chiều dài, chiều rộng của mảnh vườn.

Bài 4 (3,0 điểm)

Cho đường tròn O. Từ A là một điểm nằm ngoài (O) kẻ các tiếp tuyến AM và AN với (O) (M; N là các tiếp điểm).

1) Chứng minh rằng tứ giác AMON nội tiếp đường tròn đường kính AO.

2) Đường thẳng qua A cắt đường tròn (O) tại B và C (B nằm giữa A và C). Gọi I là trung điểm của BC. Chứng minh I cũng thuộc đường tròn đường kính AO.

3) Gọi K là giao điểm của MN và BC. Chứng minh rằng AK.AI = AB.AC.

Bài 5 (1,0 điểm)

Cho các số x,y thỏa mãn x ≥ 0; y ≥ 0 và x + y = 1.

Tìm giả trị lớn nhất và nhỏ nhất của A = x² + y².

Download tài liệu để xem thêm chi tiết.