Bài 1: (2,0 điểm) (không dùng máy tính cầm tay)

1. Chứng minh:

2. Cho biểu thức: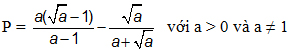

Rút gọn rồi tính giá trị của P tại a = 2014²

Bài 2: (2,0 điểm)

1. Tìm x biết:

2. Giải hệ phương trình: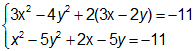

Bài 3: (2,0 điểm)

Trong mặt phẳng tọa độ Oxy, cho parapol

1. Vẽ đồ thị (P)

2. Gọi M là điểm thuộc (P) có hoành độ x = 2. Lập phương trình đường thẳng đi qua điểm M đồng thời cắt trục hoành và trục tung lần lượt tại hai điểm phân biệt A và B sao cho diện tích tam giác OMA gấp đôi diện tích tam giác OMB.

Bài 4: (4,0 điểm)

Cho đường tròn (O; 3cm) có hai đường kính AB và CD vuông góc với nhau. Gọi M là điểm tùy ý thuộc đoạn OC (M khác O và C). Tia BM cắt đường tròn (O) tại N

1. Chứng minh AOMN là một tứ giác nội tiếp

2. Chứng minh ND là phân giác của góc ANB

3. Tính

4. Gọi E và F lần lượt là hai điểm thuộc các đường thẳng AC và AD sao cho M là trung điểm của EF. Nếu cách xác định các điểm E, F và chứng minh rằng tổng (AE + AF) không phụ thuộc vào vị trí của điểm M.

Download tài liệu để xem thêm chi tiết