Đường trung bình của tam giác là gì? Cách tính đường trung bình như thế nào? Mời quý thầy cô cùng các bạn học sinh lớp 8 theo dõi bài viết dưới đây.
Đường trung bình là tài liệu hữu ích được biên soạn đầy đủ lý thuyết về khái niệm, công thức tính và các định lý đường trung bình. Qua đó giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được điểm số cao trong kì thi học kì môn Toán 8. Vậy sau đây là nội dung chi tiết tài liệu đường trung bình tam giác mời các bạn cùng theo dõi tại đây. Bên cạnh đó các bạn xem thêm Đường cao trong tam giác cân.
Đường trung bình của tam giác
1. Đường trung bình của tam giác
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
2. Định lí đường trung bình của tam giác
- Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
- Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Ví dụ: Cho Δ ABC có M là trung điểm của AB, N là trung điểm của AC và BC = 4cm. Tính độ dài MN.
Lời giải:
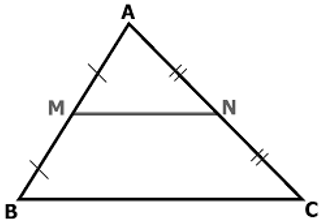
Xét tam giác ABC có: M là trung điểm của AB (gt), N là trung điểm của AC (gt)
⇒ MN là đường trung bình của Δ ABC (định lý)
Áp dụng định lý 2, ta có ![]()
⇒ ![]() (cm)
(cm)
3. Bài tập đường trung bình của tam giác
Bài 1: Cho tam giác ABC (AB > AC) có ![]() . Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E, F lần lượt là trung điểm của cạnh AD, BC. Tính
. Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E, F lần lượt là trung điểm của cạnh AD, BC. Tính ![]() ?
?
Lời giải:
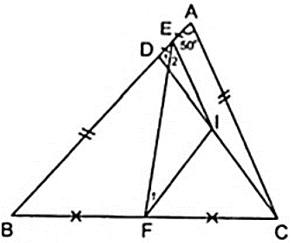
+ Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác BCD và ACD.
+ Đặt BD = AC = 2a
Áp dụng định lý đường trung bình của hai tam giác trên ta có:
(1) FI//BD (2) FI = a
(3) EI = a (4) EI//AC
Từ (1) ⇒ ![]() (ở vị trí so le trong) (5)
(ở vị trí so le trong) (5)
Từ (2) và (3) ⇒ FI = EI nên ![]() (vì trong tam giác, đối diện với hai cạnh bằng nhau là hai góc bằng nhau) (6)
(vì trong tam giác, đối diện với hai cạnh bằng nhau là hai góc bằng nhau) (6)
Từ (5) và (6) ⇒ ![]()
Từ (4) ⇒ ![]() (ở vị trí đồng vị)
(ở vị trí đồng vị)
Mà ![]()
Bài 2
Cho hình sau. Chứng minh rằng AI = IM.
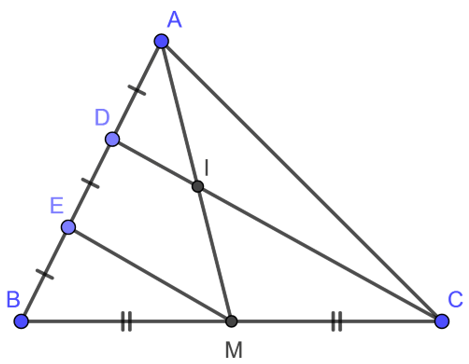
Gợi ý đáp án
Xét tam giác BCD có:
E là trung điểm của BD
M là trung điểm của BC
Suy ra, EM là đường trung bình của tam giác BDC
![]()
Xét tam giác AEM có:
D là trung điểm của AE
DI // EM
Suy ra, I là trung điểm của AM
Hay AI = IM (đpcm)
