Bài tập về đường trung trực của một đoạn thẳng là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh tham khảo.

Bài tập về đường trung trực lớp 7 bao gồm 12 trang tổng hợp toàn bộ kiến thức lý thuyết trọng tâm, các dạng toán và bài tập chuyên đề tính chất đường trung trực của một đoạn thẳng, có đáp án và lời giải chi tiết kèm theo. Tài liệu này phù hợp với 3 bộ sách giáo khoa Toán 7 theo chương trình mới. Vậy sau đây là nội dung chi tiết trọn bộ tài liệu đường trung trực lớp 7 mời các bạn cùng đón đọc.

I. Kiến thức đường trung trực của đoạn thẳng

1. Đường trung trực là gì

Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.

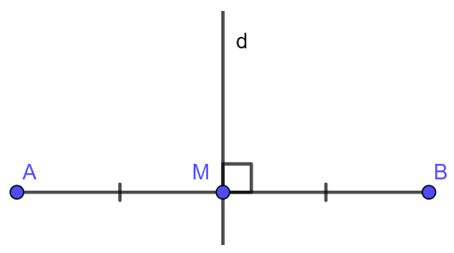
Hình vẽ trên, d là đường trung trực của đoạn thẳng AB.

2. Tính chất

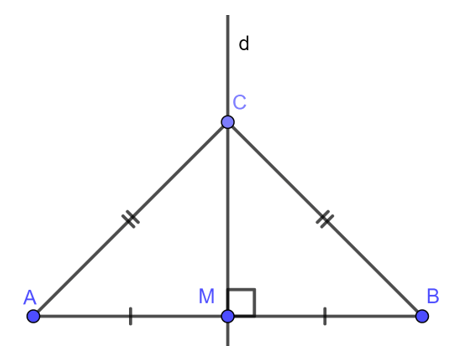
• Định lí 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

d là đường thẳng trung trực của đoạn thẳng AB, Trung trực của đoạn thẳng là gì

• Định lí 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

d là đường trung trực của đoạn thẳng AB. Ta có: CA = CB suy ra điểm C thuộc đường thẳng d.

• Nhận xét: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.

Ví dụ: Cho tam giác ABC, hãy tìm một điểm O cách đều ba điểm A, B, C của tam giác ABC.

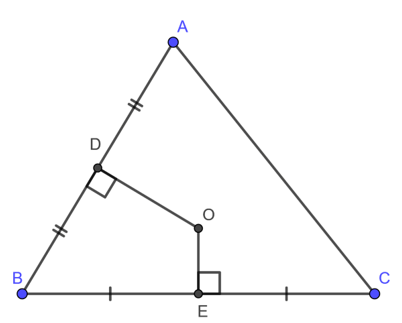
Hướng dẫn:

Trung trực của đoạn thẳng là gì

Ta có:

Điểm O cách đều hai điểm A, B nên suy ra điểm O nằm trên đường trung trực của đoạn thẳng AB.

Điểm O cách đều hai điểm B, C nên suy ra điểm O nằm trên đường trung trực của đoạn thẳng BC.

Điểm O cách đều ba điểm A, B, C nên suy ra O là giao điểm của ba đường trung trực của tam giác ABC.

II. Các dạng bài tập đường trung trực lớp 7

Dạng 1: Vận dụng tính chất của đường trung trực.

Sử dụng định lí 1: “Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó”.

Dạng 2: Chứng minh một điểm thuộc đường trung trực. Chứng minh một đường thẳng là đường trung trực của một đoạn thẳng.

– Để chứng minh điểm M thuộc đường trung trực của đoạn thẳng AB, ta dùng định lí 2: “Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó” hoặc dùng định nghĩa đường trung trực.

– Để chứng minh đường thẳng d là đường trung trực của đoạn thẳng AB, ta chứng minh d chứa hai điểm cách đều A và B, hoặc dùng định nghĩa đường trung trực.

Dạng 3: Xác định vị trí của điểm thỏa mãn yêu cầu đề bài.

Sử dụng định lí 2: “Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó” để xác định một điểm nằm trên đường trung trực của đoạn thẳng.

Dạng 4: Sử dụng tính chất đường trung trực vào bài toán về cực trị.

– Sử dụng tính chất đường trung trực để thay đổi độ dài một đoạn thẳng bằng độ dài một đoạn thẳng khác bằng nó.

– Sử dụng bất đẳng thức tam giác để tìm giá trị nhỏ nhất, giá trị lớn nhất.