Câu 1: (2,5 điểm)

1. Cho biểu thức:

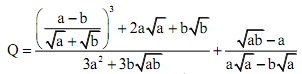
với a > 0, b > 0, a ≠ b. Chứng minh giá trị của biểu thức Q không phụ thuộc vào a và b.

2. Các số thức a, b, c thỏa mãn a + b + c = 0.

Chứng minh đẳng thức: (a² + b² + c²)² = 2(a⁴ + b⁴ + c⁴).

Câu 2: (2,0 điểm)

Cho parabol (P): y = x² và đường thẳng (tham số m ≠ 0)

1. Chứng minh rằng với mỗi m ≠ 0, đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt.

2. Gọi A(x₁, y₁), B(x₂, y₂) là các giao điểm của (d) và (P). Tìm giá trị nhỏ nhất của biểu thức: M = y₁² + y₂².

Câu 3: (1,5 điểm)

Giả sử a, b, c là các số thực, a ≠ b sao cho hai phương trình: x² + ax + 1 = 0, x² + bx + 1 = 0 có nghiệm chung và hai phương trình x² + x + a = 0, x² + cx + b = 0 có nghiệm chung. Tính: a + b + c.

Câu 4: (3,0 điểm)

Cho tam giác ABC không cân, có ba góc nhọn, nội tiếp đường tròn (O). Các đường cao AA₁, BB₁, CC₁ của tam giác ABC cắt nhau tại H, các đường thẳng A₁C₁ và AC cắt nhau tại điểm D. Gọi X là giao điểm thứ hai của đường thẳng BD với đường tròn (O).

1. Chứng minh: DX.DB = DC₁.DA₁.

2. Gọi M là trung điểm của cạnh AC. Chứng minh: DH vuông góc BM.

Câu 5: (1,0 điểm)

Các số thực x, y, x thỏa mãn:

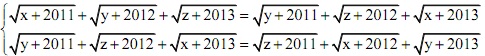
Chứng minh: x = y = z.

Download tài liệu để xem chi tiết.