Tứ giác nội tiếp đường tròn lớp 9 là một phần rất quan trọng trong chương trình THCS được ứng dụng nhiều trong các bài toán hình học phẳng lớp 9.
Tài liệu tổng hợp kiến thức lý thuyết kèm theo các dạng phương pháp kèm theo bài tập chuyên đề tứ giác nội tiếp đường tròn. Đây là tài liệu cực kì hữu ích đối với các em học sinh lớp 9 chuẩn bị thi vào lớp 10. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.
Tứ giác nội tiếp đường tròn
I. Khái niệm tứ giác nội tiếp đường tròn
Tứ giác nội tiếp trong một đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn.
II. Dấu hiệu nhận biết tứ giác nội tiếp được trong một đường tròn
1/ Nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được trong một đường tròn.
2/: Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó thì nội tiếp được trong một đường tròn.
3/: Tứ giác có 4 đỉnh cách đều một điểm ( mà ta có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
4/: Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc (an-pha) thì nội tiếp được trong một đường tròn.
III. Cách chứng minh tứ giác nội tiếp đường tròn
1) Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
Ví dụ: Cho tứ giác ABCD và điểm I
Tứ giác ABCD là tứ giác nội tiếp đường tròn tâm I
⇔ IA=IB=IC=ID
2) Chứng minh tứ giác có tổng 2 góc đối bằng 180°
Ví dụ: Cho tứ giác ABCD Tứ giác ABCD là tứ giác nội tiếp nếu góc A + góc C = 180° hoặc góc B + góc D = 180°
3) Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau
Ví dụ: Cho tứ giác ABCD Tứ giác ABCD là tứ giác nội tiếp ⇔ góc DAC = góc DBC cùng chắn cung DC
4) Nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được trong một đường tròn
Ví dụ: Cho tứ giác ABCD
Tứ giác ABCD là tứ giác nội tiếp ⇔ góc A + góc C = góc B + góc D. Đây là trường hợp đặc biệt của cách thứ 2.
5) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó thì nội tiếp được trong một đường tròn
Ví dụ: Cho tứ giác ABCD. Tứ giác ABCD là tứ giác nội tiếp nếu góc ngoài đỉnh A bằng góc C, hoặc góc ngoài đỉnh B bằng góc D.
6) Chứng minh bằng phương pháp phản chứng
Với cách này, các em chứng minh tứ giác là các hình đặc biệt như hình vuông, hình chữ nhật, hình thoi, hình bình hành.
IV. Một số bài toán luyện tập
1/ Dạng áp dụng dấu hiệu 1 & 4
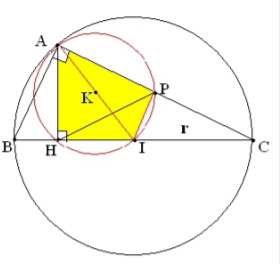
Bài 1: Cho tam giác ABC vuông tại A ( AB< AC ) nội tiếp trong đường tròn tâm I; bán kính r.
Gọi P là trung điểm của AC; AH là đường cao của tam giác ABC.
a/ Chứng minh tứ giác APIH nội tiếp được trong đường tròn tâm K. Xác định tâm K của đường tròn này.
b/ Chứng minh hai đường tròn ( I ) và ( K ) tiếp xúc nhau.
GỢI Ý
a/ Dựa vào dấu hiệu 1 để chứng minh APIH nội tiếp được trong một đường tròn:
- Xác định tâm K đường tròn ngoại tiếp tứ giác APIH: Điểm P nhìn đoạn thẳng AI dưới một góc vuông nên P thuộc đường tròn đường kính AI. Chứng minh tương tự đối với điểm H. Từ đó xác định được tâm K ( là trung điểm đoạn AI ).
(HS cần nắm lại kết luận sau: Quỹ tích các điểm nhìn đoạn thẳng AB dưới một góc vuông là đường tròn đường kính AB – SGK lớp 9/ tập 2 trang 85)
b/ Nhắc lại kiến thức về hai đường tròn tiếp xúc nhau:
- Hai đường tròn cùng đi qua chỉ có 1 điểm duy nhất thì chúng tiếp xúc với nhau; hoặc TX trong, hoặc TX ngoài.
- Tiếp xúc ngoài nếu khoảng cách hai tâm bằng tổng hai bán kính. OO’ = R + r
- Tiếp xúc trong nếu khoảng cách hai tâm bằng hiệu hai bán kính. OO’ = R – r> 0
- Tính IK để kết luận 2 đường tròn (I) và ( K ) tiếp xúc trong tại A.
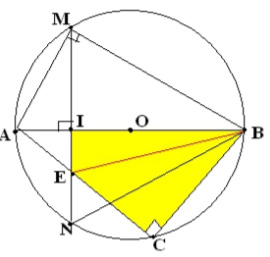
Bài 2: Cho đường tròn tâm O, đường kính AB cố định. Điểm I nằm giữa A và O sao cho AI = IO.
Kẻ dây MN ^AB tại I. Gọi C là một điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC, cắt MN tại E.
a/ Chứng minh tứ giác IECB nội tiếp được trong 1 đường tròn. Xác định tâm đường tròn này.
b/ Chứng minh tam giác AME đồng dạng với tam giác ACM.
GỢI Ý
a/ Chứng minh tương tự câu a ở bài 1 trên. (Góc ACB chắn đườngkính AB; MI^AB)
Tâm đường trong nội tiép IECB nằm tại trung điểm EB
Câu b/ Hai TG đó có chung góc A, góc AME và ACM chắn 2 cung AM = cung AN
................
Tải file tài liệu để xem thêm nội dung chi tiết
