ÔN THI ĐẠI HỌC MÔN TOÁN CHUYÊN ĐỀ: LƯỢNG GIÁC

VẤN ĐỀ 1: PHƯƠNG TRÌNH LƯỢNG GIÁC

A. PHƯƠNG PHÁP GIẢI

I. Phương trình lượng giác cơ bản

* cosx = cosα ↔ x = ± α + k2π

*

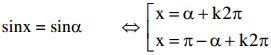
* tanx = tanα ↔ x = α + kπ

* cotx = cotα ↔ x = α + kπ

Với k thuộc Z

II. Phương trình bậc hai đối với một hàm số lượng giác

* asin²x + bsinx + c = 0. Đặt t = sinx, |t| ≤ 1

* acos²x + bcosx + c = 0. Đặt t = cosx, |t| ≤ 1

* atan²x + btanx + c = 0. Đặt t = tanx

* acot²x + bcotx + c = 0. Đặt t = cotx

III. Phương trình bậc nhất đối với sinx, cosx

asinx + bcosx = c (*)

Điều kiện có nghiệm: a² + b² ≥ c²

Cách 1:

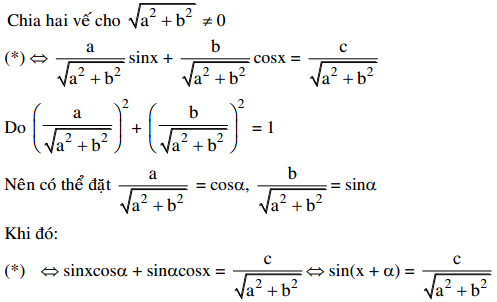
Cách 2:

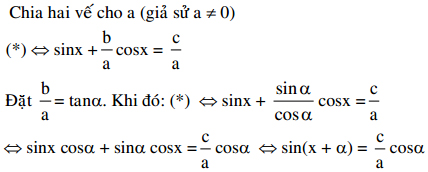
Cách 3:

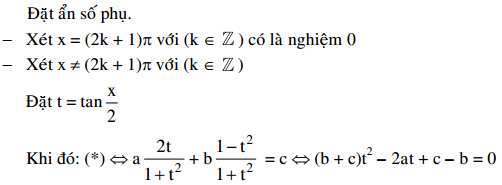
IV. Phương trình đối xứng: a(sinx + cosx) + bsinxcosx + c = 0

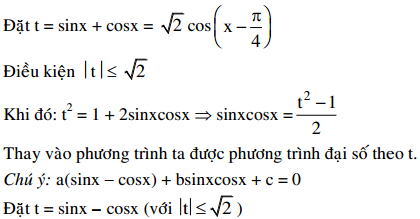
V. Phương trình đẳng cấp bậc 2 đối với sinx, cosx

asin²x + bsinxcosx + ccos²x = 0

- Xét cosx = 0 ↔ x = π/2 + kπ (k thuộc Z) có là nghiệm không?

- Xét cosx # 0. Chia 2 vế cho cos2x ta thu được phương trình bậc 2 theo tanx.

Chú ý: Nếu là phương trình đẳng cấp bậc k đối với sinx, cosx thì ta xét cosx = 0 và xét cosx # 0 chia 2 vế của phương trình cho cos^kx và ta thu được một phương trình bậc k theo tanx

B. ĐỀ THI

Bài 1: Đại học khối A năm 2011

Giải phương trình:c

Giải:

Điều kiện: sinx # 0. Khi đó:

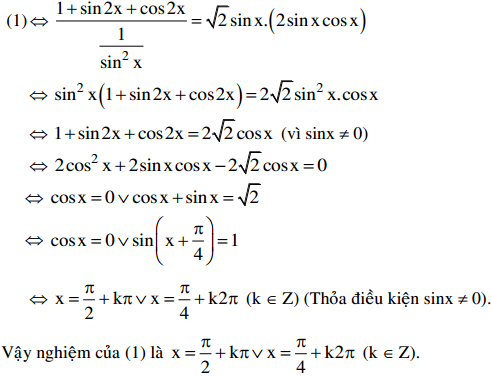
Bài 2: Đại học khối B năm 2011

Giải phương trình: sin2x.cosx + sinx.cosx = cos2x + sinx + cosx

Giải:

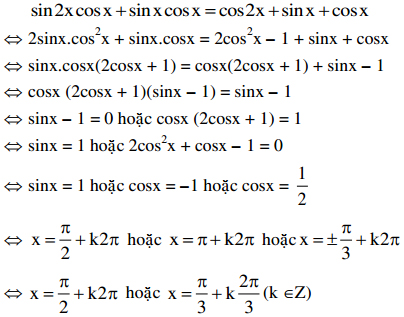
Bài 3: Đại học khối D năm 2011

Giải phương trình: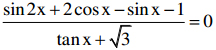

Download tài liệu để xem chi tiết.