Giải Toán 9 trang 7 - SGK Toán 9 Tập 2

Giải Toán lớp 9 trang 7 tập 2 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và bài tập trong SGK bài 1 Phương trình bậc nhất hai ẩn.

Giải Toán 9 Bài 1 trang 7 tập 2 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 7 tập 2 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Giải Toán 9 Bài 1: Phương trình bậc nhất hai ẩn

Trả lời câu hỏi phần nội dung bài học
- Câu hỏi 1
- Câu hỏi 2
Giải bài tập Toán 9 trang 7 tập 2
Lý thuyết Bài 1: Phương trình bậc nhất hai ẩn

Trả lời câu hỏi phần nội dung bài học

Câu hỏi 1

a. Kiểm tra xem các cặp số (1; 1) và (0,5; 0) có là nghiệm của phương trình 2x – y = 1 hay không?

b. Tìm thêm một nghiệm khác của phương trình 2x – y = 1.

Lời giải chi tiết

a. + Với $\left( 1;1 \right)\Rightarrow x=1,y=1$ thay vào phương trình ta được $2.1-1=1$

Vậy $\left( 1,1 \right)$ là nghiệm của phương trình.

+ Với $\left( 0,5;0 \right)\Rightarrow x=0,5,y=0$ thay vào phương trình ta được $2.0,5-0=1$

Vậy $\left( 0,5;0 \right)$ là nghiệm của phương trình.

b. Chọn x = 3 suy ra y = 6 – 1 = 5. Vậy (3; 5) là nghiệm của phương trình.

Chọn x = 4 suy ra y = 2.4 – 1 = 7. Vậy (4, 7) là nghiệm của phương trình.

Câu hỏi 2

Nêu nhận xét về số nghiệm của phương trình 2x – 1 = 1

Lời giải chi tiết

Áp dụng quy tắc chuyển vế ta có:

$2x-y=1\Rightarrow y=2x-1$

Nhận thấy với mỗi giá trị của x ta thu được một giá trị của y tương ứng. Số nghiệm của phương trình được biểu diễn bằng các điểm thuộc đường thẳng y = 2x – 1.

Vậy phương trình có vô số nghiệm

Giải bài tập Toán 9 trang 7 tập 2

Bài 1 (trang 7 SGK Toán 9 Tập 2)

Trong các cặp số (-2; 1), (0; 2), (-1; 0), (1, 5; 3) và (4; -3) cặp số nào là nghiệm của phương trình:

a) 5x + 4y = 8? ;

b) 3x + 5y = -3?

Xem gợi ý đáp án

a) Xét cặp (-2; 1). Thay x = -2 ; y = 1 vào phương trình 5x + 4y = 8 ta được :

5x + 4y = 5.(-2) + 4.1 = -10 + 4 = -6 ≠ 8

⇒ cặp số (-2; 1) không là nghiệm của phương trình 5x + 4y = 8.

Xét cặp(0; 2). Thay x = 0 ; y = 2 vào phương trình 5x + 4y = 8 ta được

5x + 4y = 5.0 + 4.2 = 8

⇒ cặp số (0; 2) là nghiệm của phương trình 5x + 4y = 8.

Xét cặp (-1; 0). Thay x = -1 ; y = 0 vào phương trình 5x - 4y = 8 ta được:

5x + 4y = 5.(-1) + 4.0 = -5 ≠ 8

⇒ cặp số (-1; 0) không là nghiệm của phương trình 5x + 4y = 8.

Xét cặp (1,5 ; 3). Thay x = 1,5 ; y = 3 vào phương trình 5x + 4y = 8 ta được

5x + 4y = 5.1,5 + 4.3 = 7,5 + 12 = 19,5 ≠ 8

⇒ (1,5; 3) không là nghiệm của phương trình 5x + 4y = 8.

Xét cặp (4;-3).Thay x = 4 ; y = -3 vào phương tình 5x + 4y = 8 ta được:

5x + 4y = 5.4 + 4.(-3) = 20 – 12 = 8

⇒ (4; -3) là nghiệm của phương trình 5x + 4y = 8.

Vậy có hai cặp số (0; 2) và (4; -3) là nghiệm của phương trình 5x + 4y = 8.

b) Xét cặp số (-2; 1).Thay x = -2 ; y = 1 vào phương trình 3x + 5y = -3 ta được:

3x + 5y = 3.(-2) + 5.1 = -6 + 5 = -1 ≠ -3

⇒ (-2; 1) không là nghiệm của phương trình 3x + 5y = -3.

Xét cặp số (0; 2) . Thay x = 0 ; y = 2 vào phương trình 3x + 5y = -3 ta được:

3x + 5y = 3.0 + 5.2 = 10 ≠ -3

⇒ (0; 2) không là nghiệm của phương trình 3x + 5y = -3.

Xét cặp (-1; 0).Thay x = -1 ; y = 0 vào phương trình 3x + 5y = -3 ta được:

3x + 5y = 3.(-1) + 5.0 = -3

⇒ (-1; 0) là nghiệm của phương trình 3x + 5y = -3. .

Xét cặp (1,5; 3). Thay x = 1,5 ; y = 3 vào phương trình 3x + 5y = -3 ta được:

3x + 5y = 3.1,5 + 5.3 = 4,5 + 15 = 19,5 ≠ -3

⇒ (1,5; 3) không là nghiệm của phương trình 3x + 5y = -3.

Xét cặp (4; -3). Thay x = 4 ; y = -3 vào phương trình 3x + 5y = -3 ta được:

3x + 5y = 3.4 + 5.(-3) = 12 – 15 = -3

⇒(4; -3) là nghiệm của phương trình 3x + 5y = -3.

Vậy có hai cặp số (-1; 0) và (4; -3) là nghiệm của phương trình 3x + 5y = -3.

Bài 2 (trang 7 SGK Toán 9 Tập 2)

Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:

a) 3x – y = 2;

b) x + 5y = 3;

c) 4x – 3y = -1;

d) x + 5y = 0 ;

e) 4x + 0y = -2 ;

f) 0x + 2y = 5.

Xem gợi ý đáp án

a) 3x – y = 2;

Ta có phương trình $3x - y = 2 \Leftrightarrow y=3x -2$ . Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x \in R & & \\ y = 3x - 2 & & \end{matrix}\right.$

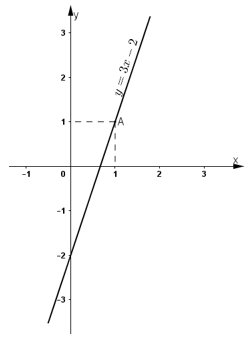
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình y = 3x - 2 :

Cho x = 0 ⇒y = - 2 ta được A(0; -2).

Cho y = 0 $\Rightarrow x = \dfrac{2}{3}$ ta được $B {\left(\dfrac{2}{3}; 0 \right)}.$

Biểu diễn cặp điểm A(0; -2) và $B{\left(\dfrac{2}{3}; 0 \right)}$ trên hệ trục tọa độ và đường thẳng AB chính là tập nghiệm của phương trình 3x - y = 2.

x + 5y = 3

1) Tìm nghiệm tổng quát của phương trình:

+) Nếu a ≠ 0 thì tìm x theo y. Khi đó công thức nghiệm là:

$\left\{ \matrix{ x = \dfrac{c - by}{a} \hfill \cr y \in \mathbb{R} \hfill \cr} \right.$

+) Nếu b ≠ 0 thì tìm y theo x. Khi đó công thức nghiệm là:

$\left\{ \matrix{ y = \dfrac{c - ax}{b} \hfill \cr x \in \mathbb{R} \hfill \cr} \right.$

2) Cách vẽ đường thẳng có phuương trình: ax+by=c.

+) Nếu a ≠ 0,\ b ≠ 0 thì vẽ đường thẳng $y=\dfrac{-a}{b}x+\dfrac{c}{b}$

+) Nếu a ≠ 0,\ b=0 thì vẽ đường thẳng $x=\dfrac{c}{a}$ song song hoặc trùng với trục tung.

+) Nếu a =0,\ b ≠ 0 thì vẽ đường thẳng $y=\dfrac{c}{a}$ song song hoặc trùng với trục hoành.

Ta có phương trình x + 5y = 3 $\Leftrightarrow x=-5y+3$ . Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x = -5y + 3 & & \\ y \in R & & \end{matrix}\right.$

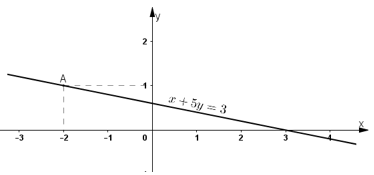
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình x=-5y+3 :

+) Cho x = 0 $\Rightarrow y = \dfrac{3}{5}$ ta được $C {\left( 0; \dfrac{3}{5} \right)}.$

+) Cho y = 0 ⇒ x = 3 ta được $D\left( {3;0} \right).$

Biểu diễn cặp điểm $C {\left( 0; \dfrac{3}{5} \right)}, D\left( {3;0} \right)$ trên hệ trục toa độ và đường thẳng CD chính là tập nghiệm của phương trình.

c) 4x - 3y = -1

Ta có phương trình 4x - 3y = -1 ↔ $3y=4x+1 \Leftrightarrow y=\dfrac{4}{3}x+\dfrac{1}{3}.$ Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x \in R & & \\ y = \dfrac{4}{3}x + \dfrac{1}{3}& & \end{matrix}\right.$

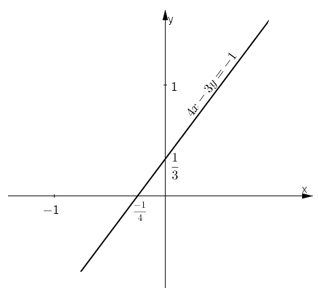
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình 4x-3y=-1

+) Cho $x = 0 \Rightarrow y = \dfrac{1}{3}$ ta được $A {\left(0;\dfrac{1}{3} \right)}$

+) Cho $y = 0 \Rightarrow x = -\dfrac{1}{4}$ ta được $B {\left(-\dfrac{1}{4};0 \right)}$

Biểu diễn cặp điểm $A {\left(0; \dfrac{1}{3} \right)}$ và $B {\left(-\dfrac{1}{4}; 0 \right)}$ trên hệ tọa độ và đường thẳng AB chính là tập nghiệm của phương trình 4x-3y=-1.

d) x +5y = 0

Ta có phương trình $x + 5y = 0 \Leftrightarrow x=-5y.$ Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x = -5y & & \\ y \in R & & \end{matrix}\right.$

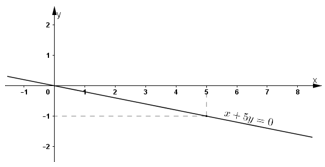
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình x+5y=0

+) Cho x = 0⇒ y = 0 ta được $O\left( {0;0} \right)$

+) Cho y = 1 ⇒ x = -5 ta được $A\left( {-5;1}\right).$

Biểu diễn cặp điểm O (0; 0) và A (-5; 1) trên hệ tọa độ và đường thẳng OA chính là tập nghiệm của phương trình x+5y=0.

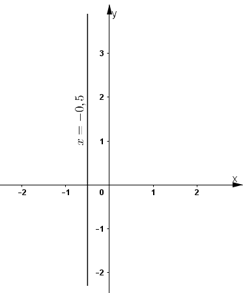
e) 4x + 0y = -2

Ta có phương trình $4x + 0y = -2 \Leftrightarrow 4x=-2 \Leftrightarrow x=\dfrac{-1}{2}$ . Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x = -\dfrac{1}{2} & & \\ y \in R & & \end{matrix}\right.$

Tập nghiệm là đường thẳng $x = -\dfrac{1}{2}$ đi qua $A {\left(-\dfrac{1}{2}; 0 \right)}$ và song song với trục tung.

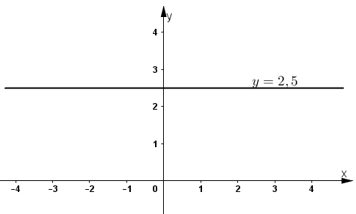
f) 0x + 2y = 5

$0x + 2y = 5 \Leftrightarrow 2y=5 \Leftrightarrow y=\dfrac{5}{2}$ . Nghiệm tổng quát của phương trình là:

$\left\{\begin{matrix} x \in R & & \\ y = \dfrac{5}{2} & & \end{matrix}\right.$

Tập nghiệm là đường thẳng $y = \dfrac{5}{2}$ đi qua $A {\left( 0;\dfrac{5}{2} \right)}$ và song song với trục hoành.

Bài 3 (trang 7 SGK Toán 9 Tập 2)

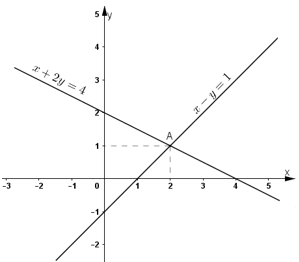
Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.

Xem gợi ý đáp án

Vẽ hình:

- Vẽ đường thẳng x + 2y = 4.

+ Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).

+ Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).

Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).

- Vẽ đường thẳng x – y = 1

+ Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).

+ Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).

Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).

- Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).

- Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.

Lý thuyết Bài 1: Phương trình bậc nhất hai ẩn

1. Khái niệm

Phương trình bậc nhất hai ẩn x, y là hệ thức dạng: ax + by = c (1)

Trong đó a, b và c là các số đã biết (a ≠ b hoặc b≠ 0 ).

2. Tập hợp nghiệm của phương trình

a) Một nghiệm của phương trình (1) là một cặp số

(x₀, y₀) sao cho ax₀+ by₀ = c.

b) Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm. Tập nghiệm của nó được biểu diễn bởi đường thẳng ax + by = c, kí hiệu là (d).

- Nếu a ≠ 0 và b ≠ 0 thì công thức nghiệm là:

$\left\{\begin{matrix} x \in R & & \\ y = \dfrac{c - ax}{b} & & \end{matrix}\right.$ hoặc $\left\{\begin{matrix} x = \dfrac{c - by}{a} & & \\ y \in R & & \end{matrix}\right.$