Giải Toán 9 trang 15, 16 - SGK Toán 9 Tập 2

Giải Toán lớp 9 trang 15, 16 tập 2 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và bài tập trong SGK bài 3 Giải hệ phương trình bằng phương pháp thế.

Giải Toán 9 Bài 3 trang 15, 16 tập 2 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 15, 16 tập 2 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Giải Toán 9 Bài 3: Giải hệ phương trình bằng phương pháp thế

Trả lời câu hỏi Toán 9 Bài 3
- Câu hỏi 1
- Câu hỏi 2
Giải Toán 9 trang 15 tập 2
Giải bài tập toán 9 trang 15 tập 2: Luyện tập
Lý thuyết Giải hệ phương trình bằng phương pháp thế

Trả lời câu hỏi Toán 9 Bài 3

Câu hỏi 1

Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ)

$\left\{ \begin{matrix} 4x-5y=3 \\ 3x-y=16 \\ \end{matrix} \right.$

Gợi ý đáp án

Ta biểu diễn y theo x từ phương trình thứ hai ta có:

$\left\{ \begin{matrix} 4x-5y=3 \\ 3x-y=16 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} 4x-5y=3 \\ y=3x-16 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} 4x-5.\left( 3x-16 \right)=3 \\ y=3x-16 \\ \end{matrix} \right.$

$\Leftrightarrow \left\{ \begin{matrix} -11x+80=3 \\ y=3x-16 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x=7 \\ y=5 \\ \end{matrix} \right.$

Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7; 5)

Câu hỏi 2

Bằng minh họa hình học và bằng phương pháp thế, chứng tỏ rằng hệ (IV) vô số nghiệm.

$\left( III \right)\left\{ \begin{matrix} 4x-2y=-6 \\ -2x+y=3 \\ \end{matrix} \right.$

Gợi ý đáp án

Minh họa hình học

$\left( III \right)\left\{ \begin{matrix} 4x-2y=-6 \\ -2x+y=3 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} 2y=4x+6\text{ (d)} \\ y=2x+3\text{ (d }\!\!'\!\!\text{ )} \\ \end{matrix} \right.$

Biểu diễn hai đường thẳng d và d’ như hình vẽ sau:

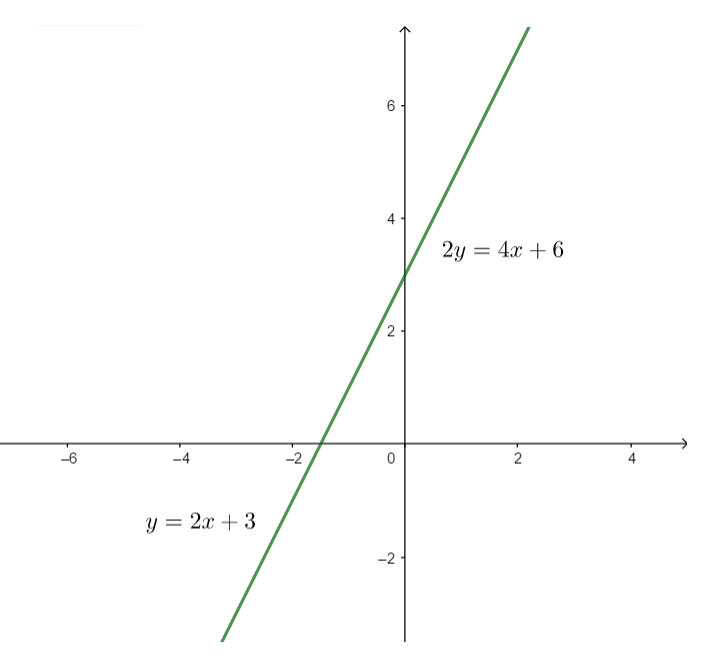
Nhận xét: Hai đường thẳng trên trùng nhau hay hệ phương trình (III) vô số nghiệm.

Giải Toán 9 trang 15 tập 2

Bài 12 (trang 15 SGK Toán 9 Tập 2)

Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{matrix} x - y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.$

b) $\left\{\begin{matrix} 7x - 3y =5 & & \\ 4x+y=2 & & \end{matrix}\right.$

c) $\left\{\begin{matrix} x +3y =-2 & & \\ 5x-4y=11 & & \end{matrix}\right.$

Xem gợi ý đáp án

a) $\left\{\begin{matrix} x - y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.$

Rút x từ phương trình trên rồi thế vào phương trình dưới , ta được:

$\left\{ \matrix{ x - y = 3 \hfill \cr 3x - 4y = 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = 3 + y \hfill \cr 3\left( {3 + y} \right) - 4y = 2 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = 3 + y \hfill \cr 9 + 3y - 4y = 2 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = 3 + y \hfill \cr - y = 2 - 9 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = 3 + y \hfill \cr y = 7 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = 3 + 7 \hfill \cr y = 7 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = 10 \hfill \cr y = 7 \hfill \cr} \right.$

Vậy hệ đã cho có nghiệm là (x;y)=(10; 7).

b) $\left\{\begin{matrix} 7x - 3y =5 & & \\ 4x+y=2 & & \end{matrix}\right.$

Rút y từ phương trình dưới rồi thế vào phương trình trên, ta có:

$\left\{ \begin{array}{l}7x - 3y = 5\\4x + y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x - 3y = 5\\y = 2 - 4x\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x - 3.\left( {2 - 4x} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x - 6 + 12x = 5\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\7x + 12x = 5 + 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\19x = 11\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = 2 - 4x\\x = \dfrac{{11}}{{19}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{{19}}\\y = 2 - 4.\dfrac{{11}}{{19}}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{{19}}\\y = - \dfrac{6}{{19}}\end{array} \right.$

Vậy hệ có nghiệm duy nhất là ${\left(\dfrac{11}{19}; \dfrac{-6}{19} \right)}$

c) $\left\{\begin{matrix} x +3y =-2 & & \\ 5x-4y=11 & & \end{matrix}\right.$

Rút x từ phương trình trên rồi thế vào phương trình dưới, ta có:

$\left\{ \matrix{ x + 3y = - 2 \hfill \cr 5x - 4y = 11 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 2 - 3y \hfill \cr 5\left( { - 2 - 3y} \right) - 4y = 11 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - 2 - 3y \hfill \cr - 10 - 15y - 4y = 11 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - 2 - 3y \hfill \cr - 15y - 4y = 11 + 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 2 - 3y \hfill \cr - 19y = 21 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - 2 - 3y \hfill \cr y = - \dfrac{ 21}{ 19} \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - 2 - 3. \dfrac{ - 21}{19} \hfill \cr y = - \dfrac{21}{19} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = \dfrac{25}{19} \hfill \cr y = - \dfrac{21}{19} \hfill \cr} \right.$

Vậy hệ có nghiệm duy nhất là ${\left(\dfrac{25}{19}; \dfrac{-21}{19} \right)}$

Bài 13 (trang 15 SGK Toán 9 Tập 2)

Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{matrix} 3x - 2y = 11 & & \\ 4x - 5y = 3& & \end{matrix}\right.;$

b) $\left\{\begin{matrix} \dfrac{x}{2}- \dfrac{y}{3} = 1& & \\ 5x - 8y = 3& & \end{matrix}\right.$

Xem gợi ý đáp án

a) Ta có:

$\left\{ \matrix{ 3x - 2y = 11 \hfill \cr 4x - 5y = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 2y = 3x - 11 \hfill \cr 4x - 5y = 3 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ y = \dfrac{3x - 11}{2}\ (1) \hfill \cr 4x - 5.\dfrac{3x - 11}{ 2} = 3 \ (2) \hfill \cr} \right.$

Giải phương trình (2):

$4x - 5.\dfrac{3x - 11}{ 2} = 3 \Leftrightarrow 4x - \dfrac{15x - 55}{ 2} = 3$

$\Leftrightarrow \dfrac{4x.2}{2} - \dfrac{15x - 55}{ 2} = \dfrac{3.2}{2} \Leftrightarrow \dfrac{8x}{2} - \dfrac{15x - 55}{2} = \dfrac{6}{2}$

$\Leftrightarrow \dfrac{8x - 15x + 55}{2} = \dfrac{6}{2} \Leftrightarrow 8x - 15x + 55 = 6 \Leftrightarrow - 7x = 6 - 55$

$\Leftrightarrow - 7x = - 49 \Leftrightarrow x=7$

Thay x=7 vào phương trình (1), ta được:

$y = \dfrac{3.7 - 11}{2}=5$

Vậy hệ có nghiệm duy nhất là (7; 5).

b) Ta có:

$\left\{ \matrix{ \dfrac{x}{2} - \dfrac{y}{3} = 1 \hfill \cr 5x - 8y = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ \dfrac{x }{2} = 1 + \dfrac{y}{3} \hfill \cr 5x - 8y = 3 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = 2 + \dfrac{2y}{3} \ (1) \hfill \cr 5{\left(2 + \dfrac{2y}{3} \right)} - 8y = 3 \ (2) \hfill \cr} \right.$

Giải phương trình (2), ta được:

$5{\left(2 + \dfrac{2y}{3} \right)} - 8y = 3 \Leftrightarrow 5.2 + 5. \dfrac{2y}{3}-8y = 3 \Leftrightarrow 10 + \dfrac{10y}{3} -8y =3$

$\Leftrightarrow \dfrac{30}{3} +\dfrac{10y}{3} - \dfrac{24y}{3} = \dfrac{9}{3} \Leftrightarrow 30+ 10y -24y=9$

$\Leftrightarrow -14y=9-30 \Leftrightarrow -14y=-21$

$\Leftrightarrow y=\dfrac{21}{14} \Leftrightarrow y= \dfrac{3}{2}$

Thay $y= \dfrac{3}{2}$ vào (1), ta được:

$x = 2 + \dfrac{2. \dfrac{3}{2}}{3}=2+\dfrac{3}{3}=3.$

Vậy hệ phương trình có nghiệm duy nhất ${\left(3; \dfrac{3}{2} \right)}.$

Bài 14 (trang 15 SGK Toán 9 Tập 2)

Giải các hệ phương trình bằng phương pháp thế:

a) $\left\{\begin{matrix} x + y\sqrt{5} = 0& & \\ x\sqrt{5} + 3y = 1 - \sqrt{5}& & \end{matrix}\right.$

b) $\left\{\begin{matrix} (2 - \sqrt{3})x - 3y = 2 + 5\sqrt{3}& & \\ 4x + y = 4 -2\sqrt{3}& & \end{matrix}\right.$

Xem gợi ý đáp án

a) Ta có:

$\left\{ \matrix{ x + y\sqrt 5 = 0 \hfill \cr x\sqrt 5 + 3y = 1 - \sqrt 5 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - y\sqrt 5 \hfill \cr \left( { - y\sqrt 5 } \right).\sqrt 5 + 3y = 1 - \sqrt 5 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - y\sqrt 5 \hfill \cr - 5y + 3y = 1 - \sqrt 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - y\sqrt 5 \hfill \cr - 2y = 1 - \sqrt 5 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - y\sqrt 5 \hfill \cr y = \dfrac{1 - \sqrt 5 }{ - 2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - y\sqrt 5 \hfill \cr y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - \dfrac{\sqrt 5 - 1}{ 2}.\sqrt 5 \hfill \cr y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - \dfrac{5 - \sqrt 5 }{2} \hfill \cr y = \dfrac{\sqrt 5 - 1}{2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = \dfrac{\sqrt 5 - 5}{ 2} \hfill \cr y = \dfrac{\sqrt 5 - 1}{ 2} \hfill \cr} \right.$

Vậy hệ phương trình có nghiệm duy nhất ${\left(\dfrac{\sqrt 5 - 5}{ 2} ; \dfrac{\sqrt 5 - 1}{ 2} \right)}$

b) $\left\{\begin{matrix} (2 - \sqrt{3})x - 3y = 2 + 5\sqrt{3}& & \\ 4x + y = 4 -2\sqrt{3}& & \end{matrix}\right.$

Ta có:

$\left\{ \matrix{ \left( {2 - \sqrt 3 } \right)x - 3y = 2 + 5\sqrt 3 \hfill \cr 4x + y = 4 - 2\sqrt 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ \left( {2 - \sqrt 3 } \right)x - 3\left( {4 - 2\sqrt 3 - 4x} \right) = 2 + 5\sqrt 3 \ (1) \hfill \cr y = 4 - 2\sqrt 3 - 4x \ (2) \hfill \cr} \right.$

Giải phương trình (1), ta được:

$( 2 - \sqrt 3 )x - 3(4 - 2\sqrt 3 - 4x) = 2 + 5\sqrt 3 \Leftrightarrow 2x -\sqrt 3 x -12 + 6 \sqrt 3 + 12x=2+ 5 \sqrt 3$

$\Leftrightarrow 2x -\sqrt 3 x + 12x=2+ 5 \sqrt 3 +12 -6 \sqrt 3 \Leftrightarrow (2 -\sqrt 3 + 12)x= 2+12 +5\sqrt 3 -6 \sqrt 3$

$\Leftrightarrow (14- \sqrt 3)x=14-\sqrt 3 \Leftrightarrow x=1$

Thay x=1, vào (2), ta được:

$y = 4 - 2\sqrt 3 - 4.1=-2 \sqrt 3.$

Vậy hệ phương trình có nghiệm duy nhất $(1; -2 \sqrt 3).$

Giải bài tập toán 9 trang 15 tập 2: Luyện tập

Bài 15 (trang 15 SGK Toán 9 Tập 2)

Giải hệ phương trình $\left\{\begin{matrix} x + 3y = 1 & & \\ (a^{2} + 1)x + 6y = 2a & & \end{matrix}\right.$ trong mỗi trường hợp sau:

a) a = -1

b) a = 0

c) a = 1

Xem gợi ý đáp án

a) a = -1

Thay a = -1 vào hệ, ta được:

$\left\{\begin{matrix} x + 3y = 1 & & \\ {\left((-1)^2+1 \right)}x+ 6y = 2.(-1) & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x + 3y = 1 & & \\ 2x+ 6y = -2 & & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} x + 3y = 1 & & \\ x+ 3y = -1 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x = 1 -3y & & \\ (1-3y)+ 3y = -1 & & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} x = 1 -3y & & \\ 1 = -1 (vô \ lý )& & \end{matrix}\right.$

Vậy hệ phương trình trên vô nghiệm.

b) a = 0

Thay a = 0 vào hệ, ta được:

$\left\{ \matrix{ x + 3y = 1 \hfill \cr \left( {0 + 1} \right)x + 6y = 2.0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x + 3y = 1 \hfill \cr x + 6y = 0 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x + 3y = 1 \hfill \cr x = - 6y \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ - 6y + 3y = 1 \hfill \cr x = - 6y \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ - 3y = 1 \hfill \cr x = - 6y \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ y = \dfrac{ - 1}{3} \hfill \cr x = - 6y \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ y = \dfrac{ - 1}{3} \hfill \cr x = - 6. \dfrac{ - 1}{3} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ y = \dfrac{ - 1}{3} \hfill \cr x = 2 \hfill \cr} \right.$

Hệ phương trình có nghiệm ${\left(2; -\dfrac{1}{3} \right)} .$

c) a = 1

Thay a = 1 vào hệ, ta được:

$\left\{ \matrix{ x + 3y = 1 \hfill \cr ({1^2} + 1)x + 6y = 2.1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x + 3y = 1 \hfill \cr 2x + 6y = 2 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x + 3y = 1 \hfill \cr x + 3y = 1 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 1 - 3y\\1 - 3y + 3y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1 - 3y\\1 = 1\left( {luôn\,đúng} \right)\end{array} \right.$

Vậy hệ phương trình có vô số nghiệm $\left\{ \begin{array}{l}x = 1 - 3y\\y \in \mathbb{R}\end{array} \right.$

Bài 16 (trang 16 SGK Toán 9 Tập 2)

Giải các hệ phương trình sau bằng phương pháp thế

a) $\left\{\begin{matrix} 3x - y = 5 & & \\ 5x + 2y = 23 & & \end{matrix}\right.$

b) $\left\{\begin{matrix} 3x +5y = 1 & & \\ 2x -y =-8 & & \end{matrix}\right.$

$c. \left\{\begin{matrix} \dfrac{x}{y} = \dfrac{2}{3}& & \\ x + y - 10 = 0 & & \end{matrix}\right.$

Xem gợi ý đáp án

a) Ta có:

$\left\{ \matrix{ 3x - y = 5 \hfill \cr 5x + 2y = 23 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ y = 3x - 5 \hfill \cr 5x + 2\left( {3x - 5} \right) = 23 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ y = 3x - 5 \hfill \cr 5x + 6x - 10 = 23 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ y = 3x - 5 \hfill \cr 11x = 23 + 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ y = 3x - 5 \hfill \cr 11x = 33 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ y = 3x - 5 \hfill \cr x = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ y = 3.3 - 5 \hfill \cr x = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ y = 4 \hfill \cr x = 3 \hfill \cr} \right.$

Vậy hệ có nghiệm duy nhất là (x; y) = (3; 4).

b) Ta có:

$\left\{ \matrix{ 3x + 5y = 1 \hfill \cr 2x - y = - 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 3x + 5y = 1 \hfill \cr y = 2x + 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 3x + 5\left( {2x + 8} \right) = 1 \hfill \cr y = 2x + 8 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ 3x + 10x + 40 = 1 \hfill \cr y = 2x + 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 13x = 1 - 40 \hfill \cr y = 2x + 8 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ 13x = - 39 \hfill \cr y = 2x + 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 3 \hfill \cr y = 2x + 8 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = - 3 \hfill \cr y = 2.\left( { - 3} \right) + 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 3 \hfill \cr y = 2 \hfill \cr} \right.$

Vậy hệ có nghiệm (x; y) = (-3; 2).

c) Ta có:

$\left\{ \matrix{ \dfrac{x}{y} = \dfrac{2}{3} \hfill \cr x + y - 10 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = \dfrac{2y}{3} \hfill \cr \dfrac{2y}{3} + y = 10 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = \dfrac{2y}{3} \hfill \cr {\left( \dfrac{2}{3} + 1 \right)}y = 10 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = \dfrac{2y}{3} \hfill \cr \dfrac{5}{ 3}y = 10 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = \dfrac{2y}{3} \hfill \cr y = 6 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = \dfrac{2.6}{3} \hfill \cr y = 6 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = 4 \hfill \cr y = 6 \hfill \cr} \right.$

Vậy nghiệm của hệ là (x; y) = (4; 6).

Bài 17 (trang 16 SGK Toán 9 Tập 2)

$a) \left\{\begin{matrix} x\sqrt{2}- y \sqrt{3}=1 & & \\ x + y\sqrt{3} = \sqrt{2}& & \end{matrix}\right.$

$b) \left\{\begin{matrix} x - 2\sqrt{2} y = \sqrt{5}& & \\ x\sqrt{2} + y = 1 - \sqrt{10}& & \end{matrix}\right.$

$c. \left\{\begin{matrix} (\sqrt{2}- 1)x - y = \sqrt{2}& & \\ x + (\sqrt{2}+ 1)y = 1& & \end{matrix}\right.$

Xem gợi ý đáp án

a) Ta có:

$\left\{ \matrix{ x\sqrt 2 - y\sqrt 3 = 1 \hfill \cr x + y\sqrt 3 = \sqrt 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x\sqrt 2 - y\sqrt 3 = 1 \hfill \cr x = \sqrt 2 - y\sqrt 3 \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ \left( {\sqrt 2-y\sqrt 3 } \right)\sqrt 2 - y\sqrt 3 = 1 \ (1) \hfill \cr x = \sqrt 2 - y\sqrt 3 \ (2) \hfill \cr} \right.$

Giải phương trình (1), ta được:

$( \sqrt 2 - y\sqrt 3)\sqrt 2 - y\sqrt 3 = 1 \Leftrightarrow (\sqrt 2)^2 - y\sqrt 3 . \sqrt 2 - y\sqrt 3 = 1$

$\Leftrightarrow 2 - y\sqrt 3 . \sqrt 2 - y\sqrt 3 = 1 \Leftrightarrow -y\sqrt 3. \sqrt 2 - y\sqrt 3 = 1 - 2$

$\begin{array}{l} \Leftrightarrow - y\sqrt 6 - y\sqrt 3 = - 1\\ \Leftrightarrow y\left( {\sqrt 6 + \sqrt 3 } \right) = 1\\ \Leftrightarrow y = \dfrac{1}{{\sqrt 6 + \sqrt 3 }}\\ \Leftrightarrow y = \dfrac{{\sqrt 6 - \sqrt 3 }}{3}\\ \Leftrightarrow y = \dfrac{{\sqrt 3 \left( {\sqrt 2 - 1} \right)}}{3} \end{array}$

Thay y tìm được vào phương trình (2), ta được:

$x = \sqrt 2 - \dfrac{\sqrt 3 (\sqrt 2 -1)}{3}.\sqrt 3$

$\Leftrightarrow x=\sqrt 2 - \dfrac{\sqrt 3 .\sqrt 3(\sqrt 2 -1)}{3} \Leftrightarrow x=\sqrt 2 - \dfrac{ 3(\sqrt 2 -1)}{3} =\sqrt 2 - (\sqrt 2 -1)$

$\Leftrightarrow x=\sqrt 2 -\sqrt 2 +1=1\\$

Vậy hệ phương trình đã cho có nghiệm duy nhất là: ${\left( 1;\dfrac{\sqrt 3 (\sqrt 2 -1)}{3} \right)}$

b) Ta có:

$\left\{ \matrix{ x - 2\sqrt 2 y = \sqrt 5 \hfill \cr x\sqrt 2 + y = 1 - \sqrt {10} \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ x = 2\sqrt 2 y + \sqrt 5 \ (1) \hfill \cr \left( {2\sqrt 2 y + \sqrt 5 } \right).\sqrt 2 + y = 1 - \sqrt {10}\ (2) \hfill \cr} \right.$

Giải phương trình (2), ta được:

$\left( {2\sqrt 2 y + \sqrt 5 } \right).\sqrt 2 + y = 1 - \sqrt {10} \Leftrightarrow 2(\sqrt 2 .\sqrt 2)y + \sqrt 5 .\sqrt 2 + y = 1 - \sqrt {10}$

$\Leftrightarrow 4y + \sqrt{10}+y=1- \sqrt{10} \Leftrightarrow 4y +y=1- \sqrt{10}- \sqrt{10}$

$\Leftrightarrow 5y=1-2 \sqrt{10} \Leftrightarrow y=\dfrac{1-2 \sqrt{10}}{5}$

Thay $y=\dfrac{1-2 \sqrt{10}}{5}$ vào (1), ta được:

$x = 2\sqrt 2 .\dfrac{1-2 \sqrt{10}}{5} + \sqrt 5= \dfrac{2\sqrt 2 -4 \sqrt{20}}{5} + \sqrt 5$

$\Leftrightarrow x=\dfrac{2\sqrt 2 -4 .2\sqrt{5}}{5} + \sqrt 5=\dfrac{2\sqrt 2 -8\sqrt{5}+ 5\sqrt 5}{5}$

$\Leftrightarrow x=\dfrac{2 \sqrt 2 -3 \sqrt 5}{5}$

Vậy hệ có nghiệm duy nhất là: $(x; y) = {\left(\dfrac{2\sqrt{2} - 3\sqrt{5}}{5};\dfrac{1 - 2\sqrt{10}}{5}\right)}$

c) Ta có:

$\left\{ \matrix{ \left( {\sqrt 2 - 1} \right)x - y = \sqrt 2 \hfill \cr x + \left( {\sqrt 2 + 1} \right)y = 1 \hfill \cr} \right.$

$\left\{ \begin{array}{l}y = \left( {\sqrt 2 - 1} \right)x - \sqrt 2 \,\,\,\,\,\left( 1 \right)\\x + \left( {\sqrt 2 + 1} \right)\left[ {\left( {\sqrt 2 - 1} \right)x - \sqrt 2 } \right] = 1\,\,\,\left( 2 \right)\end{array} \right.$

Giải phương trình (2), ta được:

$x + \left( {\sqrt 2 + 1} \right)\left[ { \left( {\sqrt 2 - 1} \right)x} -\sqrt 2 \right] = 1$

$\Leftrightarrow x + (\sqrt 2 + 1) (\sqrt 2 - 1)x -( \sqrt 2 + 1). \sqrt 2 = 1$

$\Leftrightarrow x + {\left((\sqrt 2)^2 - 1^2 \right)}x-( 2 + \sqrt 2) = 1$

$\Leftrightarrow x + x = 1+( 2 + \sqrt 2) \Leftrightarrow 2x =3 +\sqrt 2 \Leftrightarrow x=\dfrac{3+ \sqrt 2}{2}$

Thay $x=\dfrac{3+ \sqrt 2}{2}$ vào (1), ta được:

$y = \left( {\sqrt 2 - 1} \right).\dfrac{3+ \sqrt 2}{2} - \sqrt 2$

$\Leftrightarrow y= \dfrac{(\sqrt 2 - 1 )(3+ \sqrt 2)}{2} - \sqrt 2 \Leftrightarrow y= \dfrac{3\sqrt 2 -3 +2 -\sqrt 2}{2} - \sqrt 2$

$\Leftrightarrow y= \dfrac{2\sqrt 2 -1}{2} - \sqrt 2 \Leftrightarrow y= \dfrac{2\sqrt 2 -1-2\sqrt 2}{2} \Leftrightarrow y= \dfrac{-1}{2}$

Vậy hệ có nghiệm $(x; y) = {\left(\dfrac{3 + \sqrt{2}}{2};\dfrac{-1}{2} \right)}$

Bài 18 (trang 16 SGK Toán 9 Tập 2)

a) Xác định các hệ số a và b, biết rằng hệ phương trình

$\left\{\begin{matrix} 2x + by=-4 & & \\ bx - ay=-5& & \end{matrix}\right.$

có nghiệm là (1; -2)

b) Cũng hỏi như vậy, nếu hệ phương trình có nghiệm là $(\sqrt{2} - 1; \sqrt{2}).$

Xem gợi ý đáp án

a) Hệ phương trình có nghiệm là (1; -2) khi và chỉ khi (1; -2) thỏa mãn hệ phương trình. Thay x=1, y=-2 vào hệ, ta có:

$\left\{\begin{matrix} 2 - 2b=-4 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2b=6 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ b+2a=-5 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 3+2a=-5 & & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 2a = -5 - 3& & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b=3 & & \\ 2a = -8& & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} b=3 & & \\ a = -4 & & \end{matrix}\right.$

Vậy a=-4, b=3 thì hệ có nghiệm là (1; -2).

b) Thay $x=\sqrt 2 - 1;\ y= \sqrt 2$ vào hệ phương trình đã cho, ta có:

$\left\{\begin{matrix} 2(\sqrt{2}-1)+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2\sqrt{2}-2+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} 2\sqrt{2}-2+b\sqrt{2}= -4 & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b\sqrt{2}= -2 - 2\sqrt{2} & & \\ (\sqrt{2}-1)b - a\sqrt{2}= -5& & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} b= -(2 + \sqrt{2}) & & \\ a\sqrt{2}= -(2 + \sqrt{2})(\sqrt{2}-1)+5& & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b= -(2 + \sqrt{2}) & & \\ a\sqrt{2}= -\sqrt{2}+5& & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} a = \dfrac{-2+5\sqrt{2}}{2} & & \\ b = -(2+ \sqrt{2})& & \end{matrix}\right.$

Vậy $a = \dfrac{-2+5\sqrt{2}}{2},\ b=-(2+ \sqrt{2})$ thì hệ trên có nghiệm là $(\sqrt 2 -1; \sqrt 2).$

Bài 19 (trang 16 SGK Toán 9 Tập 2)

Biết rằng: Đa thức P(x) chia hết cho đa thức x - a khi và chỉ khi P(a) = 0.

Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x - 3:

$P(x) = m{x^3} + (m - 2){x^2} - (3n - 5)x - 4n$

Xem gợi ý đáp án

+) Ta có: P(x) chia hết cho $x + 1 \Leftrightarrow P(-1)=0$

$\Leftrightarrow m.(-1)^3 + (m - 2).(-1)^2 - (3n - 5).(-1) - 4n=0$

$\Leftrightarrow -m + m - 2 + 3n - 5 - 4n = 0 \Leftrightarrow -n-7=0 \Leftrightarrow n+7=0 (1)$

+) Lại có: P(x) chia hết cho $x - 3 \Leftrightarrow P(3)=0$

$\Leftrightarrow m.3^3 + (m - 2).3^2 - (3n - 5).3 - 4n=0$

$\Leftrightarrow 27m + 9(m - 2) - 3(3n - 5) - 4n = 0$

$\Leftrightarrow 27m + 9m - 18 - 9n + 15 - 4n = 0$

$\Leftrightarrow 36m-13n=3 (2)$

Từ (1) và (2), ta có hệ phương trình ẩn m và n.

$\left\{\begin{matrix} n+7 = 0 & & \\ 36m - 13n = 3 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} n = -7 & & \\ 36m -13.(-7)= 3 & & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} n = -7 & & \\ 36m = -88 & & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} n = -7& & \\ m = \dfrac{-22}{9}& & \end{matrix}\right.$

Vậy $m=\dfrac{-22}{9},\ n=-7.$

Lý thuyết Giải hệ phương trình bằng phương pháp thế

1. Phương trình bậc nhất 2 ẩn

Phương trình bậc nhất hai ẩn x, y là hệ thức có dạng: ax + by = c, trong đó a, b, c là các số đã biết (trong đó a ≠ 0 hoặc b ≠ 0 ).

* Trong phương trình ax + by = c, nếu giá trị của vế trái tại x = x0 và y =y0 bằng vế phải thì cặp số (x0; y0) được gọi là một nghiệm của phương trình.

Chú ý: Trong mặt phẳng tọa độ Oxy mỗi nghiệm của phương trình ax + by = c được biểu diễn bởi một điểm. Nghiệm (x0; y0) được biểu diễn bởi điểm có tọa độ (x0; y0).

Ví dụ: Các phương trình bậc nhất hai ẩn là 2x + y = 1; x - y = 2; ....

2. Quy tắc thế

Qui tắc thế dùng để biến đổi một hệ phương trình thành hệ phương trình tương đương.

Quy tắc thế gồm hai bước sau:

Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thứ nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).

Bước 2: Dùng phương trình mới để thay thế cho phương trình thứ hai trong hệ (và giữ nguyên phương trình thứ nhất) ta được hệ mới tương đương với hệ phương trình đã cho.

3. Cách giải hệ phương trình bằng phương pháp thế

Căn cứ vào quy tắc thế, để giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế, ta làm như sau:

Bước 1. Rút x hoặc y từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.

Bước 2. Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.

3. Chú ý

+ Nếu thấy xuất hiện phương trình có các hệ số của hai ẩn đểu bằng 0 thì hệ phương trình đã cho có thể có vô số nghiệm hoặc vô nghiệm.

Giải Toán 9 trang 15, 16 - SGK Toán 9 Tập 2

Giải Toán 9 Bài 3: Giải hệ phương trình bằng phương pháp thế

Giải SGK Toán 9 Tập 2 (trang 15, 16)

Giải Toán 9 Bài 3: Giải hệ phương trình bằng phương pháp thế

Trả lời câu hỏi Toán 9 Bài 3

Câu hỏi 1

Câu hỏi 2

Giải Toán 9 trang 15 tập 2

Bài 12 (trang 15 SGK Toán 9 Tập 2)

Bài 13 (trang 15 SGK Toán 9 Tập 2)

Bài 14 (trang 15 SGK Toán 9 Tập 2)

Giải bài tập toán 9 trang 15 tập 2: Luyện tập

Bài 15 (trang 15 SGK Toán 9 Tập 2)

Bài 16 (trang 16 SGK Toán 9 Tập 2)

Bài 17 (trang 16 SGK Toán 9 Tập 2)

Bài 18 (trang 16 SGK Toán 9 Tập 2)

Bài 19 (trang 16 SGK Toán 9 Tập 2)

Lý thuyết Giải hệ phương trình bằng phương pháp thế

1. Phương trình bậc nhất 2 ẩn

2. Quy tắc thế

3. Cách giải hệ phương trình bằng phương pháp thế

Liên kết tải về

Chủ đề liên quan

Học tập

Lớp 9

Giải Toán 9

Chia sẻ

Có thể bạn quan tâm

Được tải nhiều nhất

Bài viết mới nhất