Toán 10 Cánh diều trang 77 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời câu hỏi phần khởi động và 7 bài tập trong SGK Toán 10 tập 1.
Giải Toán 10 bài 2 Cánh diều trang 77 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa. Giải Toán 10 Cánh diều trang 77 tập 1 là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác
Câu hỏi khởi động trang 72 Toán 10 Tập 1
Giải Toán 10 trang 77 Cánh diều - Tập 1
Câu hỏi khởi động trang 72 Toán 10 Tập 1
Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:
Từ vị trí A, đo góc nghiêng ![]() so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng
so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng ![]() so với bờ biển tới vị trí C đã chọn (Hình 18).
so với bờ biển tới vị trí C đã chọn (Hình 18).
Bằng cách giải tam giác ABC,họ tính được khoảng cách AC.
Giải tam giác được hiểu như thế nào?
Gợi ý đáp án
Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
![]()
Mà AB=d, ![]()
![]()
Giải Toán 10 trang 77 Cánh diều - Tập 1
Bài 1 trang 77
Cho tam giác ABC có BC = 12,CA = 15,![]() Tính:
Tính:
a) Độ dài cạnh AB.
b) Số đo các góc A, B.
c) Diện tích tam giác ABC.
Gợi ý đáp án
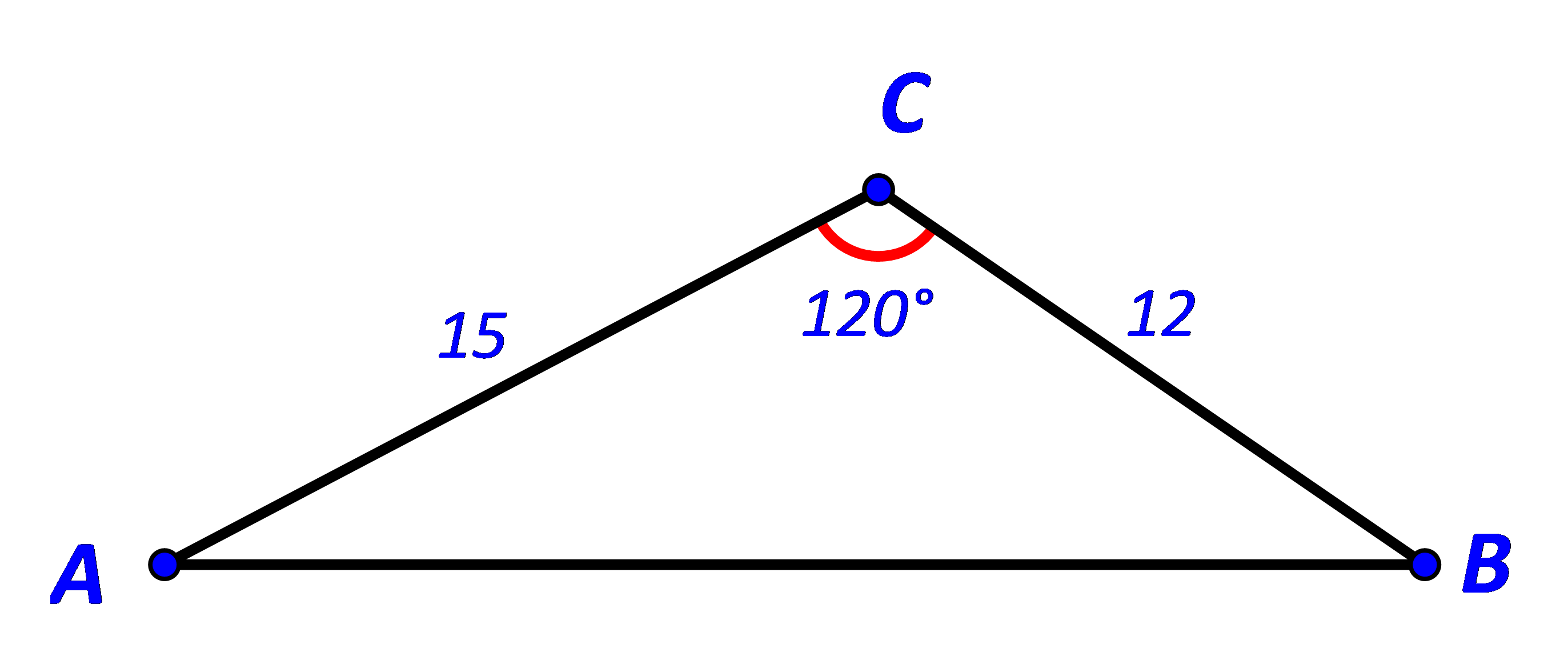
a) Áp dụng định lí cosin trong tam giác ABC ta có:
![]()

b) Áp dụng định lí sin trong tam giác ABC, ta có:
![]()
![]()
![]()
Khi đó:![]()
c)
Diện tích tam giác ABC là: ![]()
Bài 2 trang 77
Cho tam giác ABC có AB = 5,BC = 7,![]() . Tính độ dài cạnh AC.
. Tính độ dài cạnh AC.
Gợi ý đáp án
Áp dụng định lí sin trong tam giác ABC ta có:
![]()
![]()
![]()
Ta có: ![]()
Áp dụng định lí cosin trong tam giác ABC ta có:

Vậy độ dài cạnh AC là 3.
Bài 3 trang 77
Cho tam giác ABC có ![]() Tính:
Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
Gợi ý đáp án
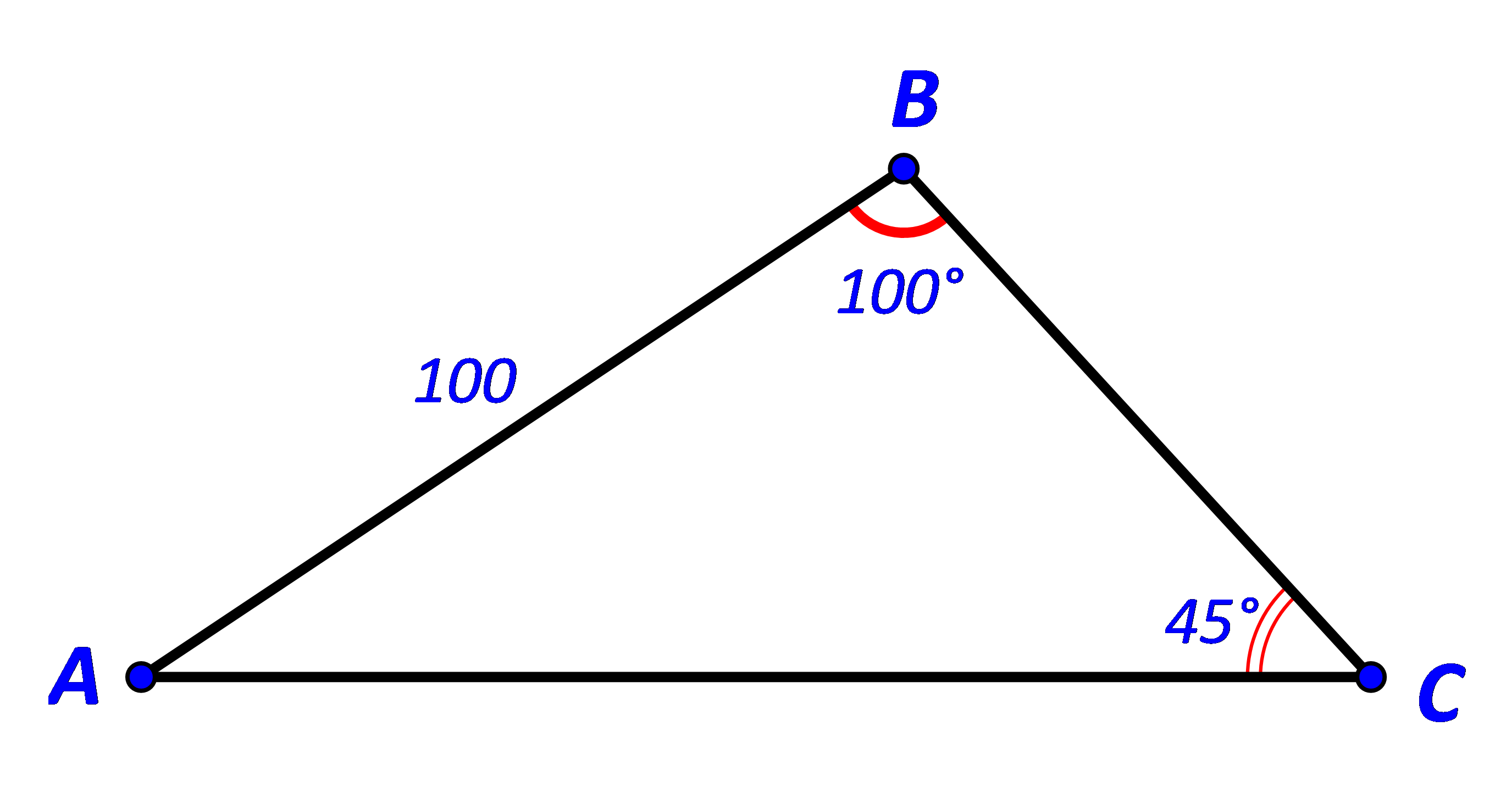
a)
Ta có: ![]()
Áp dụng định lí sin trong tam giác ABC ta có:
![]()

b)
Diện tích tam giác ABC là: ![]()
Bài 4 trang 77
Cho tam giác ABC có AB = 12,AC = 15,BC = 20. Tính:
a) Số đo các góc A, B, C.
b) Diện tích tam giác ABC.
Gợi ý đáp án
a) Áp dụng định lí cosin trong tam giác ABC, ta có:
![]()
Thay a = BC = 20;b = AC = 15;c = AB = 12.
![]()
![]()
![]()
b)
Diện tích tam giác ABC là: ![]()
Bài 5 trang 77
Tính độ dài cạnh AB trong mỗi trường hợp sau:
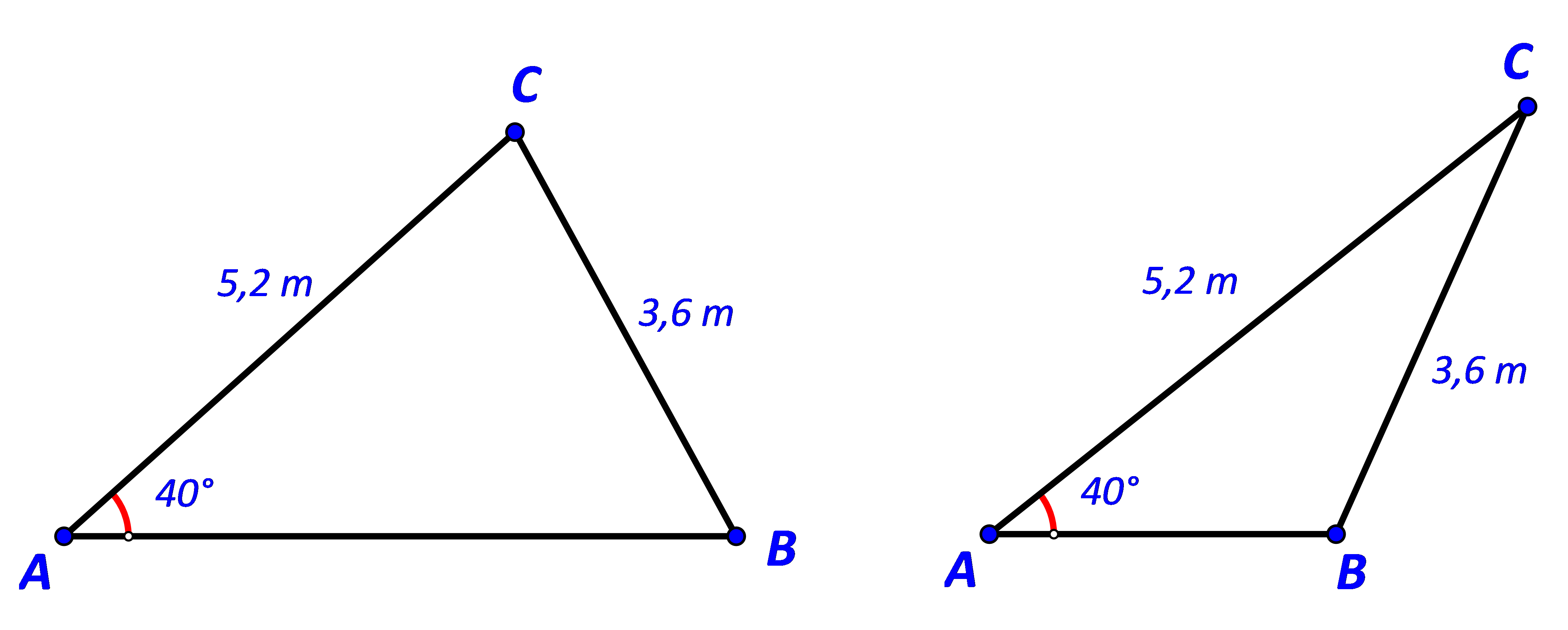
Gợi ý đáp án
Áp dụng định lí sin trong tam giác ABC, ta có:
![]()
![]()
![]()
Trường hợp 1![]()
Ta có:![]()
Áp dụng định lí sin trong tam giác ABC, ta có:
![]()
![]()
Trường hợp 2: ![]()
Ta có: ![]()
Áp dụng định lí sin trong tam giác ABC, ta có:
![]()
![]()
Vậy AB = 5,32 hoặc AB = 2,65.
Bài 6 trang 77
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và ![]() (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).
(Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).
Gợi ý đáp án
Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
![]()

Vậy khoảng cách AB là 1433,2 m.
Bài 7 trang 77
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là ![]() và
và ![]() Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Gợi ý đáp án
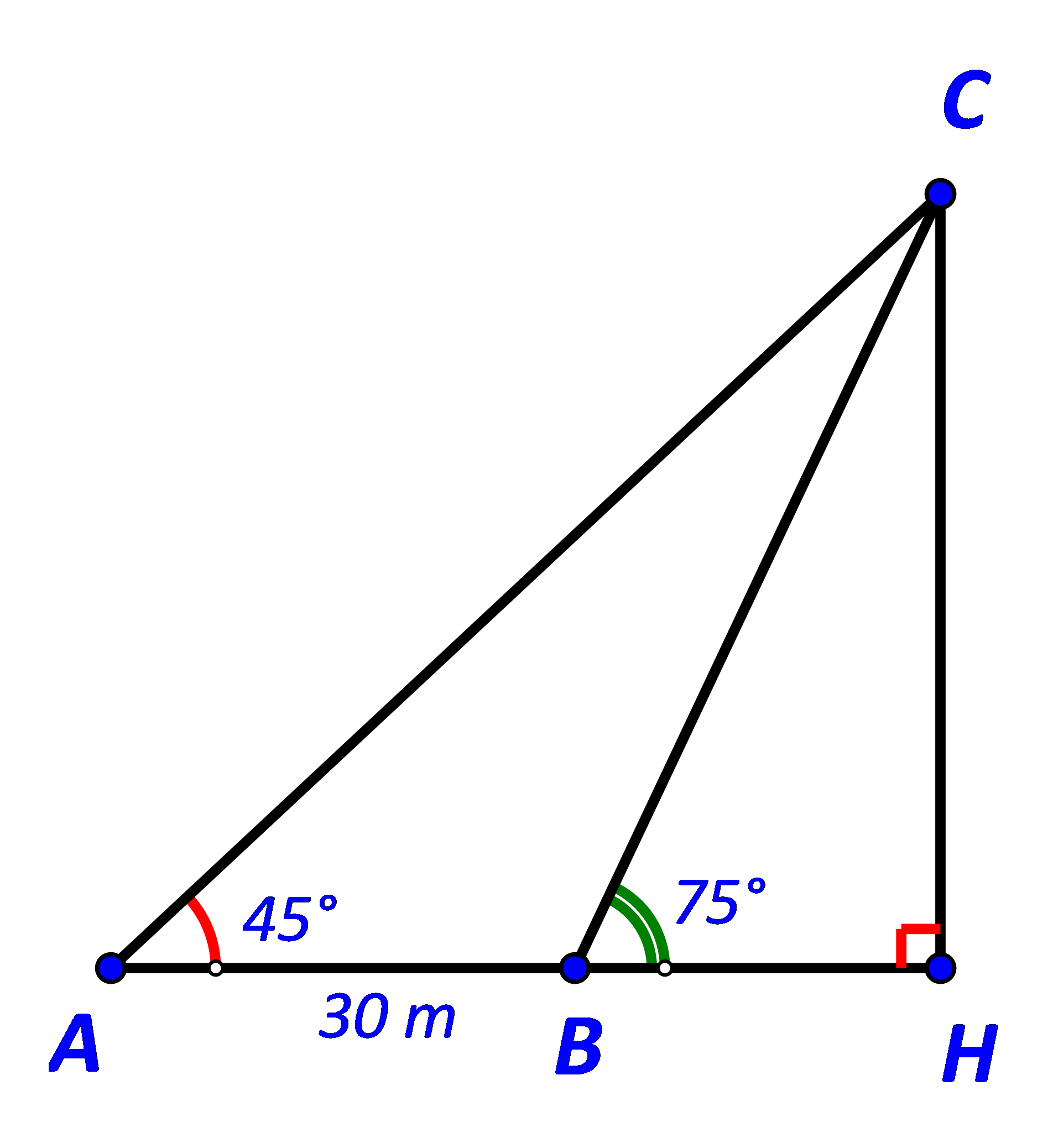
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
Ta có:![]()
![]()
Áp dụng định lí sin trong tam giác ABC ta có:
![]()
![]()
Tam giác ACH vuông tại H nên ta có:
![]()
Vậy ngọn hải đăng cách bờ biển 56 m.
