Giải Toán 10 Bài tập cuối chương III trang 60, 61 Cánh diều

Giải Toán 10 Bài tập cuối chương III giúp các em học sinh lớp 10 tham khảo, biết cách giải các bài tập trong SGK Toán 10 Tập 1 trang 60, 61 sách Cánh diều.

Giải SGK Toán 10 Bài tập cuối chương 3: Hàm số và đồ thị sách Cánh diều Tập 1 giúp các em học sinh nắm được cách trình bày, cách triển khai để giải được các bài tập từ bài 1 đến bài 6 trong sách giáo khoa. Từ đó các em học sinh tự bồi dưỡng và nâng cao kiến thức tự tin giải quyết tốt các bài tập. Đồng thời đây cũng là tư liệu hữu ích giúp thầy cô tham khảo để soạn giáo án cho riêng mình.

Toán 10: Bài tập cuối chương III - Cánh diều

Giải SGK Toán 10 trang 60 - Tập 1

Giải SGK Toán 10 trang 60 - Tập 1

Bài 1 trang 60

Tìm tập xác định của mỗi hàm số sau:

$a) y = \frac{1}{{{x^2} - x}}$

$b) y = \sqrt {{x^2} - 4x + 3}$

$c) y = \frac{1}{{\sqrt {x - 1} }}$

Gợi ý đáp án

a) $y = \frac{1}{{{x^2} - x}} xác định \Leftrightarrow {x^2} - x \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 1\end{array} \right.$

Tập xác định $D = \mathbb{R}\backslash \left\{ {0;1} \right\}$

b) $y = \sqrt {{x^2} - 4x + 3} xác định \Leftrightarrow {x^2} - 4x + 3 \ge 0 \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x \le 1\end{array} \right.$

Tập xác định $D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)$

c) $y = \frac{1}{{\sqrt {x - 1} }}$ xác định $\Leftrightarrow x - 1 > 0 \Leftrightarrow x > 1$

Bài 2 trang 60

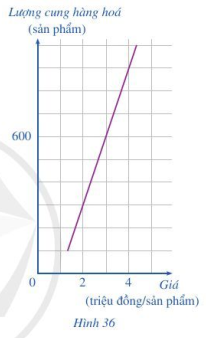
Đồ thị ở Hình 36 cho thấy sự phụ thuộc của lượng hàng hoá được sản xuất (cung) (đơn vị; sản phẩm) bởi giá bán (đơn vị: triệu đồng/sản phẩm) đối với một loại hàng hoá.

a) Xác định lượng hàng hoá được sản xuất khi mức giá bán 1 sản phẩm là 2 triệu đồng; 4 triệu đồng.

b) Biết nhu cầu thị trường đang cần là 600 sản phẩm. Hỏi với mức giá bán là bao nhiêu thì thị trường cân bằng (thị trường cân bằng khi sản lượng cung bằng sản lượng cầu)?

Gợi ý đáp án

a) Từ đồ thị ta thấy khi giá bán là 2 triệu đồng/sản phẩm thì lượng cung hàng hóa là: 300 sản phẩm, khi giá bán là 4 triệu đồng/sản phẩm thì lượng cung hàng hóa là 900 sản phẩm.

b) Khi nhu cầu thị trường là 600 sản phẩm, để cân bằng thị trường thì lượng cung bằng lượng cầu. Khi đó lượng cung hàng hóa cũng là 600 sản phẩm.

Từ đồ thị ta thấy khi lượng cung hàng hóa là 600 sản phẩm thì giá bán là 3 triệu đồng/sản phẩm.

Bài 3 trang 60

Một nhà cung cấp dịch vụ Internet đưa ra hai gói khuyến mại cho người dùng như sau:

Gói A: Giá cước 190 000 đồng/tháng.

Nếu trả tiền cước ngày 6 tháng thì sẽ được tặng thêm 1 tháng.

Nếu trả tiền cước ngày 12 tháng thì sẽ được tặng thêm 2 tháng.

Gói B: Giá cước 189 000 đồng/tháng.

Nếu trả tiền cước ngày 7 tháng thì số tiền phải trả cho 7 tháng đó là 1 134 000 đồng.

Nếu trả tiền cước ngày 15 tháng thì số tiền phải trả cho 15 tháng đó là 2 268 000 đồng.

Giả sử số tháng sử dụng Internet là x (1 nguyên dương).

a) Hãy lập các hàm số thể hiện số tiền phải trả ít nhất theo mỗi gói A, B nếu thời gian

dùng không quá 15 tháng.

b) Nếu gia đình bạn Minh dùng 15 tháng thì nên chọn gói nào?

Gợi ý đáp án

Gói A:

Hàm số:

Gói B:

Hàm số:

$y = \left\{ \begin{array}{l}x.189000\quad \;\quad \quad \;\quad \quad \;\quad \quad 1 \le x \le 6\\1134000 + (x - 7).189000\quad \;7 \le x \le 14\\2268000\quad \;\quad \quad \;\quad \quad \;\quad \quad \;x = 15\end{array} \right.$

Gia đình bạn Minh dùng 15 tháng,

+) Nếu chọn gói A: Số tiền phải trả là $y = (15 - 2).190\;000 = 2\;470\;000$ (đồng)

+) Nếu chọn gói B: Số tiền phải trả là 2268000 đồng.

Vậy gia đình bạn Minh nên chọn gói B.

Bài 4 trang 60

Quan sát đồ thị hàm số bậc hai y = ax² + bx + c ở Hình 37a và Hình 37b rồi nêu:

a) Dấu của hệ số a;

b) Tọa độ đỉnh và trục đối xứng;

c) Khoảng đồng biến;

d) Khoảng nghịch biến;

e) Khoảng giá trị x mà y > 0;

g) Khoảng giá trị x mà y ≤ 0.

Gợi ý đáp án

* Hình 37a: Quan sát đồ thị ta thấy:

a) Bề lõm của đồ thị hướng lên trên nên hệ số a > 0 hay hệ số a mang dấu “+”.

b) Tọa độ đỉnh I(1; – 1), trục đối xứng x = 1.

c) Do hệ số a > 0 nên hàm số đồng biến trên khoảng (1; + ∞).

d) Hàm số nghịch biến trên khoảng (– ∞; 1).

e) Phần parabol nằm phía trên trục hoành tương ứng với các khoảng (– ∞; 0) và (2; + ∞) nên hàm số y > 0 trên các khoảng giá trị của x là (– ∞; 0) ∪ (2; + ∞).

g) Phần parabol phía dưới trục hoành tương ứng với khoảng (0; 2) nên hàm số y < 0 trên (0; 2). Vậy khoảng giá trị của x mà y ≤ 0 là đoạn [0; 2].

* Hình 37b: Quan sát đồ thị ta thấy,

a) Bề lõm của đồ thị hướng xuống dưới nên a < 0 hay hệ số a mang dấu “–”.

b) Tọa độ đỉnh I(1; 4), trục đối xứng x = 1.

c) Do hệ số a < 0 nên hàm số đồng biến trên khoảng (– ∞; 1).

d) Hàm số nghịch biến trên khoảng (1; +∞).

e) Phần parabol nằm phía trên trục hoành tương ứng với khoảng (– 1; 3) nên khoảng giá trị của x là (– 1; 3) thì y > 0.

g) Phần parabol nằm phía dưới trục hoành tương ứng với các khoảng (– ∞; – 1) và (3; + ∞) nên khoảng giá trị của x để y ≤ 0 là (– ∞; – 1] ∪ [3; + ∞).

Bài 5 trang 61

Vẽ đồ thị của mỗi hàm số sau:

$a) y = {x^2} - 3x - 4$

$b) y = {x^2} + 2x + 1$

$c) y = - {x^2} + 2x - 2$

Gợi ý đáp án

$a) y = {x^2} - 3x - 4$

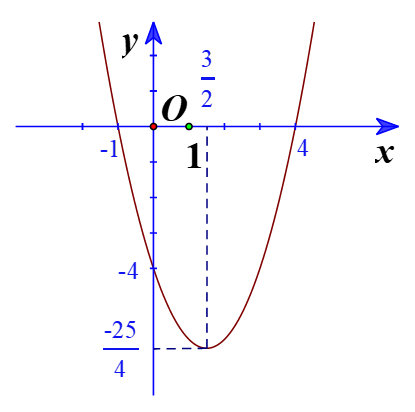
Đồ thị hàm số có đỉnh $I\left( {\dfrac{3}{2}; - \dfrac{{25}}{4}} \right)$

Trục đối xứng là $x = \dfrac{3}{2}$

Giao điểm của parabol với trục tung là (0;-4)

Giao điểm của parabol với trục hoành là (-1;0) và (4;0)

Điểm đối xứng với điểm (0;-4) qua trục đối xứng $x = \frac{3}{2} là (3;-4)$

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

$b) y = {x^2} + 2x + 1$

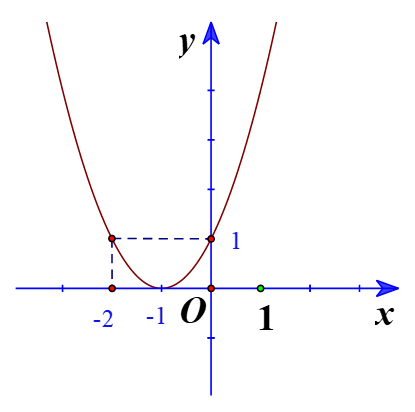
Đồ thị hàm số có đỉnh $I\left( { - 1;0} \right)$

Trục đối xứng là x = - 1

Giao điểm của parabol với trục tung là (0;1)

Giao điểm của parabol với trục hoành là (-1;0)

Điểm đối xứng với điểm (0;1) qua trục đối xứng x = - 1 là (-2;1)

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

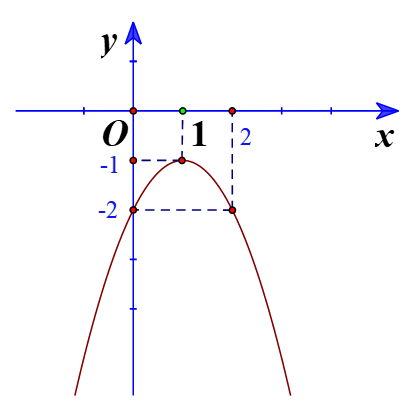
c) y = - {x^2} + 2x - 2

Đồ thị hàm số có đỉnh I\left( {1; - 1} \right)

Trục đối xứng là x = 1

Giao điểm của parabol với trục tung là (0;-2)

Điểm đối xứng với điểm (0;-2) qua trục đối xứng x = 1 là (2;-2)

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

Bài 6 trang 61

Lập bảng xét dấu của mỗi tam thức bậc hai sau:

$a) f\left( x \right) = - 3{x^2} + 4x - 1$

$b) f\left( x \right) = {x^2} - x - 12$

$c) f\left( x \right) = 16{x^2} + 24x + 9$

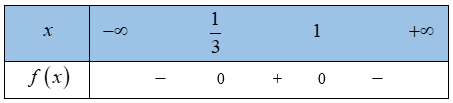
Gợi ý đáp án

$a) f\left( x \right) = - 3{x^2} + 4x - 1$

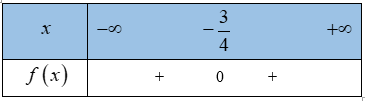
$=> f\left( x \right) có 2 nghiệm x = \frac{1}{3},x = 1$

Bảng xét dấu:

$b) f\left( x \right) = {x^2} - x - 12$

$a = 1 > 0, \Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0$

$=> f\left( x \right)$ có 2 nghiệm x = - 3,x = 4

Bảng xét dấu:

$c) f\left( x \right) = 16{x^2} + 24x + 9$

$a = 16 > 0, \Delta ' = {12^2} - 16.9 = 0$

$=> f\left( x \right)$ có nghiệm duy nhất $x = - \frac{3}{4}$

Bảng xét dấu:

Giải Toán 10 Bài tập cuối chương III trang 60, 61 Cánh diều

Toán 10: Bài tập cuối chương III - Cánh diều

Giải SGK Toán 10 trang 60 - Tập 1

Toán 10: Bài tập cuối chương III - Cánh diều

Giải SGK Toán 10 trang 60 - Tập 1

Bài 1 trang 60

Bài 2 trang 60

Bài 3 trang 60

Bài 4 trang 60

Bài 5 trang 61

Bài 6 trang 61

Liên kết tải về

Chủ đề liên quan

Học tập

Lớp 10

Toán 10 Cánh Diều

Chia sẻ

Có thể bạn quan tâm

Được tải nhiều nhất

Bài viết mới nhất