Bài 1. (2.00 điểm)

1) Rút gọn biểu thức .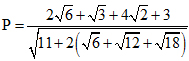

2) Với n là số nguyên dương, cho các biểu thức và

Tính tỉ số A/B.

Bài 2. (2.00 điểm)

1) Giải phương trình .

2) Giải hệ phương trình .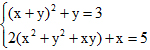

Bài 3. (2.00 điểm)

1) Cho ba số a, b, c thỏa mãn và a³ > 36 và abc = 1. Chứng minh: a² + 3(b² + c²) > 3(ab + bc + ca).

2) Cho a thuộc Z và a ≥ 0. Tìm số phần tử của tập hợp 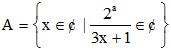(¢ là tập hợp các số nguyên).

Bài 4. (3.00 điểm)

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O; R). Tiếp tuyến tại A của (O; R) cắt đường thẳng BC tại điểm M. Gọi H là chân đường cao hạ từ A xuống BC.

1) Chứng minh AB.AC = 2R.AH.

2) Chứng minh .

3) Trên cạnh BC lấy điểm N tùy ý (N khác B và C). Gọi E, F lần lượt là hình chiếu vuông góc của N lên AB, AC. Tìm vị trí của N để độ dài đoạn EF nhỏ nhất.

Bài 5. (1.00 điểm)

Cho tam giác ABC có đường cao AH, biết H thuộc cạnh BC và BH = BC/3. Trên tia đối của tia HA, lấy điểm K sao cho: . Chứng minh: AK.BC = AB.KC + AC.BK.

Download tài liệu để xem thêm chi tiết.