Bài 1: (4 điểm)

a) Cho a; b là hai số nguyên dương khác nhau, thoả mãn 2a² + a = 3b² + b.

Chứng minh là phân số tối giản.

b) Tìm các cặp số nguyên dương (x; y) thoả mãn: 15x² − 7y² = 9

Bài 2: (4 điểm)

a) Cho

Tính giá trị biểu thức theo a.

b) Cho a, b, c là 3 số dương thoả mãn . Tìm giá trị lớn nhất của Q = abc

Bài 3: (4 điểm)

a) Giải phương trình:

b) Giải hệ phương trình: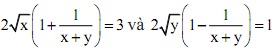

Bài 4: (6 điểm)

Cho nửa đường tròn tâm O đường kính AB cố định. EF là dây cung di động trên nửa đường tròn đó, sao cho E thuộc cung AF và . Gọi H là giao điểm của AF và BE; C là giao điểm của AE và BF; I là giao điểm của CH và AB.

a) Tính số đo góc CIF.

b) Chứng minh rằng biểu thức AE.AC + BF.BC có giá trị không đổi khi EF di động trên nửa đường tròn.

c) Xác định vị trí của EF trên nửa đường tròn để tứ giác ABFE có diện tích lớn nhất. Tính diện tích lớn nhất đó theo R.

Bài 5: (2 điểm)

Tìm cạnh của hình vuông nhỏ nhất, biết rằng: hình vuông đó chứa 5 đường tròn có bán kính bằng 1 và 5 đường tròn này đôi một không có quá 1 điểm chung.

Download tài liệu để xem chi tiết.