MÔN THI: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
--------------------------------------------------------------------------------

Câu 1: (2 điểm)

Cho . Hãy tính:

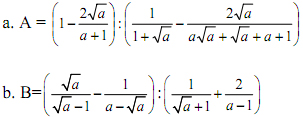
Câu 2: (2 điểm)

Giải phương trình:

Câu 3: (2 điểm)

Cho tam giác ABC, C = 90^o, AB = a, góc A = α, CM, CN lần lượt là đường trung tuyến và đường phân giác của tam giác.

- Tính AC, BC và diện tích các tam giác ABC, CNM.

- Áp dụng với a = 6.56cm và α= 56^o68’.

Câu 4: (2 điểm)

Tìm nghiệm nguyên của phương trình: 6x² + 5y² = 74

Câu 5: (2 điểm)

Tìm tất cả các bộ số nguyên dương (a, b, c) thoả mãn: a³b³ + (a³ - 2ac)b + c(c - a) = 0

Câu 6: (2 điểm)

Giải hệ phương trình: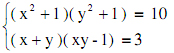

Câu 7: (2 điểm)

Tính tổng:

Câu 8: (2 điểm)

Các đường cao AH, BE và CF của tam giác nhọn ABC cắt đường tròn ngoại tiếp tam giác đó tại các điểm thứhai tương ứng M, N và K.
Tính:

Câu 9: (2 điểm)

Cho . Tìm tất cả các số tự nhiên m, n để P là số nguyên tố.

Câu 10: (2 điểm)

Cho tam giác ABC. O là một điểm bất kỳ nằm trong tam giác. Các tia AO, BO, CO cắt BC, CA và AB lần lượt tại P,Q,R. Tìm giá trị nhỏ nhất của

Download tài liệu để xem thêm chi tiết