Bài 1.

Gọi x₀ là nghiệm của phương trình . Tính các giá trị sau: x₀ = ?, x₀ ≈ ?

Bài 2.

Cho hàm số: . Gọi M là giá trị lớn nhất của hàm số. Hãy tính các giá trị: f(2 + 3√5) và M ≈ ?

Bài 3.

Cho dãy số: 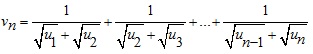, trong đó: u₁ = 1; u_n = u_n-1 + 2 (với mọi n > 1)

a. Tìm công thức tính v_n theo n (với mọi n > 1).

b. Tính giá trị v₂₀₁₀ = ?

Bài 4.

Cho tứ giác lồi ABCD có diện tích bằng . Trên các cạnh AB, BC, CD, DA lấy các điểm tương ứng K, L, M, N sao cho AK : KB = 2, BL : LC = 1 : 3, CM : MD = 1, DN : NA = 1: 2. Tính diện tích đa giác AKLCMN theo đơn vị cm².

Bài 5.

Một hình vuông và một hình tam giác đều cùng nội tiếp một hình tròn có bán kính bằng 1cm, sao cho một cạnh của tam giác song song với một cạnh của hình vuông. Gọi S là diện tích phần chung của tam giác và hình vuông. Hãy tính các giá trị S = ?, S ≈ ?

Bài 6.

Cho ngũ giác lồi ABCDE, biết diện tích các tam giác: ABC, BCD, CDE, DEA, EAB đều bằng 1cm². Gọi s(X) là diện tích của hình X. Hãy thực hiện các yêu cầu

Bài 7.

Cho dãy số vô hạn sau: các số hạng của dãy được sắp xếp giảm dần và đánh số thứ tự bắt đầu từ 1. Gọi a_n là số hạng thứ n; S_n là tổng n số hạng đầu tiên của dãy. Hãy tính: a_n, S₂₀₁₀

Bài 8.

a) Cho đa thức P(x) = x¹¹ + a₁₀x¹⁰ + ... + a₁x +m. Biết rằng: P(i) = i, với mọi i = 1, 2, 3, 4, ..., 11; a_j thuộc Z. Nêu tóm tắt cách tính và tính chính xác giá trị P(12).

b) Xét dãy các số nguyên x₁ = 34, x₂ = 334, x₃ = 3334,..., x_n = 33..34, trong đó x_n có n chữ số 3 và chữ số hàng đơn vị là 4. Gọi S(n) là số chữ số 3 có mặt trong số 9(x_n)³. Nêu cách tính S(n) và tính S(2010)

Bài 9.

Cho . Tính giá trị f₂₀₀₉(2010)?

Bài 10.

Đặt (với n dấu căn lồng nhau, dấu * được thay thế bởi một trong hai dấu cộng (+) hoặc trừ (-) sao cho quét hết các khả năng biểu diễn. Ví dụ:

Download tài liệu để xem thêm chi tiết.