Hình chóp đều là loại hình học không gian khó và khá phức tạp và đây cũng là một trong những kiến thức trọng tâm quan trọng trong các kỳ thi. Vậy hình chóp đều là gì? Công thức tính diện tích hình chóp đều như thế nào? Mời các bạn cùng theo dõi bài viết dưới đây của Download.vn.
Trong bài viết dưới đây chúng tôi sẽ giới thiệu đến các bạn chi tiết về định nghĩa hình chóp đều, công thức tính diện tích xung quanh, công thức tính diện tích toàn phần và thể tích kèm theo ví dụ minh họa, bài tập. Hi vọng qua tài liệu này các bạn nhanh chóng biết vận dụng vào tính toán diện tích, thể tích hình chóp đều. Bên cạnh đó các bạn xem thêm công thức tính khối chóp.
Các công thức về hình chóp đều
1. Hình chóp đều là gì
Hình chóp đều là hình chóp có đáy là đa giác đều; các cạnh bên bằng nhau . (Nếu định nghĩa như thế này thì Hình chóp đều cũng chính là Hình chóp đa giác đều. Vì Khi có đáy là đa giác đều và các cạnh bên bằng nhau, ta có thể dễ dàng chứng minh được rằng Hình chiếu của đỉnh trên đáy cũng chính là Tâm của đa giác đáy.
2. Công thức diện tích hình chóp đều
a) Diện tích xung quanh của hình chóp đều
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p.d (p: nửa chu vi đáy, d: trung đoạn)
b) Diện tích toàn phần của hình chóp
Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy:
Stp = Sxq + S (S: diện tích đáy)
3. Công thức thể tích hình chóp đều
Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao:
V = 1/3S.h (S: diện tích đáy, h: chiều cao)
4. Ví dụ áp dụng
Ví dụ: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 8cm, chiều cao 10cm.
+ Tính diện tích xung quanh và diện tích toàn phần của hình chóp.
+ Tính thể tích của hình chóp.
Hướng dẫn:
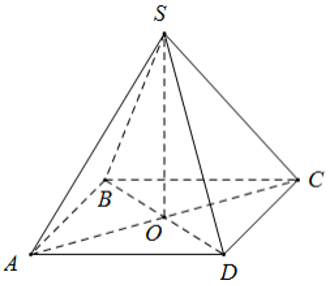
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
![]()
+ BD = AC = √ (82 + 82) = 8√ 2 cm ⇒ AO = BO = CO = DO = 4√ 2 cm
Do đó:
+ Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 cm2
+ Diện tích toàn phần của hình chóp đều là
Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 cm2
+ Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3cm3
5. Bài tập trắc nghiệm về hình chóp đều
Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là?
A. 6cm3
B. 18 cm3
C. 12 cm3
D. 9 cm3
Áp dụng công thức thể tích của hình chóp ta có:
V = 1/3h.SABCD = 1/3.2.32 = 6 cm3
Chọn đáp án A.
Bài 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 4cm,BC = 5cm. Biết thể tích của hình chóp S.ABCD bằng 36 cm3. Tính độ dài đường cao của hình chóp?
A. 6 cm
B. 8 cm
C. 5,4 cm
D. 7,2 cm
Áp dụng công thức thể tích của hình chóp ta có:
V = 1/3.h.SABCD
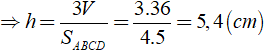
Chọn đáp án C.
Bài 3: Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh bằng 4cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm. Diện tích xung quanh của hình chóp đã cho là?
A. 32 cm2
B. 32√ 2 cm2
C. 16√ 2 cm2
D. 16 cm2
Chu vi của đáy ABCD là 2(4 + 4) = 16 cm
Gọi d là độ dài trung đoạn của hình chóp
Ta có: d = √ (62 - 22) = 4√ 2 cm
Áp dụng công thức diện tích xung quanh của hình chóp: Sxq = p.d
⇒ Sxq = 8.4√ 2 = 32√ 2 cm2
Chọn đáp án B.
