Bộ đề thi học sinh giỏi lớp 12 môn Toán cấp Tỉnh, TP dành cho các bạn học sinh lớp 12 giúp các em ôn tập lại các kiến thức đã học và đồng thời giáo viên cũng có thêm tư liệu tham khảo trong việc ra đề thi. Chúc các bạn đạt kết quả cao trong kỳ thi học sinh giỏi lớp 12 sắp tới.

Câu 1. (4,0 điểm)

1) Cho hàm số: có đồ thị là (C). Tìm tọa độ điểm M thuộc đồ thị (C) sao cho tổng khoảng cách từ điểm M đến hai đường tiệm cận đạt giá trị nhỏ nhất.

2) Cho hàm số: y = 2x³ - (m + 6)x² - (m² - 3m) x + 3m² có đồ thị là (Cm) ( m là tham số). Tìm tất cả các giá trị của m sao cho đồ thị (Cm ) cắt trục hoành tại ba điểm phân biệt có hoành độ x₁; x₂; x₃ thỏa mãn: (x1 -1)² + x₂ -1)² + (x₃-1)² = 6.

Câu 2. (4,0 điểm)

1) Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O (n ∈ N*, n ≥ 2). Gọi S là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn được một tam giác vuông trong tập S là 1/3. Tìm n.

2) Tính tổng tất cả các nghiệm thuộc [0;100] của phương trình:

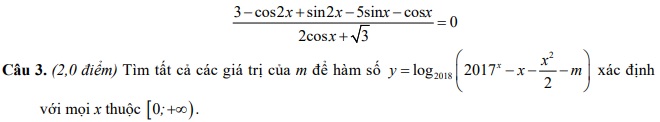
Câu 4. (6,0 điểm)

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a, góc ABC = 60, SA = SB = SC, SD = 2a. Gọi (P) là mặt phẳng qua A và vuông góc với SB tại K.

1) Tính khoảng cách từ điểm A đến mặt phẳng (SCD).

2) Mặt phẳng (P) chia khối chóp S.ABCD thành hai phần có thể tích V₁; V₂ trong đó V₁ là thể tích khối đa diện chứa đỉnh S. Tính V₁/V₂

3) Gọi M, N theo thứ tự là hình chiếu vuông góc của K trên SC và SA. Tính diện tích mặt cầu ngoại tiếp khối chóp K.ACMN.

Câu 5. (2,0 điểm) Giải hệ phương trình:

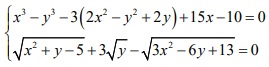
Câu 6. (2,0 điểm)

Cho a,b,c,d là các số thực không âm và có tổng bằng 1. Tìm giá trị nhỏ nhất của biểu thức:

P = (1 + a² + b2 + a2b²)(1 + c2 + d2 + c2d²)

---HẾT---

Mời các bạn tải về để xem trọn bộ tài liệu