Bài 2 trang 18 Toán 10 Cánh diều

Giải Bài 2 trang 18 Toán 10 cánh diều giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi Luyện tập vận dụng và 8 bài tập trong SGK bài Tập hợp - Các phép toán trên tập hợp.

Giải Toán 10 Cánh diều trang 18 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán 10 tập 1. Giải Toán 10 tập 1 trang 18 là tài liệu cực kì hữu ích hỗ trợ các em học sinh lớp 10 trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp

I. Giải Toán lớp 10 bài 2 phần Luyện tập vận dụng

II. Giải Bài 2 trang 18 Toán 10 Cánh diều

I. Giải Toán lớp 10 bài 2 phần Luyện tập vận dụng

Luyện tập 1

êu số phần tử của mỗi tập hợp sau:

G = {x ∈ R | x² + 1 = 0},

N* = {1; 2; 3; …}

Lời giải:

Vì x² ≥ 0 ∀ x ∈ R nên x² + 1 ≥ 1 > 0 ∀ x ∈ R

Vậy tập hợp G không có phần tử nào hay G = ∅.

+ N* là tập hợp các số tự nhiên khác 0 nên tập hợp N* có vô số phần tử.

Luyện tập 2

Cho hai tập hợp:

A = {n ∈ $\mathbb{N}$ | n chia hết cho 3},

B = {n ∈ $\mathbb{N}$ | n chia hết cho 9}.

Chứng tỏ B ⊂ A.

Lời giải:

n chia hết cho 9 nên n = 9k với k ∈ $\mathbb{N}$ .

Có n = 9k = 3.3k hay n chia hết cho 3.

Vậy nếu n chia hết cho 9 thì n chia hết cho 3.

→ Mọi phần tử thuộc tập hợp B đều thuộc tập hợp A.

Luyện tập 3

Cho hai tập hợp:

E = {n ∈ $\mathbb{N}$ | n chia hết cho 3 và 4} và G = {n ∈ N| n chia hết cho 12}.

Chứng tỏ rằng E = G

Lời giải:

+ n chia hết cho 3 và 4 nên n là bội chung của 3 và 4. Ta có n = 3.4.k với k ∈ $\mathbb{N}$ .

Có n = 3.4.k = 12k hay n chia hết cho 12.

Vậy nếu n chia hết cho 3 và 4 thì n chia hết cho 12.

→ Mọi phần tử thuộc tập hợp E đều thuộc tập hợp G.

Vậy E ⊂ G (1)

+ n chia hết cho 12 nên n = 12k với k ∈ $\mathbb{N}$ .

Có n = 12k = 3.4.k hay n chia hết cho 3 và n chia hết cho 4.

Vậy nếu n chia hết cho 12 thì n chia hết cho 3 và 4.

→ Mọi phần tử thuộc tập hợp G đều thuộc tập hợp E.

Vậy G ⊂ E (2)

Từ (1) và (2) suy ra E = G.

Luyện tập 4

Cho hai tập hợp:

A = {x ∈ $\mathbb{R}$ | x ≤ 0}, B = { x ∈ $\mathbb{R}$ | x ≥ 0}

Tìm A ∩ B, A ∪ B.

Lời giải:

A ∩ B = {0}

A ∪ B =R

II. Giải Bài 2 trang 18 Toán 10 Cánh diều

Bài 1 trang 18

Cho tập hợp X = {a; b; c}. Viết tất cả các tập con của tập hợp X.

Lời giải:

Các tập hợp con của tập hợp X = {a; b; c} là:

X, {a}, {b}, {c}, {a; b}, {a; c}, {b; c}.

Bài 2 trang 18

Sắp xếp các tập hợp sau theo quan hệ “⊂”: [2; 5], (2; 5), [2; 5), (1; 5]

Lời giải:

Tập hợp [2; 5] là tập hợp gồm các số thực lớn hơn hoặc bằng 2 và nhỏ hơn hoặc bằng 5.

Tập hợp (2; 5) là tập hợp gồm các số thực lớn hơn 2 và nhỏ hơn 5.

Tập hợp [2; 5) là tập hợp gồm các số thực lớn hơn hoặc bằng 2 và nhỏ hơn 5.

Tập hợp (1; 5] là tập hợp các số thực lớn hơn 1 và nhỏ hơn hoặc bằng 5.

Do đó ta sắp xếp các tập hợp như sau:

(2; 5) ⊂ [2; 5) ⊂ [2; 5] ⊂ (1; 5].

Bài 3 trang 18

Xác định các tập hợp sau và biểu diễn chúng trên trục số:

$a) [ - 3;7] \cap (2;5)$

$b) ( - \infty ;0] \cup ( - 1;2)$

$c) \mathbb{R}\,{\rm{\backslash }}\,( - \infty ;3)$

$d) ( - 3;2)\,{\rm{\backslash }}\,[1;3)$

Gợi ý đáp án

a) Đặt $A = [ - 3;7] \cap (2;5)$

Tập hợp A là khoảng (2; 5) và được biểu diễn là:

b) Đặt $B = ( - \infty ;0] \cup ( - 1;2)$

Tập hợp B là khoảng ( - \infty ;2) và được biểu diễn là:

c) Đặt $C = \mathbb{R}\,{\rm{\backslash }}\,( - \infty ;3)$

Tập hợp C là nửa khoảng $[3; + \infty )$ và được biểu diễn là:

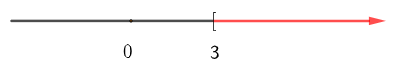
d) Đặt $D = ( - 3;2)\,{\rm{\backslash }}\,[1;3)$

Tập hợp D là khoảng ( - 3;1) và được biểu diễn là:

Bài 4 trang 18

Gọi A là tập nghiệm của phương trình ${x^2} + x - 2 = 0,$

B là tập nghiệm của phương trình $2{x^2} + x - 6 = 0$

Tìm $C = A \cap B.$

Gợi ý đáp án

Ta có: ${x^2} + x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.$

$\Rightarrow A = \{ 1; - 2\}$

Ta có: $2{x^2} + x - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{3}{2}\\x = - 2\end{array} \right.$

$\Rightarrow B = \left\{ {\frac{3}{2}; - 2} \right\}$

Vậy $C = A \cap B = \{ - 2\} .$

Bài 5 trang 18

Tìm $D = E \cap G$ biết E và G lần lượt là tập nghiệm của hai bất phương trình trong mỗi trường hợp sau:

a) $2x + 3 \ge 0$ và $- x + 5 \ge 0$

b) x + 2 > 0 và 2x - 9 < 0

Gợi ý đáp án

a) Ta có: $2x + 3 \ge 0 \Leftrightarrow x \ge \frac{{ - 3}}{2}$

$\Rightarrow$ Tập hợp E là: $E = \left\{ {x \in \mathbb{R}|x \ge \frac{{ - 3}}{2}} \right\}$

và $- x + 5 \ge 0 \Leftrightarrow x \le 5$

$\Rightarrow$ Tập hợp G là $G = \left\{ {x \in \mathbb{R}|x \le 5} \right\}$

$\Rightarrow E \cap G = {x \in \mathbb{R}|x \ge \frac{{ - 3}}{2} và x \le 5} = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\}$

Vậy tập hợp $D = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\}$

Bài 6 trang 18

Gọi A là tập nghiệm của đa thức P(x). Viết tập hợp các số thực x sao cho biểu thức $\dfrac{1}{{P(x)}}$ xác định.

Gợi ý đáp án

Ta có: A là tập nghiệm của đa thức P(x)

$\Rightarrow A = \{ x \in \mathbb{R}|P(x) = 0\}$

Để biểu thức $\dfrac{1}{{P(x)}}$ xác định thì $P(x) \ne 0$ hay $x \notin A.$

Gọi B là tập hợp các số thực x sao cho biểu thức $\dfrac{1}{{P(x)}}$ xác định.

$\Rightarrow B = \left\{ {x \in \mathbb{R}|x \notin A} \right\} = \mathbb{R}\,{\rm{\backslash }}\,A hay B = \{ x \in \mathbb{R}|P(x) \ne 0\}$

Bài 7 trang 18

Lớp 10B có 28 học sinh tham gia câu lạc bộ thể thao và 19 học sinh tham gia câu lạc bộ âm nhạc. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên.

a) Có bao nhiêu học sinh ở lớp 10B tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc?

b) Có bao nhiêu học sinh ở lớp 10B tham gia ít nhất một trong hai câu lạc bộ trên?

c) Biết lớp 10B có 40 học sinh. Có bao nhiêu học sinh không tham gia câu lạc bộ thể thao? Có bao nhiêu học sinh không tham gia cả hai câu lạc bộ?

Gợi ý đáp án

a) Trong 28 học sinh tham gia câu lạc bộ thể thao có 10 học sinh tham gia cả câu lạc bộ âm nhạc

Vậy có 28-10=18 học sinh chỉ tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc

b) Số học sinh tham gia ít nhất một trong hai câu lạc bộ trên là: 28 + 19 – 10 = 37 (học sinh)

c) Cả lớp có 40 học sinh, trong đó có 28 học sinh tham gia câu lạc bộ thể thao.

Do đó số học sinh không tham gia câu lạc bộ thể thao là: 40 – 28 = 12 (học sinh)

Cả lớp có 40 học sinh, trong đó có 37 học sinh tham gia ít nhất một trong hai câu lạc bộ.

Vậy số học sinh không tham gia cả hai câu lạc bộ là: 40 – 37 = 3 (học sinh)

Bài 8 trang 18

Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? Biết có 4 học sinh của nhóm không tham gia tiết mục nào.

Gợi ý đáp án

Vì nhóm có 12 học sinh, trong đó có 4 học sinh không tham gia tiết mục nào nên tổng số học sinh tham gia hai tiết mục múa và hát là: 12 – 4 = 8 (học sinh)

Lại có: Trong 5 học sinh tham gia tiết mục múa, có 3 học sinh tham gia cả hai tiết mục

Vậy số học sinh chỉ tham gia tiết mục múa là: 5 – 3 = 2 (học sinh)

Do đó số học sinh tham gia tiết mục hát là: 8 – 2 = 6 (học sinh)

Vậy trong nhóm có 6 học sinh tham gia tiết mục hát.

Bài 2 trang 18 Toán 10 Cánh diều - Tập 1

Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp

Giải SGK Toán 10 trang 18 - Tập 1 sách Cánh diều

Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp

I. Giải Toán lớp 10 bài 2 phần Luyện tập vận dụng

Luyện tập 1

Luyện tập 2

Luyện tập 3

Luyện tập 4

II. Giải Bài 2 trang 18 Toán 10 Cánh diều

Bài 1 trang 18

Bài 2 trang 18

Bài 3 trang 18

Bài 4 trang 18

Bài 5 trang 18

Bài 6 trang 18

Bài 7 trang 18

Bài 8 trang 18

Liên kết tải về

Chủ đề liên quan

Học tập

Lớp 10

Toán 10 Cánh Diều

Chia sẻ

Có thể bạn quan tâm

Được tải nhiều nhất

Bài viết mới nhất