Cho đường tròn (C): (x – 1)2 + (y – 2)2 = 25 và điểm M(4; – 2). a) Chứng minh điểm M(4; – 2) thuộc đường tròn (C). b) Xác định tâm và bán kính của (C). c) Gọi ∆ là tiếp tuyến của (...
Câu hỏi :
Cho đường tròn (C): (x – 1)2 + (y – 2)2 = 25 và điểm M(4; – 2).
a) Chứng minh điểm M(4; – 2) thuộc đường tròn (C).
b) Xác định tâm và bán kính của (C).
c) Gọi ∆ là tiếp tuyến của (C) tại M. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆ (H.7.16). Từ đó, viết phương trình đường thẳng ∆.
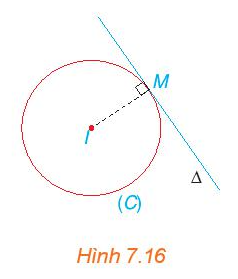
Cho đường tròn (C): (x – 1)2 + (y – 2)2 = 25 và điểm M(4; – 2).
a) Chứng minh điểm M(4; – 2) thuộc đường tròn (C).
b) Xác định tâm và bán kính của (C).
c) Gọi ∆ là tiếp tuyến của (C) tại M. Hãy chỉ ra một vectơ pháp tuyến của đường thẳng ∆ (H.7.16). Từ đó, viết phương trình đường thẳng ∆.

* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
a) Thay tọa độ điểm M(4; – 2) vào phương trình đường tròn (C) ta được:
(4 – 1)2 + (– 2 – 2)2 = 25 ⇔ 32 + (– 4)2 = 25 ⇔ 25 = 25 (luôn đúng).
Vậy điểm M(4; – 2) thuộc đường tròn (C).
b) Đường tròn (C) có tâm I(1; 2) và bán kính R = \(\sqrt {25} \) = 5.
c) Ta có: ∆ ⊥ IM tại M (bán kính đi qua tiếp điểm thì vuông góc với tiếp tuyến tại tiếp điểm đó).
Do đó một vectơ pháp tuyến của đường thẳng ∆ là vectơ \(\overrightarrow {IM} = \left( {4 - 1;\, - 2 - 2} \right) = \left( {3;\, - 4} \right)\).
Đường thẳng ∆ đi qua điểm M(4; – 2) và có một vectơ pháp tuyến \(\overrightarrow {IM} = \left( {3;\, - 4} \right)\) nên phương trình đường thẳng ∆ là: 3(x – 4) – 4(y + 2) = 0 hay 3x – 4y – 20 = 0.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 21. Đường tròn trong mặt phẳng tọa độ có đáp án !!
Bạn có biết?
Toán học là môn khoa học nghiên cứu về các số, cấu trúc, không gian và các phép biến đổi. Nói một cách khác, người ta cho rằng đó là môn học về "hình và số". Theo quan điểm chính thống neonics, nó là môn học nghiên cứu về các cấu trúc trừu tượng định nghĩa từ các tiên đề, bằng cách sử dụng luận lý học (lôgic) và ký hiệu toán học. Các quan điểm khác của nó được miêu tả trong triết học toán. Do khả năng ứng dụng rộng rãi trong nhiều khoa học, toán học được mệnh danh là "ngôn ngữ của vũ trụ".
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 10
Lớp 10 - Năm thứ nhất ở cấp trung học phổ thông, năm đầu tiên nên có nhiều bạn bè mới đến từ những nơi xa hơn vì ngôi trường mới lại mỗi lúc lại xa nhà mình hơn. Được biết bên ngoài kia là một thế giới mới to và nhiều điều thú vị, một trang mới đang chò đợi chúng ta.
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
