Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4 km. Hằng tuần bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này...
Câu hỏi :
Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4 km. Hằng tuần bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này, do trục trặc về vận chuyển nên toàn bộ số hàng vẫn đang nằm ở thôn Hoành, bên bờ biển cách bến Bính 9,25 km và sẽ được anh Nam vận chuyển trên con đường dọc bờ biển tới bến Bính bằng xe kéo. Bác Việt đã gọi điện thống nhất với anh Nam là họ sẽ gặp nhau ở vị trí nào đó giữa bến Bính và thôn Hoành để hai người có mặt tại đó cùng lúc, không mất thời gian chờ nhau. Giả thiết rằng đường dọc bờ biển là thẳng và bác Việt cũng di chuyển theo một đường thẳng để tới điểm hẹn. Tìm vị trí hai người hẹn gặp, biết rằng vận tốc của anh Nam là 5 km/h và của bác Việt là 4 km/h.
Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4 km. Hằng tuần bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này, do trục trặc về vận chuyển nên toàn bộ số hàng vẫn đang nằm ở thôn Hoành, bên bờ biển cách bến Bính 9,25 km và sẽ được anh Nam vận chuyển trên con đường dọc bờ biển tới bến Bính bằng xe kéo. Bác Việt đã gọi điện thống nhất với anh Nam là họ sẽ gặp nhau ở vị trí nào đó giữa bến Bính và thôn Hoành để hai người có mặt tại đó cùng lúc, không mất thời gian chờ nhau. Giả thiết rằng đường dọc bờ biển là thẳng và bác Việt cũng di chuyển theo một đường thẳng để tới điểm hẹn. Tìm vị trí hai người hẹn gặp, biết rằng vận tốc của anh Nam là 5 km/h và của bác Việt là 4 km/h.
* Đáp án
* Hướng dẫn giải
Hướng dẫn
Ta mô hình hóa bài toán như trong Hình 6.20: Trạm hải đăng ở vị trí A; bến Bính ở B và thôn Hoành ở C.
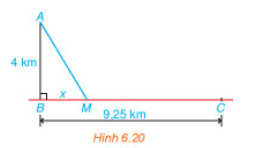
Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM = x (km) (x > 0). Để hai người không phải chờ nhau thì thời gian chèo thuyền bằng thời gian kéo xe nên ta có phương trình:
\(\frac{{\sqrt {{x^2} + 16} }}{4} = \frac{{9,25 - x}}{5}\).
Giải phương trình này sẽ tìm được vị trí hai người dự định gặp nhau.
Hướng dẫn giải
Ta mô hình hóa bài toán như trong Hình 6.20: Trạm hải đăng ở vị trí A; bến Bính ở B và thôn Hoành ở C.
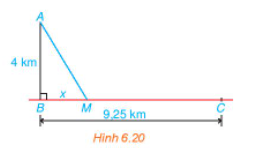
Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM = x (km) (x > 0).
Ta có: BC = BM + MC ⇔ MC = BC – BM = 9,25 – x (km) hay quãng đường của anh Nam từ thôn Hoành đến điểm gặp nhau của 2 người là 9,25 – x (km).
Vận tốc của anh Nam là 5 km/h nên thời gian di chuyển của anh Nam đến điểm hẹn gặp nhau là: \(\frac{{9,25 - x}}{5}\) (giờ).
Tam giác ABC vuông tại B, theo định lí Pythagore ta có:
AM2 = AB2 + BM2 = 42 + x2 = x2 + 16
Suy ra AM = \(\sqrt {{x^2} + 16} \) (km) hay quãng đường di chuyển của bác Việt đến điểm hẹn là \(\sqrt {{x^2} + 16} \) (km).
Vận tốc của bác Việt là 4 km/h nên thời gian di chuyển của bác Việt tới điểm hẹn gặp nhau là: \(\frac{{\sqrt {{x^2} + 16} }}{4}\) (giờ).
Để hai người không phải chờ nhau thì thời gian chèo thuyền bằng thời gian kéo xe nên ta có phương trình:
\(\frac{{\sqrt {{x^2} + 16} }}{4} = \frac{{9,25 - x}}{5}\) (1).
Giải phương trình trên ta có:
(1) \( \Leftrightarrow 5\sqrt {{x^2} + 16} = 37 - 4x\)
Bình phương hai vế phương trình trên ta được:
25(x2 + 16) = 1369 – 296x + 16x2
⇔ 9x2 + 296x – 969 = 0
⇔ x = 3 hoặc x = \( - \frac{{323}}{9}\)
Thử lại ta thấy cả hai giá trị x = 3 và x = \( - \frac{{323}}{9}\) đều thỏa mãn phương trình (1).
Mà điều kiện của x là x > 0 nên ta chọn x = 3.
Vậy vị trí hai người hẹn gặp nhau cách bến Bính 3 km hay cách thôn Hoành 6,25 km.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 18. Phương trình quy về phương trình bậc hai có đáp án !!
Bạn có biết?
Toán học là môn khoa học nghiên cứu về các số, cấu trúc, không gian và các phép biến đổi. Nói một cách khác, người ta cho rằng đó là môn học về "hình và số". Theo quan điểm chính thống neonics, nó là môn học nghiên cứu về các cấu trúc trừu tượng định nghĩa từ các tiên đề, bằng cách sử dụng luận lý học (lôgic) và ký hiệu toán học. Các quan điểm khác của nó được miêu tả trong triết học toán. Do khả năng ứng dụng rộng rãi trong nhiều khoa học, toán học được mệnh danh là "ngôn ngữ của vũ trụ".
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 10
Lớp 10 - Năm thứ nhất ở cấp trung học phổ thông, năm đầu tiên nên có nhiều bạn bè mới đến từ những nơi xa hơn vì ngôi trường mới lại mỗi lúc lại xa nhà mình hơn. Được biết bên ngoài kia là một thế giới mới to và nhiều điều thú vị, một trang mới đang chò đợi chúng ta.
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
