Hình học 12 Bài 2: Phương trình mặt phẳng

a) Biểu thức tọa độ tích có hướng

Cho hai vectơ \(\vec{a}=(x_1;y_1;z_1)\) và \(\vec{b}=(x_2;y_2;z_2)\), vectơ \(\overrightarrow n = \left[ {\overrightarrow a ;\overrightarrow b } \right]\) được gọi là tích có hướng của hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\) được xác định như sau:

\(\left[ {\vec a,\vec b} \right] = \left( {\left| {\begin{array}{*{20}{c}}
{{y_1}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {z_1}}\\
{{y_2}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {z_2}}
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
{{z_1}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {x_1}}\\
{{z_2}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {x_2}}
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
{{x_1}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {y_1}}\\
{{x_2}\;{\mkern 1mu} \;{\mkern 1mu} \;{\mkern 1mu} {y_2}}
\end{array}} \right|} \right) = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\)

b) Tính chất 

Vectơ \(\overrightarrow n\) vuông góc với cả hai vectơ  \(\overrightarrow a\) và \(\overrightarrow b.\)

c) Ứng dụng của tích có hướng

• Chứng minh tính đồng phẳng của vectơ:
  • \(\vec{a},\vec{b},\vec{c}\) không đồng phẳng khi và chỉ khi \(\left [ \vec{a},\vec{b} \right ].\vec{c}\neq 0.\) Suy ra 4 điểm A, B, C, D không đồng phẳng khi và chỉ khi \(\left [ \overrightarrow{AB},\overrightarrow{AC} \right ].\overrightarrow{AD}\neq 0\).
  • \(\vec{a},\vec{b},\vec{c}\) đồng phẳng khi và chỉ khi \(\left [ \vec{a},\vec{b} \right ].\vec{c}= 0\). Suy ra A, B, C, D đồng phẳng khi và chỉ khi \(\left [ \overrightarrow{AB};\overrightarrow{AC} \right ].\overrightarrow{AD}=0\).
• Tính diện tích tam giác và hình bình hành:
  • Diện tích hình bình hành ABCD: \(S_{ABCD}=\left | \left [ \overrightarrow{AB};\overrightarrow{AC} \right ] \right |\).
  • Diện tích tam giác \(\Delta ABC\): \(S_{\Delta ABC}=\frac{1}{2}\left | \left [ \overrightarrow{AB};\overrightarrow{AC} \right ] \right |\).

a) Vectơ pháp tuyến của mặt phẳng

Cho mặt phẳng (P). Nếu vectơ \(\vec n\) khác \(\vec 0\) có giá vuông góc với (P) thì \(\vec n\) được gọi là Vectơ pháp tuyến của của (P).

b) Phương trình tổng quát của mặt phẳng

Phương trình tổng quát của mặt phẳng có dạng: \(Ax+By+Cz+D=0, \,\, A^2+B^2+C^2\neq 0)\).
Với \(\overrightarrow{n}=(A;B;C)\) là Vectơ pháp tuyến (VTPT).

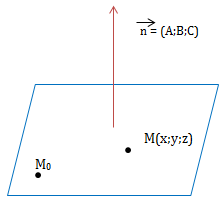
c) Viết phương trình mặt phẳng khi biết Vectơ pháp tuyến và một điểm thuộc mặt phẳng đó

Mặt phẳng (P) đi qua điểm \({{M_0}({x_0};{y_0};{z_0})}\), nhận vectơ \({\vec n = (A;B;C)}\) làm VTPT có phương trình tổng quát là:

\(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)

d) Phương trình mặt phẳng theo đoạn chắn

Mặt phẳng (P) đi qua A(a;0;0), B(0;b;0), C(0;0;c) có phương trình tổng quát là: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\).

e) Một số cách xác định Vectơ pháp tuyến của mặt phẳng

• Gọi \(\vec n\) là VTPT của mặt phẳng (P), giải sử tồn tại \(\vec u_1\) và \(\vec u_2\) sao cho \(\left.\begin{matrix} \vec{n}\perp \overrightarrow{u_1}\\ \vec{n}\perp \overrightarrow{u_2} \end{matrix}\right\}\) thì \(\vec{n}=\left [ \overrightarrow{u_1}; \overrightarrow{u_2} \right ]\) là một VTPT của mặt phẳng (P).
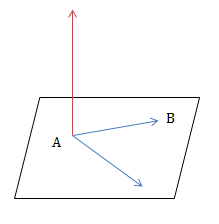
• Mặt phẳng (ABC) có một VTPT \(\vec{n}=\left [ \overrightarrow{AB};\overrightarrow{AC} \right ]\).

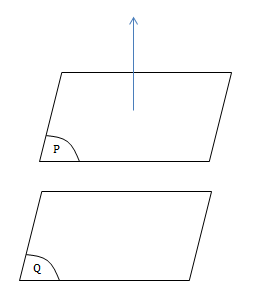
• Mặt phẳng (P) song song với mặt phẳng (Q):
  • ​Gọi: \(\overrightarrow{n}_P\) là một VTPT của (P), \(\overrightarrow{n}_Q\) là một VTPT của (Q) khi đó: \(\overrightarrow{n}_P=\overrightarrow{n}_Q.\)

 

• Cho đường thẳng AB và mặt phẳng (P): \(\bigg \lbrack \begin{matrix} AB\subset (P)\\ AB //(P) \end{matrix}\) thì \(\vec{n_P}\perp \overrightarrow{AB}.\)

 

• Nếu \((P)\perp (Q)\) thì \(\overrightarrow{n}_P\perp \overrightarrow{n}_Q\).

Cho hai mặt phẳng \((\alpha _1) \ A_1x+B_1y+C_1z+D_1=0\) có một VTPT \(\vec{n_1}=(A_1;B_1;C_1)\) và \((\alpha _2) \ A_2x+B_2y+C_2z+D_2=0\) có một VTPT \(\vec{n_2}=(A_2;B_2;C_2)\).

Khi đó vị trí tương đối giữa \((\alpha_1)\) và \((\alpha_2)\) được xác định như sau:

• \((\alpha _1)//(\alpha _2)\) khi và chỉ khi \(\left\{\begin{matrix} \vec{n_1}=k.\vec{n_2}\\ D_1\neq D_2 \end{matrix}\right.\).

Nếu \(A_2, B_2, C_2, D_2 \neq 0\): \((\alpha _1)//(\alpha _2)\Leftrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}\neq \frac{D_1}{D_2}\).

• \((\alpha _1)\equiv (\alpha _2)\) khi và chỉ khi  \(\left\{\begin{matrix} \vec{n_1}=k.\vec{n_2}\\ D_1=k. D_2 \end{matrix}\right.\).

Nếu \(A_2, B_2, C_2, D_2 \neq 0\) thì \((\alpha _1)\equiv (\alpha _2)\Leftrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}= \frac{D_1}{D_2}\).

• \((\alpha _1),(\alpha _2)\) cắt nhau khi và chỉ khi \(\vec{n_1}\neq k.\vec{n_2}\).

​Nếu \(A_2,B_2,C_2\neq 0\) thì \((\alpha _1),(\alpha _2)\) cắt nhau \(\Leftrightarrow \Bigg \lbrack\begin{matrix} \frac{A_1}{A_2} \neq \frac{B_1}{B_2}\\ \frac{A_1}{A_2} \neq \frac{C_1}{C_2}\\ \frac{B_1}{B_2} \neq \frac{C_1}{C_2} \end{matrix}\).

Cho mặt phẳng (P): \(Ax+By+Cz+D=0 \ \ (A^2+B^2+C^2\neq 0)\)
và điểm \(M(x_0,y_0,z_0)\).
Khoảng cách từ M đến (P) được xác định bởi công thức: \(d(M;(P))=\frac{\left | Ax_0+Ay_0+Az_0+D \right |}{\sqrt{A^2+B^2+C^2}}\).

Cho hai mặt phẳng \((P)\;{A_1}x + {B_1}y + {C_1}z + {D_1} = 0\) và \((Q)\;{A_2}x + {B_2}y + {C_2}z + {D_2} = 0\) có VTPT lần lượt là:

\(\vec{n}_P=(A_1;B_1;C_1)\) và \(\vec{n}_Q=(A_2;B_2;C_2)\), khi đó:

​\(cos\widehat {(P,Q)} = \left| {cos({{\vec n}_P};{{\vec n}_Q})} \right| = \frac{{\left| {{{\vec n}_P}.{{\vec n}_Q}} \right|}}{{\left| {{{\vec n}_P}} \right|\left| {{{\vec n}_Q}} \right|}}\)\(=\frac{\left | A_1B_2+B_1B_2+C_1C_2 \right |}{\sqrt{A^2_1+B_1^2+C^2_1} .\sqrt{A^2_2+B_2^2+C^2_2}}\)

Chú ý:

• \(0^0\leq (\widehat{P,Q})\leq 90^0\).
• \((P)\perp (Q)\Leftrightarrow \vec{n}_P.\vec{n}_Q\)\(\Leftrightarrow A_1A_2+B_1B_2+C_1C_2=0\).

Ví dụ 1:

Cho ba điểm A(2;0;0), B(0;3;1), C(-1;4;2).

a) Chứng minh: A,B,C là 3 đỉnh của một tam giác

b) Tính diện tích tam giác ABC.

c) Tính độ dài đường cao kẻ từ đỉnh A của tam giác ABC.

Lời giải:

a) Ta có \(\overrightarrow {AB} ( - 2;3;1),\overrightarrow {AC} ( - 3;4;2) \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = (2;1;1) \ne \overrightarrow 0\) nên \(\overrightarrow {AB} ,\overrightarrow {AC}\) không cùng phương do đó A, B, C tạo thành 3 đỉnh của tam giác.

b) \({S_{ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right| = \frac{{\sqrt 6 }}{2}\).

 

c) \(AH = \frac{{2{S_{\Delta ABC}}}}{{BC}} = \frac{{\sqrt 6 }}{{\sqrt {{1^2} + {{(4 - 3)}^2} + {{(2 - 1)}^2}} }} = \sqrt 2\).

Ví dụ 2: 

Cho 4 điểm: A(1;0;1), B(-1;1;2), C(-1;1;0), D(2;-1;-2)

a) Chứng minh rằng: A,B,C,D là 4 đỉnh của một tứ diện.

c) Tính độ dài đường cao AH của tứ diện ABCD.

Lời giải:

a) Ta có: \(\overrightarrow {AB} = \left( { - 2;1;1} \right);\) \(\overrightarrow {AC} = \left( { - 2;1; - 1} \right)\,;\,\overrightarrow {AD} = \left( {1; - 1; - 3} \right).\)

 \(\left[ {\overrightarrow {AC} ;\overrightarrow {AC} } \right].\overrightarrow {AD} = 2 \ne 0.\)

Vậy 4 điểm A,B,C,D không đồng phẳng.

Suy ra A,B,C,D là 4 đỉnh của một tứ diện.

b) \({V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right]\overrightarrow {AD} } \right| = \frac{1}{3}\) 

Mà: \({V_{ABCD}} = \frac{1}{3}.{S_{BCD}}.AH \Rightarrow AH = \frac{1}{{{S_{BCD}}}}.\)   

\(\left[ {\overrightarrow {BC} ;\overrightarrow {CD} } \right] = \left( { - 4; - 6;0} \right) \Rightarrow {S_{BCD}} = \frac{1}{2}\left| {\left[ {\overrightarrow {BC} ;\overrightarrow {CD} } \right]} \right| = \sqrt {13} .\)

Vậy: \(AH = \frac{1}{{\sqrt {13} }}.\)   

2. Phương trình mặt phẳng và các dạng toán liên quan

Ví dụ 3: 

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) trong các trường hợp sau:

a) (P) đi qua điểm \({M_0}( - 2;3;1)\) và vuông góc với đường thẳng AB với \(A(3;1; - 2):B(4; - 3;1).\)

b) (P) đi qua điểm \({M_0}( - 2;3;1)\) và song song với mặt phẳng (Q): \(4x - 2y + 3z - 5 = 0.\)  

c) (P) đi qua điểm \({M_0}( - 2;3;1)\) và vuông góc với hai mặt phẳng (Q): x-3y+2z-1=0; (R): 2x+y-z-1=0.

d) (P) đi qua 3 điểm \(A(2;0; - 1);B(1; - 2;3);C(0;1;2).\)

Lời giải:

a) Mặt phẳng (P) có VTPT \(\overrightarrow n = \overrightarrow {AB} = (1; - 4;3).\)

• Cách 1: Do (P) đi qua \({M_0}( - 2;3;1)\) nên có phương trình là:

\(1(x + 2) - 4(y - 3) + 3(z - 1) = 0\)\(\Leftrightarrow (P):x - 4y + 3z + 11 = 0.\)  

• Cách 2: Mặt phẳng (P) có VTPT \(\overrightarrow n = \overrightarrow {AB} = (1; - 4;3)\) nên phương trình có dạng: \(x - 4y + 3z + D = 0.\)

Mặt khác: \({M_0}( - 2;3;1) \in (P) \Rightarrow D = 11\). Suy ra: \((P):x - 4y + 3z + 11 = 0.\)

b)

• Cách 1: (P)//(Q)\(\Rightarrow VTPT\overrightarrow {{n_(}_{P)}} = VTPT{\overrightarrow n _{(Q)}} = (4; - 2;3).\) 

\((P):4(x + 2) - 2(y - 3) + 3(z - 1) = 0 \Leftrightarrow (P):4x - 2y + 3z + 11 = 0.\)

• Cách 2: (P)//(Q)\(\Rightarrow (P):{\rm{4x - 2}}y + 3z + D = 0(D \ne - 5).\)

\({M_0}( - 2;3;1)\in(P)\Rightarrow D=11\Rightarrow (P):{\rm{4x - 2}}y + 3z + 11 = 0.\)

c) 

Ta có: \({\left. {\begin{array}{*{20}{l}} {(P) \bot (Q) \Rightarrow VTPT\overrightarrow {{n_{(P)}}} \bot VTPT\overrightarrow {{n_{(Q)}}} = (1; - 3;2)}\\ {(P) \bot (Q) \Rightarrow VTPT\overrightarrow {{n_{(P)}}} \bot VTPT\overrightarrow {{n_{(R)}}} = (2;1; - 1)} \end{array}} \right\}}\)

Suy ra mặt phẳng (P) có VTPT là: \({\overrightarrow {{n_{(P)}}} = \left[ {\overrightarrow {{n_{(Q)}}} ,\overrightarrow {{n_{(R)}}} } \right] = (1;5;7)}.\)

Mặt khác (P) đi qua \({M_0}( - 2;3;1)\) nên có phương trình là:

\((P):(x + 2) + 5(y - 3) + 7(z - 1) = 0 \Leftrightarrow (P):z + 5y + 7z - 20 = 0.\)

d) Cặp VTCP mặt phẳng (P) là:

\(\left\{ \begin{array}{l} \overrightarrow {AB} = ( - 1; - 2;4)\\ \overrightarrow {AC} = ( - 2;1;3) \end{array} \right. \Rightarrow VTPT\overrightarrow {{n_{(P)}}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = ( - 10; - 5; - 5).\)

Mặt khác (P) đi qua A(2;0;-1) nên có phương trình là:

 \((P): - 10(x - 2) - 5(y - 0) - 5(z + 1) = 0 \Leftrightarrow (P):2x + y + z - 3 = 0.\)

Ví dụ 4:

Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình sau:

a) 2x-3y+4z-4=0 và 3x-y-x-1=0.

b) -x+y-z+4=0 và 2x-2y+2z-7=0.

c) 3x+3y-6z-12=0 và 4x+4y-8z-16=0.

Lời giải:

a) Ta có: \(\frac{2}{3} \ne \frac{{ - 3}}{{ - 1}} \ne \frac{4}{1}\) vậy hai mặt phẳng cắt nhau.

b) Ta có: \(\frac{{ - 1}}{2} = \frac{1}{{ - 2}} = \frac{{ - 1}}{2} \ne \frac{4}{7}\) vậy hai mặt phẳng song song.

c) Ta có: \(\frac{3}{4} = \frac{3}{4} = \frac{{ - 6}}{{ - 8}} = \frac{{ - 12}}{{ - 16}}\) vậy hai mặt phẳng trùng nhau.

Ví dụ 5:

Cho hai mặt phẳng có phương trình lần lượt là: \(\left( {{m^2} - 5} \right)x - 2y + mz + m - 5 = 0\) và \(x + 2y - 3nz + 3 = 0.\)  

Tìm m và n để hai mặt phẳng trùng nhau.

Lời giải:

Hai mặt phẳng trùng nhau khi và chỉ khi:

\(\begin{array}{l} \frac{{{m^2} - 5}}{1} = \frac{{ - 2}}{2} = \frac{m}{{ - 3n}} = \frac{{m - 5}}{3}\\ \Leftrightarrow \left\{ \begin{array}{l} {m^2} - 5 = - 1\\ m = 3n\\ m - 5 = - 3 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} m = \pm 2\\ n = \frac{m}{3}\\ m = 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m = 2\\ n = \frac{2}{3} \end{array} \right. \end{array}\)

Vậy với m=2; \(n=\frac{2}{3}\) thì hai mặt phẳng trùng nhau.

Ví dụ 6:

Tìm khoảng cách từ các điểm \({M_0}\left( {1; - 1;2} \right);\,{M_1}\left( {3;4;1} \right);\,{M_2}\left( { - 1;4;3} \right)\) đến mặt phẳng x+2y+2z-10=0.

Lời giải:

\(\begin{array}{l} d\left( {{M_0},(P)} \right) = \frac{{\left| {1 + 2.( - 1) + 2.2 - 10} \right|}}{{\sqrt {{1^2} + 2{}^2 + {2^2}} }} = \frac{7}{3}\\ d\left( {{M_1},(P)} \right) = \frac{{\left| {3 + 2.4 + 2.1 - 10} \right|}}{{\sqrt {{1^2} + 2{}^2 + {2^2}} }} = 1\\ d\left( {{M_2},(P)} \right) = \frac{{\left| { - 1 + 2.4 + 2.3 - 10} \right|}}{{\sqrt {{1^2} + 2{}^2 + {2^2}} }} = 1 \end{array}\)

Ví dụ 7: 

Trên trục Oy tìm các điểm cách đều hai mặt phẳng \((P):x + y - z + 1 = 0\) và \((Q):z - y + z - 5 = 0.\)  

Lời giải:

Gọi \({M_0}\left( {{x_0};{y_0};{z_0}} \right) \in Oy.\) 

Ta có:

\(\begin{array}{l} d({M_0},(P)) = d\left( {{M_0},(Q)} \right)\\ \Leftrightarrow \frac{{\left| {{y_0} + 1} \right|}}{{\sqrt {{1^2} + {1^2} + {{( - 1)}^2}} }} = \frac{{\left| { - {y_0} - 5} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }}\\ \Leftrightarrow \left| {{y_0} + 1} \right| = \left| { - {y_0} - 5} \right|\\ \Leftrightarrow \left[ \begin{array}{l} {y_0} + 1 = {y_0} + 5\,(VN)\\ {y_0} + 1 = - {y_0} - 5 \end{array} \right. \Leftrightarrow {y_0} = - 3 \end{array}\)

Vậy M(0;-3;0).

Ví dụ 8: 

Tính góc tạo bởi mặt phẳng (P): 3x+y+4z+2017=0 và mặt phẳng (Q) chứa 3 điểm A(1;1;1); B(2;3;0); C(3;4;-1).

Lời giải:

VTPT của (P) là: \(\overrightarrow {{n_P}} = \left( {3;1;4} \right).\)   

(Q) chứa 3 điểm A(1;1;1); B(2;3;0); C(3;4;-1) nên VTPT của (Q) là:

\(\overrightarrow {{n_Q}} = \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = (6; - 5; - 4).\)

Gọi \(\alpha\) là góc giữa hai mặt phẳng (P) và (Q) ta có:

\(\begin{array}{l} \cos \alpha = \frac{{\left| {\overrightarrow {{n_P}} .\overrightarrow {{n_Q}} } \right|}}{{\left| {\overrightarrow {{n_P}} } \right|\left| {\overrightarrow {{n_Q}} } \right|}} = \frac{{\left| {3.6 + 1.( - 5) + 4.( - 4)} \right|}}{{\sqrt {{3^2} + {1^2} + {4^2}} .\sqrt {{6^2} + {{( - 5)}^2} + {{( - 4)}^2}} }} = \frac{3}{{\sqrt {2002} }}\\ \Rightarrow \alpha \approx {86^0}9'. \end{array}\)

Nội dung bài học sẽ giới thiệu đến các em dạng của phương trình mặt phẳng, cách xác định vectơ pháp tuyến của một mặt phẳng. Bên cạnh đó là các công thức tính góc giữa hai mặt phẳng, khoảng cách từ một điểm đến mặt phẳng, phương pháp xác định vị trí tương đối của mặt phẳng. Ngoài ra trong bài học này các em còn được tìm hiểu khái niệm hoàn toàn mới là tích có hướng giữa hai vectơ và những ứng dụng. 

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 12 Bài 2 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Trong không gian với hệ tọa độ Oxyz cho \(A(1;2;0),B(3;-1;1)\) và \(C(1;1;1)\). Tính diện tích S của tam giác ABC.

  • A.  \(S=1\) 
  • B.  \(S=\frac{1}{2}\) 
  • C.  \(S=\sqrt{3}\) 
  • D.  \(S=\sqrt{2}\)

• Câu 2:

  Trong không gian Oxyz, cho các điểm \(A\left( {1;2;3} \right);B\left( {0;0;2} \right);C\left( {1;0;0} \right);D\left( {0; - 1;0} \right)\). Tính thể tích khối tứ diện ABCD.

  • A. 1
  • B.  \(\frac{1}{6}\)
  • C.  \(\frac{1}{3}\)
  • D. \(\frac{1}{2}\)

• Câu 3:

  Trong không gian với hệ trục Oxyz, viết phương trình mặt phẳng đi qua điểm A(1;3;-2) và song song với mặt phẳng  \(\left( P \right):2x - y + 3z + 4 = 0\).​

  • A.  2x - y + 3z + 7 = 0 
  • B.  2x + y - 3z + 7 = 0  
  • C. 2x + y + 3z + 7 = 0  
  • D.  2x - y + 3z - 7 = 0  

• Câu 4:

  Trong không gian với hệ trục Oxyz, viết phương trình mặt phẳng chứa hai điểm A(1;0;1), B(-1;2;2) và song song với trục Ox.

  • A. x + y - z = 0  
  • B. 2y - z + 1 = 0  
  • C. y - 2z + 2 = 0  
  • D. x + 2z - 3 = 0  

• Câu 5:

  Trong không gian với hệ tọa độ Oxyz cho G(1;2;3). Viết phương trình mặt phẳng (P) đi qua điểm G và cắt các trục tọa độ tại ba điểm phân biệt A, B, C sao cho G là trọng tâm của tam giác ABC.​

  • A.  \(\left( P \right):\frac{x}{3} + \frac{y}{6} + \frac{z}{9} = 1\)
  • B. \(\left( P \right):x + \frac{y}{2} + \frac{z}{3} = 3\)
  • C.  \(\left( P \right):x + y + z - 6 = 0\) 
  • D. \(\left( P \right):x + 2y + 3{\rm{z}} - 14 = 0\)

• Câu 6:

  Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A(1;1;1)\) và \(B(1;3;-5)\) Viết phương trình mặt phẳng trung trực của AB.

  • A.  \(y - 3z + 4 = 0\)
       
  • B.  \(y - 3z - 8 = 0\)
  • C.  \(y - 2z -6 = 0\)  
  • D.  \(y - 2z + 2 = 0\)

• Câu 7:

  Trong không gian Oxyz, cho mặt cầu  \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 2 = 0\) và mặt phẳng \(\left( \alpha \right):4x + 3y - 12z + 10 = 0\). Viết phương trình mặt phẳng tiếp xúc với (S) và song song \((\alpha )\).​​

  • A. \(4x + 3y - 12z + 78 = 0\)
  • B.  \(4x + 3y - 12z + 26 = 0\) hoặc \(4x + 3y - 12z - 78 = 0\)
  • C.  \(4x + 3y - 12z - 26 = 0\) 
  • D.  \(4x + 3y - 12z - 26 = 0\) hoặc \(4x + 3y - 12z + 78 = 0\)

• Câu 8:

  Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( \alpha \right):2x + my + 3z - 5 = 0\) và \(\left( \beta \right):nx - 8y - 6z + 2 = 0\left( {m,n \in \mathbb{R} } \right)\) . Tìm giá trị của m và n để hai mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau?

  • A.  \(n=m=-4\) 
  • B.  \(n=-4; m=4\)
  • C.  \(n=m=4\) 
  • D. \(n=4;m=-4\)

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 12 Bài 2 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Hình học 12 Cơ bản và Nâng cao.

Bài tập 3.28 trang 114 SBT Hình học 12

Bài tập 3.29 trang 114 SBT Hình học 12

Bài tập 3.30 trang 114 SBT Hình học 12

Bài tập 15 trang 89 SGK Hình học 12 NC

Bài tập 16 trang 89 SGK Hình học 12 NC

Bài tập 17 trang 89 SGK Hình học 12 NC

Bài tập 18 trang 90 SGK Hình học 12 NC

Bài tập 19 trang 90 SGK Hình học 12 NC

Bài tập 20 trang 90 SGK Hình học 12 NC

Bài tập 21 trang 90 SGK Hình học 12 NC

Bài tập 22 trang 90 SGK Hình học 12 NC

Bài tập 23 trang 90 SGK Hình học 12 NC

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.