Bài 1 trang 71 SGK Hình học 11
Tóm tắt bài
Đề bài
Trong mặt phẳng (\( \alpha\)) cho hình bình hành \(ABCD\). Qua \(A, B, C, D\) lần lượt vẽ bốn đường thẳng \(a,b,c,d\) song song với nhau và không nằm trên (\( \alpha\)). Trên \(a, b, c\) lần lượt lấy ba điểm \(A', B', C'\) tùy ý
a) Hãy xác định giao điểm \(D'\) của đường thẳng \(d\) với mặt phẳng \((A'B'C')\).
b) Chứng minh \(A'B'C'D'\) là hình bình hành.
Hướng dẫn giải
a) Xác định điểm chung của d và \((A'B'C')\).
b) Sử dụng nội dung của định lí 3: Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết
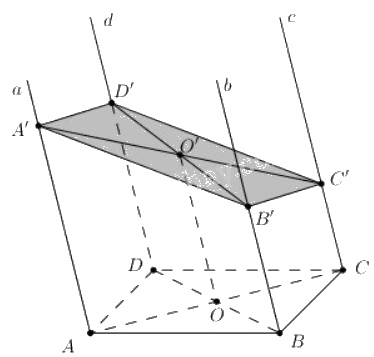
a) Gọi \(O = AC ∩ BD\); \(O'\) là trung điểm \(A'C'\) thì OO' là đường trung bình của hình thang \(ACC'A'\) \(\Rightarrow OO' // AA'\)
\(\Rightarrow OO'// d // b\) mà \(OO' \subset mp (b;d) \Rightarrow O' \in mp (b;d) \) ( mặt phẳng xác định bởi hai đường thẳng song song).
Trong \(mp (b;d)\), gọi \(D'=d ∩ B'O'\) ta có:
\(\left\{ \begin{array}{l}D' \in B'O \subset \left( {ABC} \right)\\D' \in d\end{array} \right. \Rightarrow D' = d \cap \left( {ABC} \right)\) chính là điểm cần tìm.
b) \(mp(a;d) // mp( b;c)\) , mặt phẳng thứ 3 \((A'B'C'D')\) cắt hai mặt phẳng trên theo hai giao tuyến song song : \(A'D' // B'C'\). Chứng minh tương tự được \(A'B' // D'C'\). Từ đó suy ra \(A'B'C'D'\) là hình bình hành.
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 11
Lớp 11 - Năm thứ hai ở cấp trung học phổ thông, gần đến năm cuối cấp nên học tập là nhiệm vụ quan trọng nhất. Nghe nhiều đến định hướng sau này rồi học đại học. Ôi nhiều lúc thật là sợ, hoang mang nhưng các em hãy tự tin và tìm dần điều mà mình muốn là trong tương lai nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
