Đường thẳng và mặt phẳng song song trong không gian
Tóm tắt bài
Đường thẳng và mặt phẳng song song trong không gian
Hôm nay sẽ chia sẻ với các bạn về nội dung đường thẳng và mặt phẳng song song lý thuyết kết hợp với bài tập vận dụng!
I. Lý thuyết chung?
1. Vị trí tương đối của đường thẳng và mặt phẳng.
Đường thẳng và mặt phẳng song song khi nào?
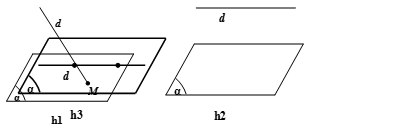
Cho đường thẳng d và mặt phẳng (α), ta có ba vị trí tương đối giữa chúng là:
– d và (α) cắt nhau tại điểm M, kí hiệu {M} = d ∩ (α) hoặc để đơn giản ta kí hiệu {M} = d ∩ (α) (h1)
– d song song với (α), kí hiệu d // (α) hoặc (α) // d( h2)
– d nằm trong (α), kí hiệu d ⊂ (α) (h3)
2. Các định lí và tính chất.
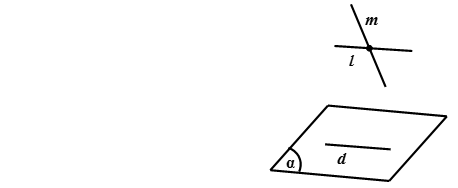
- Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d’ nằm trong (α) thì d song song với (α).
Vậy \(\begin{align} \begin{cases} d\notin(\alpha) \\ d//d' \\d'\in(\alpha) \end{cases}\end{align}\)\(\Rightarrow d//(\alpha)\)
- Để thỏa mãn một đường thẳng d song song với mặt phẳng xác định (α). Bên cạnh đó, một mặt phẳng bất kỳ khác là (β) sao cho d nằm trên mặt phẳng đó và giao với (α) theo điều kiện giao tuyến d’ thì d’ // d.
Vậy \(\begin{align} \begin{cases} d\in(\alpha) \\ d\in(\beta) \\(\alpha)\cap(\beta) \end{cases}\end{align}\)\(\Rightarrow d//d'\)
- Trong trường hợp một đường thẳng cùng song song với hai mặt phẳng phân biệt đồng thời thì ta có định lý rằng giao tuyến giữa hai đường nếu có sẽ song song với đường thẳng ban đầu.
Vậy \(\begin{align} \begin{cases} (\alpha) //d\\ (\beta)//d \\(\alpha)\cap(\beta) \end{cases}\end{align}\)\(\Rightarrow d//d'\)
- Đối với trường hợp hai đường thẳng chéo nhau ta luôn có chỉ một và duy nhất một mặt phẳng có chứa một đường thẳng bất kỳ nào đó song song với đường thẳng được xem xét.
Giải bài tập về đường thẳng, mặt phẳng song song
II. Các dạng bài tập
1. Dạng 1: Chứng minh đường thẳng song song với mặt phẳng
Phương pháp: Cách để chứng minh đường song song với mặt ta áp dụng cách chứng minh sau: Xét đường thẳng d song song với mặt phẳng (α) khi và chỉ khi chứng minh được d song song với một đường thẳng d' sao cho d' nằm trong mặt phẳng (α).
Ví dụ: Xét hình S.ABCD với mặt phẳng đáy là ABCD, biết rằng đáy đã cho ở dạng hình bình hành. Trên tam giác SAB xác định trọng tâm G và trên AB ta lấy trung điểm là điểm I và xác định điểm M bất kỳ thỏa mãn điều kiện \(AM=\dfrac{1}{3}AD\).
a) Ta xác định qua điểm M một đường thẳng bất kỳ thỏa mãn điều kiện đầu bài song song với AB và giao với cạnh Ci Tại M. CMR NG // (SCD).
b) CMR MG//(SCD).
Lời giải:
a) Ta có \(\dfrac{IN}{IC}=\dfrac{BJ}{BC}=\dfrac{AM}{AD}=\dfrac{1}{3},\dfrac{IG}{IS}=\dfrac{1}{3} \Rightarrow \dfrac{IN}{IC}=\dfrac{IG}{IS}\Rightarrow NG//SC\)
Mà \(SC \in (SCD) \Rightarrow NG//(SCD)\).
b) Gọi E là giao điểm của IM và CD.
Ta có \(\dfrac{IM}{IE}=\dfrac{AM}{AD}=\dfrac{1}{3}\Rightarrow \dfrac{IM}{IE}=\dfrac{IG}{IS}\Rightarrow MG//SE, SE\in (SCD)\Rightarrow GM//(SCD)\).
2. Dạng 2: Dựng thiết bị song song với đường thẳng
Phương pháp: Sử dụng định nghĩa và các tính chất hoặc biểu thức tọa độ của phép tịnh tiến. Trong phần này ta sẽ xét thiết diện cùa mặt phẳng (α) đi qua một điểm song song với hai đường thẳng chéo nhau hoặc (α) chứa một đường thẳng song song với một đường thẳng, để xác định thiết diện loại này ta sử dụng tính chất:
\(\begin{align} \begin{cases} (\alpha)//d \\ d\in(\beta) \\ M\in (\alpha)\cap (\beta) \end{cases}\end{align}\)\(\Rightarrow (\alpha)\cap (\beta)=d'//d,M\in d'\).
Ví dụ: Xét hình S.ABCD với mặt phẳng đáy là ABCD, lần lượt lấy hai điểm M và N sao cho hai điểm đó nằm trên hai đoạn thẳng AB và CD, xác định một mặt phẳng (α) bất kỳ giao với đoạn MN và song song với SA.
a) Thiết diện của hình chop S.ABCD là hình nào? Xác định?
b) dể đáy của thiết diện là một hình thang ta cần điều kiện gì ở đoạn MN.
Lời giải:
Ta có \(\begin{align} \begin{cases} M\in (\alpha) \cap (SAB) \\ (\alpha) //SA \\ SA\in (SAB) \end{cases}\end{align}\)
\(\Rightarrow (SAB) \cap (\alpha) =MQ//SA,Q\in SB.\)
Trong (ABCD) gọi \(I=AC\cap MN\)
\(\begin{align} \begin{cases} I\in MN\in (\alpha) \\ I\in AC\in(SAC) \end{cases}\end{align}\) \(\Rightarrow I\in (\alpha)\cap(SAC)\)
Vậy \(\begin{align} \begin{cases} I\in(SAC)\cap(\alpha)\\ (\alpha)//SA \\ SA\in(SAC) \end{cases}\end{align}\)
\(\Rightarrow (SAC)\cap(\alpha)=IP//SA,P\in SC\)
Từ đó ta có \((\alpha)\cap (SBC)=PQ(\alpha)\cap(SAD)=NP\)
Thiết diện cần tidm là tứ giác MNPQ.
b) Tứ giác MNPQ là một hình thang khi MN//PQ hoặc MQ//NP.
TH1:
Nếu MQ//NP thì ta có \(\begin{align} \begin{cases} MQ//NP \\ MQ//SA \end{cases}\end{align}\)
Quy ra SA//NP.
Mà NP thuộc (SCD) suy ra SA//(SCD) (điều này vô lý).
TH2:
Để khiến cho MN//PQ ta lần lượt xét ba mặt phẳng sau: (ABCD), (α), (SBC), lần lượt tìm điểm giao của hai mặt phẳng một lần lượt là MN, BC, PQ nên MN//BC.
Đảo lại nếu MN//BC thì \(\begin{align} \begin{cases} MN\in (\alpha) \\ BC\in(SBC)\\ PQ=(\alpha)\cap(SBC) \end{cases}\end{align}\)
Suy ra MN//PQ nên tứ giác MNPQ là hình thang.
Vậy để tứ giác MNPQ là hình thang thì điều kiện là MN//BC.
Hy vọng với những kiến thức bổ ích mà muốn chia sẻ về cách giải đường thẳng và mặt phẳng song song trên đây, sẽ giúp các bạn học tốt hơn môn Toán học!
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 11
Lớp 11 - Năm thứ hai ở cấp trung học phổ thông, gần đến năm cuối cấp nên học tập là nhiệm vụ quan trọng nhất. Nghe nhiều đến định hướng sau này rồi học đại học. Ôi nhiều lúc thật là sợ, hoang mang nhưng các em hãy tự tin và tìm dần điều mà mình muốn là trong tương lai nhé!
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
