Bài 6 trang 27 (Hệ trục tọa độ) SGK Hình học 10
Tóm tắt bài
Đề bài
Cho hình bình hành \(ABCD\) có \(A(-1; -2), B(3;2), C(4;-1)\). Tìm tọa độ điểm \(D.\)
Hướng dẫn giải
Dựa vào tính chất của hình bình hành và khái niệm hai vecto bằng nhau để làm bài.
Lời giải chi tiết
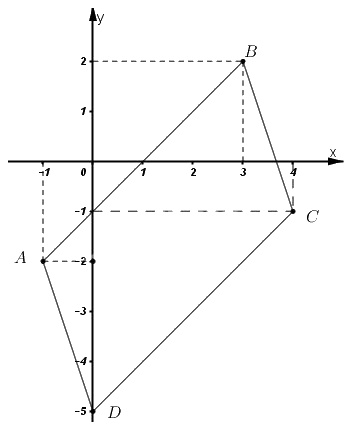
Tứ giác \(ABCD\) là hình bình hành nên
\(\overrightarrow{CD}=\overrightarrow{BA}\)
Gọi \((x; y)\) là tọa độ của \(D\) thì
\(\overrightarrow{CD} = (x-4; y+1)\)
\(\overrightarrow{BA}= (-4;-4)\)
\(\overrightarrow{CD}\) = \(\overrightarrow{BA}\) ⇔ \(\left\{\begin{matrix} x-4 = -4\\ y+1 = -4 \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} x=0\\ y=-5 \end{matrix}\right.\)
Vậy điểm \(D(0;-5)\) là điểm cần tìm.
Bạn có biết?
Toán học là ngành nghiên cứu trừu tượng về những chủ đề như: lượng (các con số), cấu trúc, không gian, và sự thay đổi.Các nhà toán học và triết học có nhiều quan điểm khác nhau về định nghĩa và phạm vi của toán học
Nguồn : Wikipedia - Bách khoa toàn thưTâm sự Lớp 10
Lớp 10 - Năm thứ nhất ở cấp trung học phổ thông, năm đầu tiên nên có nhiều bạn bè mới đến từ những nơi xa hơn vì ngôi trường mới lại mỗi lúc lại xa nhà mình hơn. Được biết bên ngoài kia là một thế giới mới to và nhiều điều thú vị, một trang mới đang chò đợi chúng ta.
Nguồn : ADMIN :))Copyright © 2021 HOCTAPSGK
