Tổng hợp kiến thức và các dạng bài tập hình học lớp 4 là tài liệu nhằm giúp quý thầy cô và quý phụ huynh hướng dẫn các em học sinh nắm chắc các dạng bài tập hình học trong chương trình học lớp 4. Thông qua bộ tài liệu này sẽ giúp cho các em học sinh ôn tập, củng cố Toán học lớp 4 một cách bài bản và chi tiết nhất. Sau đây, mời quý phụ huynh cùng quý thầy cô và các em học sinh tải về tài liệu.

Phần 1: Kiến thức cần nhớ

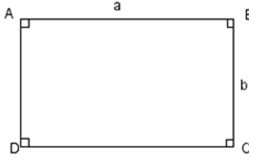
1. Hình chữ nhật: Hình chữ nhật là hình tứ giác có 4 góc vuông, 2 cạnh dài bằng nhau và 2 cạnh ngắn bằng

Chu vi: 𝑷 = (𝒂 + 𝒃) × 𝟐 (cùng số đo).

Diện tích: 𝑺 = 𝒂 × 𝒃 (cùng số đo).

Chú ý:

• Hình vuông là hình chữ nhật đặc biệt (có 4 cạnh bằng nhau).
• Chu vi hình chữ nhật là 1 số chia hết cho 2 nếu chiều dài và chiều rộng là các số tự nhiên.
• Nếu tăng chiều dài của hình chữ nhật lên a đơn vị thì chu vi sẽ tăng lên a x 2 đơn vị (vì có 2 chiều dài)
• Nếu tăng chiều rộng của hình chữ nhật lên a đơn vị thì chu vi sẽ tăng lên a x 2 đơn vị (vì có 2 chiều rộng)
• Nếu giảm chiều dài của hình chữ nhật lên a đơn vị thì chu vi sẽ giảm lên a x 2 đơn vị (vì có 2 chiều dài)
• Nếu giảm chiều rộng của hình chữ nhật lên a đơn vị thì chu vi sẽ giảm lên a x 2 đơn vị (vì có 2 chiều rộng)
• Nếu gấp một chiều của một hình chữ nhật lên bao nhiêu lần thì diện tích sẽ tăng lên bấy nhiêu lần.
• Nếu giảm một chiều của một hình chữ nhật đi bao nhiêu lần thì diện tích sẽ giảm đi bấy nhiêu lần.
• Nếu tăng hay giảm cả hai chiều thì diện tích sẽ tăng hay giảm đi tích hai số lần đó.

2. Hình vuông: Hình vuông là hình tứ giác có 4 góc vuông và 4 cạnh bằng

Chu vi: 𝑷 = 𝒂 × 𝟐 (cùng số đo)

Diện tích: 𝑺 = 𝒂 × 𝒂 (cùng số đo).

Chú ý:

- Trong hình vuông nếu tăng 1 cạnh lên a đơn vị thì chu vi sẽ tăng 4 x a đơn vị.

- Trong hình vuông nếu cạnh tăng lên a lần thì diện tích sẽ tăng lên a x a lần.

- Chu vi hình vuông là một số chia hết cho 4 nếu cạnh hình vuông là số tự nhiên.

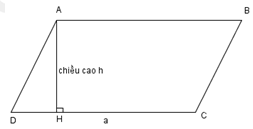
3. Hình bình hành: Hình bình hành là tứ giác có 2 cặp cạnh đối diện song song và bằng

Hình bình hành có 1 góc vuông là trường hợp đặc biệt của hình chữ nhật.

Diện tích: 𝑺 = 𝒂 × 𝒉 (cùng số đo).

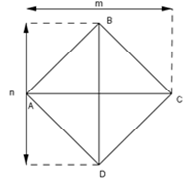
4. Hình thoi: Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và có 4 cạnh bằng

Diện tích: 𝑺 = 1/2 (m x n ) (cùng số đo).

Phần 2: Các dạng toán

I - Dạng 1: Toán về nhận biết hình

Thường gặp hai loại như sau:

• Loại 1: Đọc tên các hình có được trên một hình vẽ cho trước.

Loại này không khó nhưng các em thường mắc những sai lầm là liệt kê các hình còn thiếu hoặc trùng lặp. Để khắc phục ta phải đọc theo một thứ tự thật khoa học, như:

- Đọc hết các đoạn thẳng theo yêu cầu của đề mà các hình này có chung đỉnh theo thứ tự lần lượt đến khi hết các đỉnh còn lại.

- Các hình bé được phân chia trên hình cho trước ta lần lượt ghi mỗi hình bé bằng một con số 1; 2; 3; … Đọc tên những hình theo yêu cầu của đề mà chỉ gồm hình ghi 1 số (1 hình bé) có thể được, tiếp tục đọc tên những hình ghép bởi 2 hình bé rồi 3 hình bé và cứ thế…

Khi đọc lưu ý các hình lặp lại chỉ đọc 1 lần.

• Loại 2: Tính số hình có được trong trường hợp hình có trước có số lượng đỉnh (điểm) rất lớn, tổng quát. Ta nên thực hiện theo hai bước:

- Bước 1: Tính số hình có được theo yêu cầu đề toán ở trường hợp đơn giản(xét vài trường hợp).

- Bước 2: Tìm ra quy luật của số hình (dựa vào quy luật của dãy số). Từ đó dựa vào quy tắc và công thức để tính.

CÁC BÀI TẬP CỤ THỂ:

Bài 1: Cho hình vẽ bên: Hình có 8 cạnh, nối 2 đỉnh không cùng thuộc một cạnh thì được một đường chéo. Hỏi có bao nhiêu đường chéo?

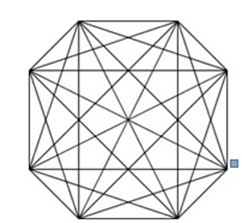
Bài giải:

Cách 1: Hình đã cho có 8 đỉnh, vậy có 8 cách chọn điểm thứ nhất, sau khi chọn điểm thứ nhất ta còn 7 đỉnh nên có 7 cách chọn điểm thứ 2 để nối với điểm thứ nhất được một đoạn thẳng.

Mỗi cách chọn ta được 1 đoạn thẳng như vậy có 7 × 8 = 56 đoạn thẳng, nhưng như vậy mỗi đoạn thẳng đã tính 2 lần, do đó số đoạn thẳng thực tế là 56: 2 = 28 đoạn thẳng.

Vì hình có 8 cạnh nên số đường chéo trong hình là: 28 − 8 = 20 (đường chéo).

Cách 2: Qua mỗi đỉnh của hình ta vẽ được 8 - 3 = 5 (đường chéo)

Có 8 đỉnh nên vẽ được 8 × 5 = 40 (đường chéo)

Nhưng mỗi đường chéo được tính 2 lần, vậy số được chéo vẽ được là: 40: 2 = 20 (đường chéo).

Có thể rút ra công thức tổng quát cho dạng này là 𝒏 × (𝒏 − 𝟑): 𝟐 với 𝒏 là số tự nhiên và 𝒏 > 𝟑.

Bài 2: Cho tứ giác ABCD như hình vẽ. Hãy kẻ thêm 2 đoạn thẳng để được 6 hình tứ giác.

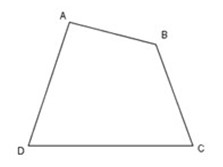
Bài giải

Có thể vẽ như hình bên. Khi đó 6 hình tứ giác là: AEGD; AHKD; ABCD; EHKG; EBCG; HBCK.

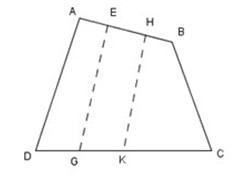
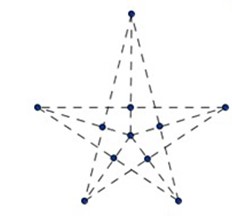
Bài 3: Hãy trồng 11 cây thành 10 hàng mỗi hàng 3 cây?

Bài giải

Có thể trồng theo hình vẽ bên.

Bài 4: Nối điểm chính giữa cạnh hình vuông thứ nhất ta được hình vuông thứ hai. Nối điểm chính giữa các cạnh hình vuông thứ hai ta được hình vuông thứ ba, và cứ tiếp tục như vậy….

Hãy tìm số hình tam giác có trong hình vẽ như vậy đến hình vuông thứ 100?

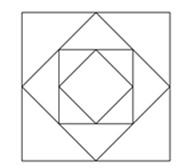
Bài giải

Theo đề bài ta có bảng sau

Số hình tam giác được tạo thành là: 4 × 99 = 396 (tam giác).

Có thể rút ra công thức tổng quát cho dạng này là 𝟒 × (𝒏 − 𝟏) 𝒗ớ𝒊 𝒏 lần vẽ thứ 𝒏.

II - Dạng 2: Toán về cắt ghép hình

Cắt hình cho trước thành nhiều hình bé rồi ghép lại thành hình khác theo yêu cầu đề toán là dạng tương đối khó, đòi hỏi học sinh phải linh hoạt, cần nhớ là quan sát thật kỹ hình dạng, kích thước của hình cho trước và hình cần ghép, số mảnh cần cắt. Từ đó dự đoán các trường hợp có thể được. Tiến hành thử chọn để tìm ra lời giải đúng.

CÁC BÀI TẬP CỤ THỂ:

Bài 1: Cho tờ giấy hình chữ nhật có chiều dài 5cm, rộng 4cm. Cắt rời từng mảnh như hình vẽ rồi ghép lại thành hình vuông?

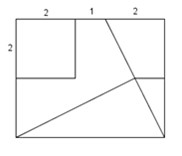
Bài giải

Cắt và ghép như hình dưới đây:

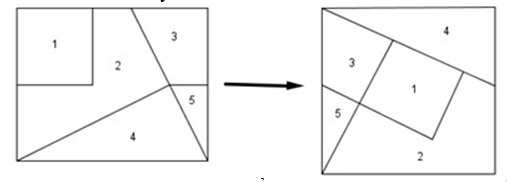
Bài 2: Cắt tờ giấy như hình bên thành 4 mảnh để ghép lại được một hình vuông?

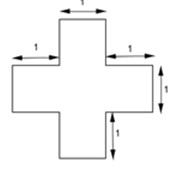
Bài giải:

Cắt và ghép như hình dưới đây:

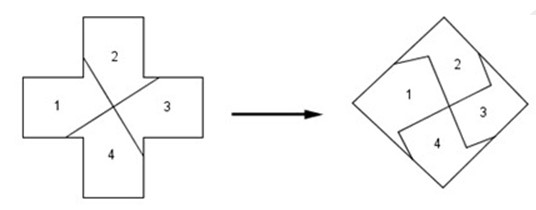
Bài 3: Cho tấm bìa bên gồm 14 hình vuông. Hỏi có thể cắt thành 7 tấm bìa nhỏ hình chữ nhật mà mỗi tấm bìa nhỏ gồm 2 ô vuông được không?

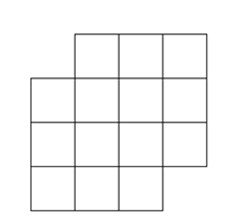
Bài giải:

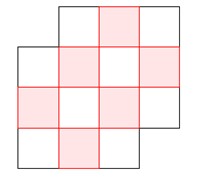
Tô màu 6 ô vuông như hình vẽ bên. Từ đó nhận thấy cứ mỗi hình chữ nhật gồm 2 ô vuông được cắt ra thì có 1 ô màu trắng và 1 ô màu. Như vậy nếu cắt tấm bìa đã cho thành 7 tấm bìa nhỏ mà mỗi tấm bìa có 2 ô vuông thì sẽ có 7 ô màu trắng và 7 ô màu. Điều này không thể xảy ra vì chỉ có 6 ô màu.

III - Dạng 3: Toán về cắt ghép toán hình (tính toán)

Đây là dạng toán thường gặp, và quan trọng, muốn đạt được điểm tối đa của bài

Toán dạng này các em cần học thuộc các công thức tính chu vi, diện tích. Vận dụng linh hoạt các công thức này trong bài toán, biết tóm tắt nội dung và khéo léo vận dụng các phương pháp giải ở tiểu học, như dùng sơ đồ đoạn thẳng, rút về đơn vị, lập tỉ số, chia tỉ lệ…để áp dụng vào từng bài đưa ra cách giải đúng, bài giải hay.

CÁC BÀI TẬP CỤ THỂ

Bài 1: Một mảnh vườn hình chữ nhật có chu vi bằng 128m. Tính diện tích của vườn biết rằng chiều rộng ngắn hơn chiều dài 8m?

Ta có sơ đồ sau:

Nửa chu vi mảnh vườn là:

128 : 2 = 64 (𝑚)

Chiều rộng mảnh vườn là: (64 − 8): 2 = 28 (𝑚)

Chiều dài mảnh vườn là: 28 + 8 = 36 (𝑚)

Diện tích mảnh vườn là:

28 × 36 = 1008 (m²).

Đáp số: 1008 m²

• Ôn tập các dạng Toán cơ bản lớp 4
• Giáo án môn Tiếng Việt lớp 4 chuẩn kiến thức kỹ năng
• Giáo án trọn bộ các môn học Lớp 4

Tài liệu vẫn còn, mời các bạn tải về để xem tiếp