Giải Toán lớp 8 Luyện tập chung bao gồm đáp án chi tiết, cùng hướng dẫn giải cho từng bài tập trong SGK Toán 8 Tập 1 Kết nối tri thức với cuộc sống trang 56.

Lời giải Toán 8 Kết nối tri thức trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 8, từ đó học tốt môn Toán lớp 8 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài Luyện tập chung trang 56 Chương III: Tứ giác. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Giải Toán 8 Kết nối tri thức Tập 1 trang 56

Bài 3.9

Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?

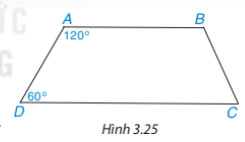
Hướng dẫn:

Vận dụng các tính chất của hình thang.

Bài giải:

Hai góc trong cùng phía A và D bù nhau nên AB // CD suy ra ABCD là hình thang

Bài 3.10

Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết , tính số đo các góc của hình thang đó.

Hướng dẫn:

Vận dụng Tổng các góc trong một tứ giác bằng 360 độ.

Vận dụng các tính chất của hình thang cân.

Bài giải:

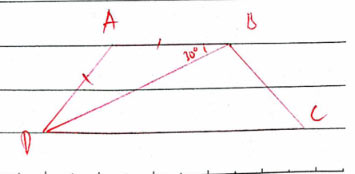
Ta có: AB = AD suy ra tam giác ABD cân tại A

Xét hình thang cân ABCD ta có:

Bài 3.11

Tính số đo các góc của tứ giác ABCD trong Hình 3.26

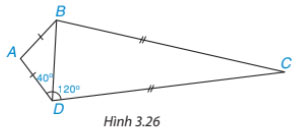
Hướng dẫn:

Vận dụng các tính chất của tam giác cân

Vận dụng định lí Tổng các góc trong một tam giác.

Bài giải:

AB = AD suy ra tam giác ABD cân tại A

CB = CD suy ra tam giác CBD cân tại C

Bài 3.12

Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R

a) Chứng minh tứ giác APMR là hình thang cân

b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC

c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?

Hướng dẫn:

Vận dụng các tính chất của tam giác đều, tính chất của hình thang cân

Bài giải:

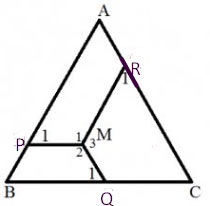
a) Ta có MR // AP suy ra APMR là hình thang

PM // BQ suy ra (hai góc đồng vị)

Lại có: (do tam giác ABC đều)

Suy ra APMR là hình thang cân

b) Tương tự câu a) ta chứng minh được tứ giác QMRC và PMQB là hình thang cân

suy ra PR = MA, RQ = MC, PQ = MB (cặp đường chéo của hình thang cân)

c) Tam giác PRQ đều khi PR = RQ = PQ hay MA = MB = MC suy ra M cách đều 3 đỉnh tam giác ABC hay chính là tâm đương tròn ngoại tiếp tam giác ABC