Toán lớp 11 tập 2 trang 25 - Chân trời sáng tạo

Toán lớp 11 tập 2 trang 19, 20, 21, 22, 23, 24, 25 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 tham khảo.

Giải Toán 11 Chân trời sáng tạo bài 3 Hàm số mũ Hàm số lôgarit được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 25. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 11 tập 2 bài 3 Hàm số mũ Hàm số lôgarit Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.

Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit

I. Toán 11 Chân trời sáng tạo bài 3 trang 25
II. Luyện tập Hàm số mũ, Hàm số lôgarit

Vẽ đồ thị các hàm số sau:

a) $y=4^{x}$

b) $y = (\frac{1}{4})^{x}$

Bài làm

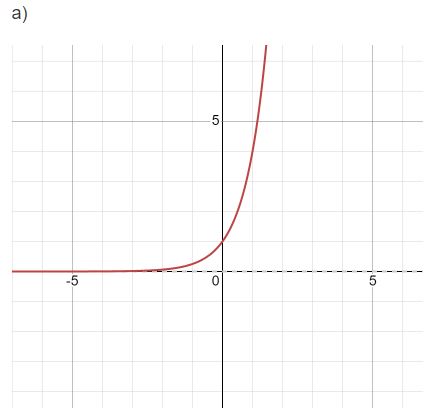
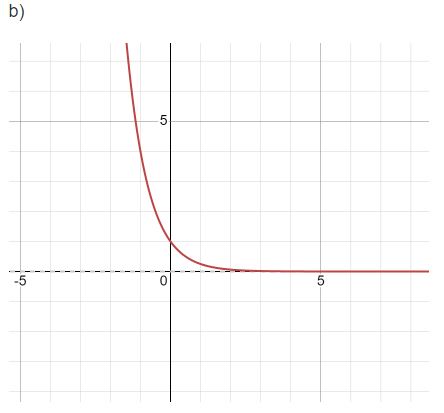
Bài 2

So sánh các cặp số sau

a) 1,3^0,7 và 1,3^0,6

b) 0,75^−2,3 và 0,75^−2,4

Bài làm

a) Vì 1,3 > 1 nên hàm số y = 1,3^x là hàm số đồng biến trên R

Mà 0,7 > 0, 6 nên 1,3^0,7 > 1,3^0,6

b) Vì 0,75 < 1 nên hàm số y = 0,75^x là hàm số nghịch biến trên R

Mà -2,3 > -2,4 nên 0,75^−2,3 > 0,75^−2,4

Bài 3

Tìm tập xác định của các hàm số:

a) log2(3 − 2x)

b) log3(x² + 4x)

Bài làm

a) $log_{2}(3-2x)$ xác định khi 3 - 2x > 0 Hay x < $\frac{3}{2}$

b) $log_{3}(x^{2}+4x)$ xác định khi $x^{2}+4x$ > 0 hay x > 0 hoặc x < -4

Bài 4

Vẽ đồ thị các hàm số

a) y = logx

b) $y=log_{\frac{1}{4}}x$

Bài làm

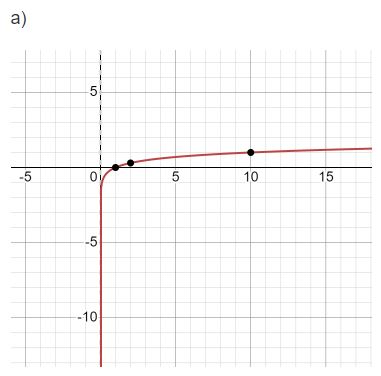
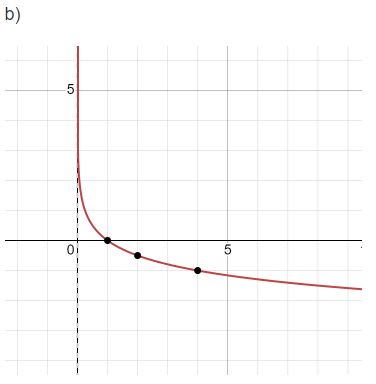
Bài 5

So sánh các cặp số sau:

a) $log_{\pi}0,8 và log_{\pi}1,2$

b) $log_{0,3}2 và log_{0,3}2,1$

Bài làm

a) Vì $\pi > 1$ nên hàm số $log_{\pi}x$ đồng biến trên $(0;+\infty)$

Mà 0,8 < 1,2 nên $log_{\pi}0,8 < log_{\pi}1,2$

b) Vì 0,3 > 1 nên hàm số $log_{0,3}x$ nghịch biến trên $(0;+\infty)$

Mà 2 < 2,1 nên $log_{0,3}2>log_{0,3}2,1$

Bài 6

Cường độ ánh sáng I dưới mặt biển giảm dần theo độ sâu theo công thức I = I₀.a^d, trong đó I₀ là cường độ ánh sáng tại mặt nước biển, a là hằng số (a > 0) và d là độ sâu tính bằng mét tính từ mặt nước biển.

a) Có thể khẳng định rằng 0 < a < 1 không? Giải thích.

b) Biết rằng cường độ ánh sáng tại độ sâu 1 m bằng 0,95I₀. Tìm giá trị của a

c) Tại độ sâu 20m, cường độ ánh sáng bằng bao nhiêu phần trăm so với I₀? (Làm tròn kết quả đến hàng đơn vị)

Bài làm

a) Vì cường độ ánh sáng giảm dần theo độ sâu, tức là hàm số I = I₀a^d nghịch biến

Do đó, 0 < a < 1

b) Khi d = 1, ta có 0,95I₀=I₀.a¹

Suy ra a = 0,95

c) Khi d = 20. Ta có I = I₀.0,95²⁰= 0,36I₀

Vậy tại độ sâu 20m thì I = 36

Bài 7

Công thức $h = -19,4log\frac{P}{P_{0}}$ là mô hình đơn giản cho phép tính độ cao h so với mặt nước biển của một vị trí trong không trung (tính bằng kilômét) theo áp suất không khí P tại điểm đó và áp suất $P_{0}$ của không khí tại mặt nước biển (cùng tính bằng $P_{a}$ - đơn vị áp suất, đọc là Pascal)

a) Nếu áp suất không khí ngoài máy bay bằng $\frac{1}{2}P_{0}$ thì máy bay đang ở độ cao nào?

b) Áp suất không khí tại đỉnh của ngọn núi A bằng $\frac{4}{5}$ lần áp suất không khí tại đỉnh của ngọn núi B. Ngọn núi nào cao hơn và cao hơn bao nhiêu kilomet? (Làm tròn kết quả đến hàng phần mười)

II. Luyện tập Hàm số mũ, Hàm số lôgarit

Bài trắc nghiệm số: 4640

Toán lớp 11 tập 2 trang 25 - Chân trời sáng tạo

Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit

Giải Toán 11 Chân trời sáng tạo trang 19, 20, 21, 22, 23, 24, 25