Giải Toán 11 Bài tập cuối chương IV là tài liệu vô cùng hữu ích giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 11 Cánh diều tập 1 trang 120, 121.
Toán 11 Cánh diều tập 1 trang 120, 121 được biên soạn đầy đủ, chi tiết trả lời các câu hỏi từ bài 1 đến bài 10 chương Đường thẳng và mặt phẳng trong không gian, quan hệ song song giúp các bạn có thêm nhiều nguồn ôn tập đối chiếu với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 tập 1 Bài tập cuối chương IV Cánh diều, mời các bạn cùng theo dõi tại đây.
Giải Toán 11 Bài tập cuối chương IV - Tập 1 Cánh diều
Toán lớp 11 Cánh diều tập 1 trang 120, 121
Bài 1 trang 120
Trong không gian, hai đường thẳng song song với nhau khi và chỉ khi:
A. Hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.
B. Hai đường thẳng không có điểm chung.
C. Hai đường thẳng cùng nằm trong một mặt phẳng.
D. Hai đường thẳng cùng song song với đường thẳng thứ ba.
Gợi ý đáp án: Chọn đáp án A
Bài 2 trang 120
Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
A. 1
B. 2
C. 3
D. 4
Gợi ý đáp án: Chọn đáp án D
Bài 3 trang 120
Trong không gian, đường thẳng song song với mặt phẳng khi và chỉ khi:
A. Đường thẳng đó song song với một đường thẳng thuộc mặt phẳng.
B. Đường thẳng và mặt phẳng không có điểm chung.
C. Đường thẳng đó không có điểm chung với một đường thẳng thuộc mặt phẳng.
D. Đường thẳng đó không có điểm chung với hai đường thẳng thuộc mặt phẳng.
Gợi ý đáp án: Chọn đáp án B
Bài 4 trang 120
Trong không gian, hai mặt phẳng song song với nhau khi và chỉ khi:
A. Có một mặt phẳng chứa hai đường thẳng phân biệt cùng song song với mặt phẳng còn lại.
B. Hai mặt phẳng cùng song song với một đường thẳng.
C. Hai mặt phẳng cùng song song với mặt phẳng thứ ba.
D. Hai mặt phẳng không có điểm chung.
Gợi ý đáp án: Chọn đáp án A
Bài 5 trang 120
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, BD. Điểm P thuộc cạnh AC sao cho PA = 2PC.
a) Xác định giao điểm E của đường thẳng MP với mặt phẳng (BCD).
b) Xác định giao điểm Q của đường thẳng CD với mặt phẳng (MNP).
c) Xác định giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) Gọi I là giao điểm của MQ và NP, G là trọng tâm của tam giác ABD. Chứng minh rằng C, I, G thẳng hàng.
Gợi ý trả lời
a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d)  ACN có:
ACN có: 
Suy ra: PG // CN
Do đó:  PIG đồng dạng với
PIG đồng dạng với  NIC
NIC
Do đó: C, I, G thẳng hàng.
Bài 6 trang 120
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, SD. Xác định giao tuyến của mặt phẳng (AMN) với mỗi mặt phẳng sau:
a) (SCD);
b) (SBC).
Gợi ý trả lời
a) Ta có: AM cắt CD tại E nên E thuộc (AMN) và (SCD)
Mà N thuộc (AMN) và (SCD)
Do đó: EN là giao tuyến của hai mặt phẳng cần tìm.
b) Ta có: En cắt SC tại F nên F thuộc (AMN) và (SBC)
Mà M thuộc (AMN) và (SBC)
Do đó: FM là giao tuyến của hai mặt phẳng cần tìm.
Bài 7 trang 121
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB CD) và AB = 2CD. Gọi M, N lần lượt là trung điểm các cạnh SA, SB. Chứng minh rằng:
CD) và AB = 2CD. Gọi M, N lần lượt là trung điểm các cạnh SA, SB. Chứng minh rằng:
a) MN  (SCD);
(SCD);
b) DM  (SBC);
(SBC);
c) Lấy điểm I thuộc cạnh SD sao cho  . Chứng minh rằng: SB
. Chứng minh rằng: SB  (AIC).
(AIC).
Gợi ý trả lời
a)  SAB có: M, N là trung điểm của SA, SB nên MN // AB
SAB có: M, N là trung điểm của SA, SB nên MN // AB
Mà AB // CD
Suy ra MN // CD mà CD thuộc (SCD)
Do đó: MN // (SCD)
b) Ta có: MN =  AB
AB
Mà CD =  AB
AB
Suy ra: MN = CD mà MN // CD
Nên MNCD là hình bình hành. Do đó MD // CN
Mà CN thuộc (SBC)
Suy ra: DM // (SBC).
c) Gọi G là giao điểm của DM và AI; H là trung điểm của AB; O là giao điểm của AC và DH
Ta có: AHCD là hình bình hành vì AH // CD, AH = CD
Do đó: O là trung điểm của AC và DH
Ta chứng minh được G là trung điểm của DM
 DMH có: G, O là trung điểm của DM, DH
DMH có: G, O là trung điểm của DM, DH
Suy ra: GO // MH
Mà MH // SB (M, H là trung điểm của SA, AB)
Do đó: GO // SB mà GO thuộc (AIC) nên SB // (AIC).
Bài 8 trang 121
Cho hình lăng trụ tam giác ABC.A'B'C'. Lấy M, M' lần lượt là trung điểm các đoạn thẳng BC, B'C'; lấy các điểm G, G', K lần lượt thuộc các đoạn AM, A'M', A'B sao cho  .
.
a) Chứng minh rằng C'M  (A'BM').
(A'BM').
b) Chứng minh rằng G'K  (BCC'B').
(BCC'B').
c) Chứng minh rằng (GG'K)  (BCC'B').
(BCC'B').
d) Gọi ( ) là mặt phẳng đi qua K và song song với mặt phẳng (ABC). Mặt phẳng (
) là mặt phẳng đi qua K và song song với mặt phẳng (ABC). Mặt phẳng ( ) cắt cạnh CC' tại điểm I. Tính
) cắt cạnh CC' tại điểm I. Tính  .
.
Gợi ý trả lời
a) Ta có: MBM'C' là hình bình hành nên C'M // BM'
Mà BM' thuộc (A'BM')
Suy ra: C'M // (A'BM')
b)  A'BM' có:
A'BM' có: 
Nên G'K // BM' mà BM' thuộc (BCC'B')
Suy ra: G'K // (BCC'B')
c) Hình bình hành AMM'A' có: GG' // MM'
Mà MM' thuộc (BCC'B')
Suy ra: GG' // (BCC'B')
Mà G'K // (BCC'B')
Do đó: (GG'K) // (BCC'B')
d) Từ K kẻ đường thẳng d cắt AA' tại E, cắt BB' tại F
Do  // (ABC)
// (ABC)
Nên từ E kẻ đường thẳng // AC
Từ F kẻ đường thẳng // BC
Do đó: hai đường thẳng này cắt nhau tại I
Hình bình hành ACC'A' có: EI // AC // A'C'
Suy ra:  (1)
(1)
 A'BA có: EK // AB
A'BA có: EK // AB
Suy ra:  nên
nên  (2)
(2)
(1)(2) suy ra: 
Bài 9 trang 121
Cho hình hộp ABCD.A'B'C'D'. Gọi M, N lần lượt là trung điểm của AB, C'D'.
a) Chứng minh rằng (A'DN)  (B'CM).
(B'CM).
b) Gọi E, F lần lượt là giao điểm của đường thẳng D'B với các mặt phẳng (A'DN), (B'CM). Chứng minh rằng D'E = BF =  EF.
EF.
Gợi ý trả lời
a) Hình bình hành CDA'B' có: A'D // B'C
Mà B'C thuộc (B'CM)
Suy ra: A'D // (B'CM) (1)
Gọi P là trung điểm của A'B'
Dễ dàng chứng minh được AMB'P là hình bình hành
Do đó: B'M // AP
Ta có: PN // A'D' mà A'D' // AD nên PN // AD
PN = A'D' mà A'D' = AD nên PN = AD
Do đó: PADN là hình bình hành
Suy ra: AP // DN
Do đó: B'M // DN mà B'M thuộc (B'CM)
Suy ra: DN // (B'CM) (2)
(1)(2) suy ra (A'DN) // (B'CM)
b) Ta có: A'N cắt D'B' tại K
Có: DK cắt D'B
Mà DK thuộc (A'DN)
D'B cắt (A'DN) tại E
Do đó: DK cắt D'B tại E
Ta có:  A'KB' đồng dạng với
A'KB' đồng dạng với  NKD' (do A'B' // D'N)
NKD' (do A'B' // D'N)
Suy ra: 
Do đó:  mà D'B' = DB
mà D'B' = DB
Nên: 
Có:  EDB đồng dạng với
EDB đồng dạng với  EKD' (do DB // D'K)
EKD' (do DB // D'K)
Suy ra: 
Nên:  hay
hay 
Chứng minh tương tự ta được: 
Do đó: D'E = BF =  EF.
EF.
Bài 10 trang 121
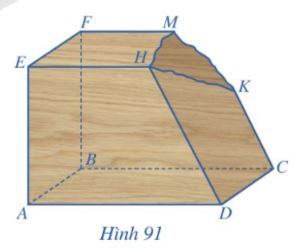
Một khối gỗ có các mặt đều là một phần của mặt phẳng với (ABCD)  (EFMH), CK
(EFMH), CK  DH. Khối gỗ bị hỏng một góc (Hình 91). Bác thợ mộc muốn làm đẹp khối gỗ bằng cách cắt khối gỗ theo mặt phẳng (R) đi qua K và song song với mặt phẳng (ABCD).
DH. Khối gỗ bị hỏng một góc (Hình 91). Bác thợ mộc muốn làm đẹp khối gỗ bằng cách cắt khối gỗ theo mặt phẳng (R) đi qua K và song song với mặt phẳng (ABCD).
a) Hãy giúp bác thợ mộc xác định giao tuyến của mặt phẳng (R) với các mặt của khối gỗ để cắt được chính xác.
b) Gọi I, J lần lượt là giao điểm DH, BF với mặt phẳng (R). Biết BF = 60 cm, DH = 75 cm, CK = 40 cm. Tính FJ.
Gợi ý trả lời
a)
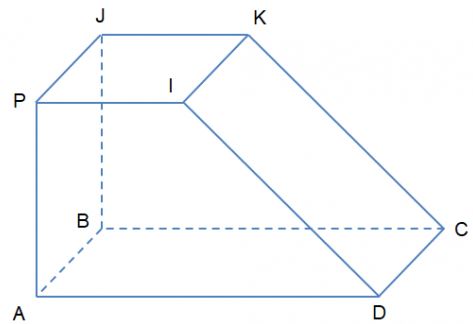
Từ K kẻ KJ //BC // MH
Từ K kẻ KI // CD
Từ J kẻ JP // AB
Từ P kẻ PI // AD
Từ đó ta được (KJPI) trùng với (R) đi qua K và song song với (ABCD)
b) Ta có: DI = KC = 40
Suy ra: IH = DH - ID = 75 - 40 = 35
Do đó: 
Mà EH // IP // AD
Suy ra: 
Mà EF // PJ // AB
Suy ra: 
Mà BF = 60
Nên  . Do đó: FJ = 28 (cm).
. Do đó: FJ = 28 (cm).
