Giải Toán lớp 9 trang 99, 100, 101 tập 1 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và bài tập trong SGK bài 1 Sự xác định đường tròn, tính chất đối xứng của đường tròn thuộc chương 2.
Giải Toán 9 Bài 1 Chương 2 tập 1 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 99, 100, 101 tập 1 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Toán 9 Bài 1: Sự xác định đường tròn, tính chất đối xứng của đường tròn
- Trả lời câu hỏi Toán 9 Bài 1 chương 2
- Giải bài tập Toán 9 trang 99, 100, 101 tập 1
- Giải Toán 9 trang 100, 101 tập 1: Luyện tập
Trả lời câu hỏi Toán 9 Bài 1 chương 2
Câu hỏi 1
Trên hình 53, điểm H nằm bên ngoài đường tròn (O), điểm K nằm bên trong đường tròn (O). Hãy so sánh ![]()
Gợi ý đáp án
Ta có: OH > R > OK
![]()
(Góc đối diện với cạnh lớn hơn thì lớn hơn)
Câu hỏi 2
Cho hai điểm A, B
a) Hãy vẽ một đường tròn đi qua hai điểm đó.
b) Có bao nhiêu đường tròn như vậy? Tâm của chúng nằm trên đường nào?
Gợi ý đáp án
A. Học sinh tự vẽ
b) Có vô số đường tròn đi qua hai điểm. Tâm của chúng nằm trên đường trung trực của đoạn thẳng đó
Câu hỏi 3
Cho ba điểm A, B, C không thẳng hàng. Hãy vẽ đường tròn đi qua ba điểm đó.
Gợi ý đáp án
Do ba điểm A, B, C không thẳng hàng
=> A, B, C tạo thành một tam giác
Do đường tròn cần tìm đi qua ba điểm
=> Đường tròn đó là đường tròn ngoại tiếp tam giác ABC.
Cách vẽ đường tròn như sau:
Bước 1: Nối AB và AC
Bước 2: Vẽ các đường trung trực của AB và AC. Giao điểm hai đường trung trực đó là tâm đường tròn ngoại tiếp ba điểm A, B, C
Hình vẽ minh họa
Câu hỏi 4
Cho đường tròn (O), A là một điểm bất kì thuộc đường tròn. Vẽ A’ đối xứng với A qua điểm O (h. 56). Chứng minh rằng điểm A; cũng thuộc đường tròn (O).
Gợi ý đáp án
Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)
Giải bài tập Toán 9 trang 99, 100, 101 tập 1
Bài 1
Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Gợi ý đáp án
Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có OA = OB = OC = OD (tính chất) nên bốn điểm A, B, C, D thuộc cùng một đường tròn (tâm O, bán kính OA)
Theo định lí Pitago trong tam giác vuông ABC có:
![]()
![]()
![]()
Nên bán kính đường tròn là OA = 6.5 cm
Bài 2
Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng:
| (1) Nếu tam giác có ba góc nhọn | (4) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên ngoài tam giác |
| (2) Nếu tam giác có góc vuông | (5) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên trong tam giác |
| (3) Nếu tam giác có góc tù | (6) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh lớn nhất |
| (7) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh nhỏ nhất |
Gợi ý đáp án
- Nối (1) - (5)
- Nối (2) - (6)
- Nối (3) - (4)
Bài 3
Chứng minh các định lí sau:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Gợi ý đáp án
Vẽ hình minh họa
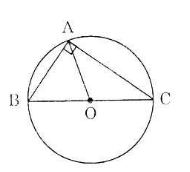
Hình a) + b)
a) Xét tam giác ABC vuông tại A. Gọi O là trung điểm của BC.
Ta có AO là đường trung tuyến ứng với cạnh huyền nên OA = OB = OC.
=> O là tâm của đường tròn đi qua A, B, C.
Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:
OA = OB = OC
Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên suy ra tam giác ABC vuông tại A. (đpcm)
Bài 4
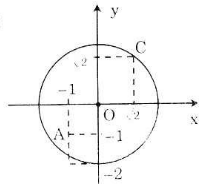
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(-1; -1), B(-1; -2), C(√2; √2) đối với đường tròn tâm O bán kính 2.
Gợi ý đáp án
Gọi R là bán kính của đường tròn O: R = 2
Ta có:
OA2 = 12 + 12 = 2 => OA = √2 < R
=> A nằm bên trong (O)
OB2 = 12 + 22 = 5 => OB = √5 > R
=> B nằm bên ngoài (O)
OC2 = (√2)2 + (√2)2 = 4 => OC = 2 = R
=> C nằm trên (O)
Bài 5
Đố. Một tấm bài hình tròn không còn dấu vết của tâm. Hãy tìm lại tâm của hình tròn đó
Gợi ý đáp án
- Cách 1:
- Lấy 3 điểm bất kì trên hình tròn. Vẽ hai dây AB và AC.
- Vẽ đường trung trực của AB và AC. Giao điểm O của đường trung trực này chính là tâm của hình tròn.

- Cách 2:
- Gấp tấm bìa sao cho hai phần của hình tròn trùng nhau, nếp gấp là một đường kính.
- Lại gấp như trên theo nếp gấp khác, ta được một đường kính thứ hai. Giao điểm của hai đường kính này là tâm của đường tròn

Giải Toán 9 trang 100, 101 tập 1: Luyện tập
Bài 6
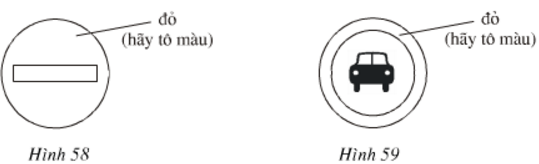
Trong các biển báo giao thông sau, biển báo nào có tâm đối xứng, biển nào có trục đối xứng?
a) Biển cấm đi ngược chiều? (h.58)
b) Biển cấm ô tô (h.59)
Gợi ý đáp án
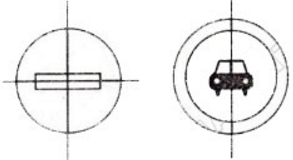
- Hình 58 có tâm đối xứng là tâm đường tròn, có hai trục đối xứng là hai đường kính vuông góc với các cạnh của hình chữ nhật trong đường tròn.
- Hình 59 có một trục đối xứng, không có tâm đối xứng.
Bài 7
Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng:
| (1) Tập hợp các điểm có khoảng cách đến điểm A cố định bằng 2cm | (4) là đường tròn tâm A bán kính 2cm |
| (2) Đường tròn tâm A bán kính 2cm gồm tất cả những điểm | (5) có khoảng cách đến điểm A nhỏ hơn hoặc bằng 2cm |
| (3) Hình tròn tâm A bán kính 2cm gồm tất cả những điểm | (6) có khoảng cách đến điểm A bằng 2cm |
| (7) có khoảng cách đến điểm A lớn hơn 2cm |
Gợi ý đáp án
- Nối (1) - (4)
- Nối (2) - (6)
- Nối (3) - (5)
Bài 8
Cho góc nhọn xAy và hai điểm B, C thuộc tia Ax. Dựng đường tròn (O) đi qua B và C sao cho tâm O nằm trên tia Ay.
Gợi ý đáp án

- Tâm O là giao điểm giữa đường trung trực của BC và tia Ay. Nên ta có cách dựng:
+ Dựng đường trung trực (d) của BC. (d) cắt tia Ay tại O.
+ Vẽ đường tròn (O, OB). Đường tròn này đi qua B, C. Đó là đường tròn cần dựng.
- Chứng minh:
+ Vì O ∈ đường trung trực (d) của BC nên OB = OC. Suy ra (O, OB) đi qua B, C
+ Vì O ∈ Ay nên (O, OB) thỏa mãn điều kiện đề bài.
Bài 9
Đố
a) Vẽ hình hoa bốn cánh. Hình hoa bốn cánh trên hình 60 được tạo bởi một hình vuông và tâm của cung là tâm của đường tròn chứa cung đó). Hãy vẽ lại hình 60 vào vở.
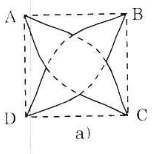
Hình 60
b) Vẽ lọ hoa. Chiếc lọ hoa trên hình 61 được vẽ trên giấy kẻ ô vuông bởi năm cung có tâm A, B, C, D, E. Hãy vẽ lại hình 61 vào giấy kẻ ô vuông.
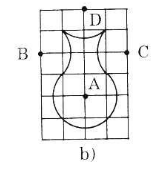
Hình 61
Gợi ý đáp án
a) Cách vẽ:
- Vẽ hình vuông ABCD.
- Vẽ cung tròn tâm A, bán kính là cạnh hình vuông. Cung tròn này đi qua B, D.
- Tương tự với các cung tròn còn lại.
Ta được bốn cung tròn tạo thành hình hoa bốn cánh.
b) Cách vẽ:
- Kẻ lại các ô vuông và lấy các điểm như hình 61.
- Lần lượt vẽ các cung tròn có tâm là các điểm A, B, C, D, E và bán kính là đường chéo của ô vuông.
Ta được năm cung tròn liền nét với nhau tạo thành hình chiếc lọ hoa.
Lý thuyết Toán 9 bài 1
1. Định nghĩa đường tròn
Đường tròn tâm O bán kính R, kí hiệu (O;R), là hình gồm các điểm cách O một khoảng bằng R.
- Nếu A nằm trên đường tròn (O;R) thì OA=R
- Nếu A nằm trong đường tròn (O; R) thì OA<R
- Nếu A nằm ngoài đường tròn (O;R) thì OA>R.
2. Định lí về sự xác định một đường tròn
Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
Tâm O của đường tròn đi qua ba điểm A, B, C là giao điểm của ba đường trung trực của tam giác ABC.
3. Tính chất đối xứng của đường tròn
a) Tâm đối xứng
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
b) Trục đối xứng
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
