Giải bài tập Toán 9 Bài 6: Cung chứa góc để xem gợi ý giải các bài tập trang 86, 87 thuộc chương trình Hình học lớp 9 tập 2.
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa trang 86, 87 Toán lớp 9 tập 2. Qua đó giúp học sinh lớp 9 tham khảo nắm vững hơn kiến thức trên lớp. Mời các bạn cùng theo dõi bài tại đây.
Giải Toán 9 Bài 6: Cung chứa góc
Lý thuyết Cung chứa góc
Quỹ tích cung chứa góc
Với đoạn thẳng AB và góc α (0 < α < 180°) cho trước thì quỹ tích các điểm M thoả mãn ∠AMB = a là hai cung chứa góc α dựng trên đoạn AB.
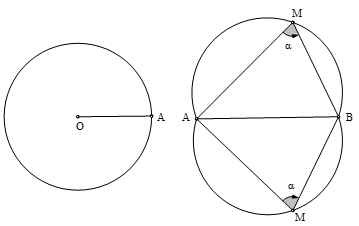
Chú ý:
+ Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB.
+ Hai điểm A, B được coi là thuộc quỹ tích.
+ Đặc biệt: Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.
Cách vẽ cung chứa góc α
– Vẽ đường trung trực d của đoạn thẳng AB.
– Vẽ tia Ax tạo với AB một góc α.
– Vẽ đường thẳng Ay vuông góc với Ax. Gọi O là giao điểm của Ay với d.
– Vẽ cung AmB, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax.
-Góc AmB được vẽ như trên là một cung chứa góc α.
Cách giải bài toán quỹ tích
Muốn chứng minh quỹ tích (tập hợp) các điểm M thoả mãn tính chất T là một hình H nào đó, ta phải chứng minh hai phần:
– Phần thuận: Mọi điểm có tính chất T đều thuộc hình H.
– Phần đảo: Mọi điểm thuộc hình H đều có tính chất T.
– Kết luận: Quỹ tích các điểm M có tính chất T là hình H.
Giải bài tập toán 9 trang 86, 87 Tập 2
Bài 44 (trang 86 SGK Toán 9 Tập 2)
Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.
Vẽ hình minh họa:
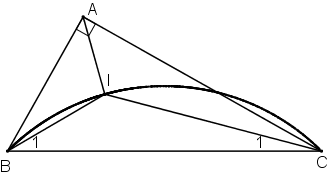
*Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.
* Chứng minh :
Phần thuận :
Điểm A luôn nhìn đoạn thẳng AB dưới một góc 90^\circ nên quỹ tích điểm A là đường tròn đường kính BC.
Xét tam giác ABC vuông tại A nên ![]() lại có BI là phân giác góc B và CI là phân giác góc C nên
lại có BI là phân giác góc B và CI là phân giác góc C nên
![]()
Xét tam giác IBC có ![]()
Nên số đo góc BIC luôn không đổi.
Vậy khi điểm A thay đổi trên đường tròn đường kính BC thì điểm I thay đổi và luôn nhìn đoạn thẳng BC dưới một góc ![]()
Vậy điểm I thuộc hai cung chứa góc ![]() dựng trên đoạn BC.
dựng trên đoạn BC.
Phần đảo:
Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của góc CBx
+ Kẻ tia Cy sao cho CI là phân giác của góc BCy
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
Ta có:

Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận: Quĩ tích các điểm I là hai cung chứa góc ![]() dựng trên đoạn BC.
dựng trên đoạn BC.
Bài 45 (trang 86 SGK Toán 9 Tập 2)
Cho các hình thoi ABCD có cạnh AB cố định. TÌm quỹ tích giao điểm O của hai đường chéo của các hình thoi đó.
Vẽ hình
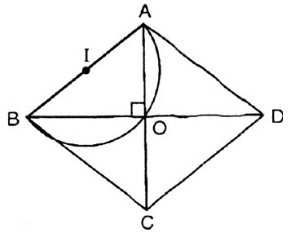
Dự đoán: Quỹ tích cần tìm là nửa đường tròn đường kính AB.
Chứng minh:
Phần thuận:
Ta đã biết rằng hai đường chéo hình thoi vuông góc với nhau hay ![]() tại O.
tại O.
Vậy điểm O nhìn AB cố định dưới góc ![]()
![]() Quỹ tích điểm O là nửa đường tròn đường kính AB.
Quỹ tích điểm O là nửa đường tròn đường kính AB.
Phần đảo:
Chứng minh với mọi điểm O thuộc nửa đường tròn đường kính AB ta đều có hình thoi ABCD thỏa mãn đề bài.
+ Lấy điểm O thuộc nửa đường tròn đường kính AB
+ Lấy C đối xứng với A qua O
+ Lấy D đối xứng với B qua O.
Tứ giác ABCD có AC cắt BD tại O là trung điểm mỗi đường
⇒ ABCD là hình bình hành.
Mà O thuộc nửa đường tròn đường kính AB
![]()
⇒ AC ⊥ DB
⇒ Hình bình hành ABCD là hình thoi.
Kết luận: Quỹ tích điểm O là nửa đường tròn đường kính AB (khác A và B)
Bài 46 (trang 86 SGK Toán 9 Tập 2)
Dựng một cung chứa góc 55o trên đoạn thẳng AB = 3cm.
Vẽ hình:
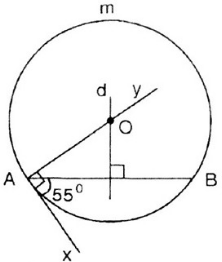
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm).
- Dựng góc ![]() (dùng thước đo góc và thước thẳng).
(dùng thước đo góc và thước thẳng).
- Dựng tia Ay vuông góc với Ax (dùng êke).
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chia khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa).
Ta có: ![]() là cung chứa góc
là cung chứa góc ![]() dựng trên đoạn thẳng AB = 3cm (một cung).
dựng trên đoạn thẳng AB = 3cm (một cung).
Chứng minh:
+ O thuộc đường trung trực của AB
⇒ OA = OB
⇒ B thuộc đường tròn (O; OA).
Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).
⇒ Góc BAx là góc tạo bởi tiếp tuyến Ax và dây AB
Lấy M ∈ cung AmB thì góc AMB là góc nội tiếp chắn cung nhỏ AB
![]()
⇒ Cung AmB là cung chứa góc 55º dựng trên đoạn AB = 3cm.
Kết luận: Bài toán có một nghiệm hình.
Bài 47 (trang 86 SGK Toán 9 Tập 2)
Gọi cung chứa góc 55o ở bài tập 46 là cung AmB. Lấy điểm M1 nằm bên trong và điểm M2 nằm bên ngoài đường tròn chứa cung này sao cho M1, M2 và cung AmB nằm cùng một phía đối với đường thẳng AB. Chứng minh rằng:
a) ![]()
b) ![]()
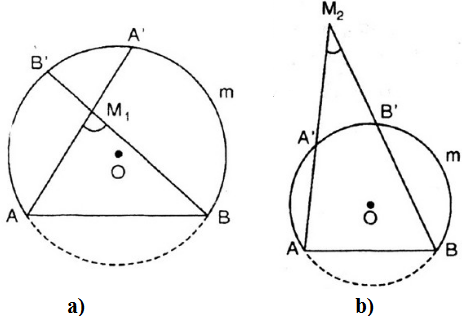
Gọi A', B’ theo thứ tự là giao điểm của ![]() với cung tròn.
với cung tròn.
Ta có ![]() (góc nội tiếp chắn cung AB và cung AmB là cung chứa góc
(góc nội tiếp chắn cung AB và cung AmB là cung chứa góc ![]() )
)
Vì ![]() là góc có đỉnh nằm trong đường tròn chắn cung A'B' và AB nên:
là góc có đỉnh nằm trong đường tròn chắn cung A'B' và AB nên:

Vậy ![]()
b) ![]() là điểm bất kì nằm ngoài đường tròn (hình vẽ )
là điểm bất kì nằm ngoài đường tròn (hình vẽ )
Ta có ![]() lần lượt cắt đường tròn tại A’, B’.
lần lượt cắt đường tròn tại A’, B’.
![]() (góc nội tiếp chắn cung AB và cung AmB là cung chứa góc
(góc nội tiếp chắn cung AB và cung AmB là cung chứa góc ![]() )
)
Vì góc ![]() là góc có đỉnh nằm bên ngoài đường tròn chắn cung A'B' và AB nên:
là góc có đỉnh nằm bên ngoài đường tròn chắn cung A'B' và AB nên:

Vậy ![]()
Giải bài tập toán 9 trang 87 Tập 2: Luyện tập
Bài 48 (trang 87 SGK Toán 9 Tập 2)
Cho hai điểm A, B cố định. Từ A vẽ các tiếp tuyến với các đường tròn tâm B có bán kính không lớn hơn AB. Tìm quỹ tích các tiếp điểm.
Vẽ hình minh họa
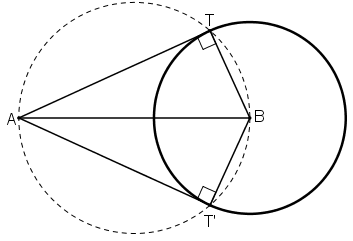
Dự đoán: Quỹ tích là đường tròn đường kính AB.
+ Phần thuận:
Tiếp tuyến TA vuông góc với bán kính BT tại tiếp điểm T.
Suy ra ![]()
Do AB cố định nên quỹ tích của T là đường tròn đường kính AB.
+ Phần đảo:
Lấy T thuộc đường tròn đường kính AB
![]()
⇒ AT ⊥ TB và BT < AB
⇒ AT tiếp xúc với đường tròn tâm B, bán kính BT < BA.
Kết luận: Quỹ tích các tiếp điểm là đường tròn đường kính AB.
Bài 49 (trang 87 SGK Toán 9 Tập 2)
Dựng tam giác ABC, biết BC = 6cm, góc A = 40o và đường cao AH = 4cm.
Vẽ hình minh họa
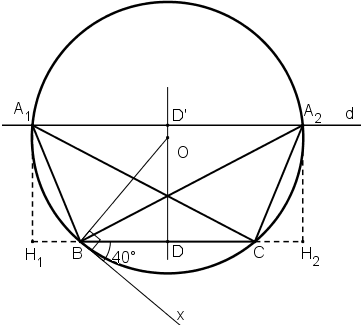
Cách dựng:
+ Kẻ đoạn thẳng AB = 6cm
+ Dựng cung chứa góc ![]() trên đoạn BC.
trên đoạn BC.
- Vẽ đường trung trực d của đoạn BC
- Vẽ tia Bx tạo với BC góc ![]()
- Vẽ tia ![]() , tia By cắt đường thẳng d tại O. Vẽ cung BmC tâm O bán kính OB sao cho cung này nằm ở nửa mặt phẳng bờ BC không chứa Bx. Cung BmC chính là cung chứa góc 40^\circ cần dựng.
, tia By cắt đường thẳng d tại O. Vẽ cung BmC tâm O bán kính OB sao cho cung này nằm ở nửa mặt phẳng bờ BC không chứa Bx. Cung BmC chính là cung chứa góc 40^\circ cần dựng.
+ Vẽ đường thẳng t song song với BC và cách BC một khoảng 4cm. Gọi giao điểm của đường thẳng t với cung BmC là A và A'.
Khi đó có hai tam giác thỏa mãn đề bài là ABC hoặc tam giác A'BC.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC
![]()
+ A ∈ t song song với BC và cách BC 4cm nên chiều cao của tam giác ABC là 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Bài 50 (trang 87 SGK Toán 9 Tập 2)
Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB.
a) Chứng minh ![]() không đổi.
không đổi.
b) Tìm tập hợp các điểm I nói trên.
Vẽ hình minh họa:
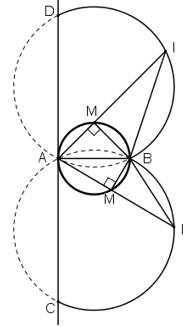
a) Gọi O là trung điểm AB. Xét đường tròn tâm O có ![]() là góc nội tiếp chắn nửa đường tròn nên
là góc nội tiếp chắn nửa đường tròn nên ![]() hay
hay ![]()
Xét tam giác vuông MBI có ![]()
Suy ra ![]() không đổi và thỏa mãn
không đổi và thỏa mãn ![]()
b) Phần thuận:
Khi điểm M thay đổi trên đường tròn đường kính AB thì điểm I thay đổi và luôn nhìn cạnh AB dưới một góc ![]() không đổi (với
không đổi (với ![]() )
)
Vậy điểm I thuộc hai cung chứa góc ![]() sao cho
sao cho ![]() dựng trên đoạn AB.
dựng trên đoạn AB.
Nhưng tiếp tuyến PQ với đường tròn đường kính AB tại A là vị trí giới hạn của AM. Do đó điểm I thuộc hai cung PmB,Qm'B.
Hai điểm P, Q là các điểm giới hạn của quỹ tích, điểm B là điểm đặc biệt của quỹ tích
Phần đảo:
Lấy điểm I' bất kỳ thuộc cung Qm'B (hoặc cung PmB). Nối AI' cắt đường tròn tâm O tại M'. Ta chứng minh M'I' = 2M'B.
Xét ![]() có
có ![]() là góc nội tiếp chắn nửa đường tròn nên
là góc nội tiếp chắn nửa đường tròn nên ![]()
Xét tam giác BM'I' vuông ở M' có ![]() (do I' bất kỳ thuộc cung Qm'B là cung chứa góc
(do I' bất kỳ thuộc cung Qm'B là cung chứa góc ![]() dựng trên đoạn AB) nên
dựng trên đoạn AB) nên ![]() mà
mà ![]()
Kết luận: Quỹ tích các điểm I là hai cung PmB,Qm'B.
Bài 51 (trang 87 SGK Toán 9 Tập 2)
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = 60o. Gọi H là giao điểm của các đường cao BB'và CC'.
Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
Vẽ hình
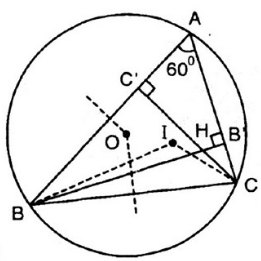
+) Ta có: ![]() (góc nội tiếp và góc ở tâm cùng chắn một cung BC). (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung BC). (1)
+) Lại có ![]() (hai góc đối đỉnh)
(hai góc đối đỉnh)
Mà ![]()
![]() (2)
(2)
+) Vì I là tâm đường tròn nội tiếp tam giác ABC nên BI; CI lần lượt là tia phân giác góc B, góc C.
Xét tam giác ABC có ![]()
Xét tam giác BIC theo định lý về tổng 3 góc trong một tam giác ta có

Do đó ![]() (3)
(3)
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc ![]() dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O,\, H, I cùng thuộc một đường tròn.
dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O,\, H, I cùng thuộc một đường tròn.
Bài 52 (trang 87 SGK Toán 9 Tập 2)
"Góc sút" của quả phạt đền 11 mét là bao nhiêu độ? Biết rằng chiều rộng cầu môn là 7,32m. Hãy chỉ ra hai vị trí khác trên sân có cùng "góc sút" như quả phạt đền 11 mét.
Vẽ hình
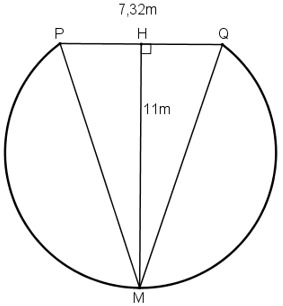
Gọi vị trí đặt bóng để sút phạt đền là M, và bề ngang cầu môn là PQ thì M nằm trên đường trung trực của PQ.
Gọi H là trung điểm PQ, ![]()
Do M nằm trên đường trung trực của PQ nên MH vuông góc PQ.
Tam giác MPH vuông tại H, áp dụng tỉ số lượng giác trong tam giác vuông ta có:
![]()
Vậy góc sút phạt đền là ![]()
Vẽ cung chứa góc ![]() dựng trên đoạn thẳng PQ. Bất cứ điểm nào trên cung vừa vẽ cũng có “góc sút” như quả phạt đền 11m.
dựng trên đoạn thẳng PQ. Bất cứ điểm nào trên cung vừa vẽ cũng có “góc sút” như quả phạt đền 11m.
