Giải Toán 9 trang 68, 69, 70 Tập 2 giúp các bạn học sinh tham khảo cách giải, đối chiếu với lời giải hay chính xác phù hợp với năng lực của các bạn lớp 9.
Giải Toán lớp 9 Bài 1: Góc ở tâm, Số đo cung thuộc chương trình Hình học 9 Chương 3 được biên soạn đầy đủ tóm tắt lý thuyết, trả lời các câu hỏi phần bài tập cuối bài trang 68, 69, 70. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm, củng cố, bồi dưỡng và kiểm tra vốn kiến thức của bản thân. Vậy sau đây là nội dung chi tiết giải bài tập Toán 9 bài 1 chương 3 Hình học, mời các bạn cùng theo dõi tại đây.
Giải Toán 9 Bài 1: Góc ở tâm. Số đo cung
Lý thuyết Góc ở tâm. Số đo cung
1. Góc ở tâm
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm
2. Số đo cung
Số đo cung của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Số đo của cung lớn bằng 360^0 trừ đi số đo của cung nhỏ
Số đo của nửa đường tròn bằng 180^0
Chú ý:
- Cung nhỏ có số đo nhỏ hơn 180^0
- Cung lớn có số đo lớn hơn 180^0
- Cung có điểm đầu, điểm cuối trùng nhau có số đo 0^0.
- Cung có cả đường tròn có số đo là 360^0
3. So sánh hai cung
Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau
Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.
- Khi nào thì sđ ![]() = sđ
= sđ ![]() + sđ
+ sđ ![]() ?
?
Nếu C là một điểm nằm trên cung AB thì:
sđ ![]() = sđ
= sđ ![]() + sđ
+ sđ ![]()
4. Các dạng toán thường gặp
Tính số đo của góc ở tâm, tính số đo của cung bị chắn. So sánh các cung.
Phương pháp:
Ta sử dụng các kiến thức sau:
- Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó
- Số đo của cung lớn bằng hiệu giữa 360o
và số đo của cung nhỏ (có chung hai đầu mút với cung lớn).
- Số đo của nửa đường tròn bằng 180o Cung cả đường tròn có số đo 360o
- Sử dụng tỉ số lượng giác của một góc nhọn để tính góc.
- Sử dụng quan hệ đường kính và dây cung.
Trả lời câu hỏi Toán 9 Bài 1
Câu hỏi 1
Vẽ một đường tròn rồi vẽ hai cung có số đo bằng nhau
Vẽ một đường tròn tâm O bất kì.
Vẽ hai đường kính CD, EF bất kì của đường tròn tâm O.
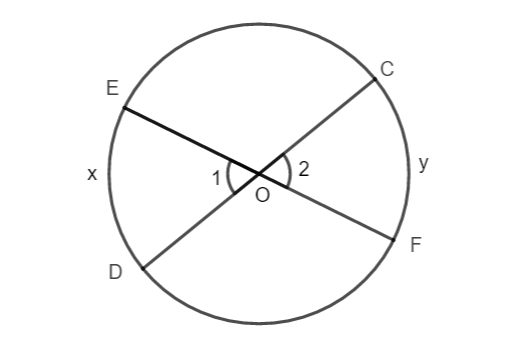
Ta có: ![]() (đối đỉnh)
(đối đỉnh)
Do số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó
![]()
Câu hỏi 2
Hãy chứng minh đẳng thức ![]() trong trường hợp điểm C nằm trên cung nhỏ AB (h.3)
trong trường hợp điểm C nằm trên cung nhỏ AB (h.3)
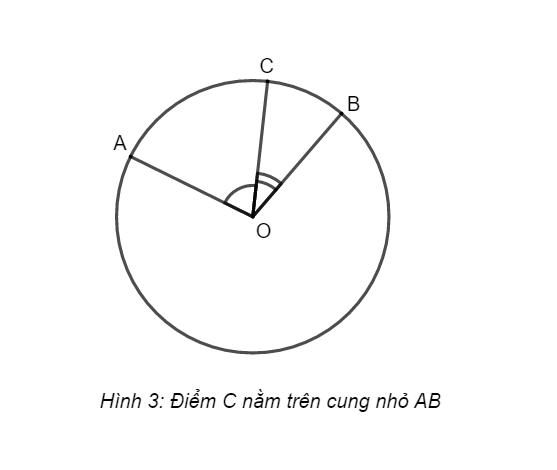
Do điểm C nằm giữa hai điểm A và B ![]()
Mà số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó

Giải Toán 9 trang 68, 69, 70 tập 2
Bài 1
Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu độ vào những thời điểm sau:
a) 3 giờ;
b) 5 giờ;
c) 6 giờ;
d) 12 giờ;
e) 20 giờ?

Trên mặt đồng hồ người ta chia thành 12 phần bằng nhau. Góc ở tâm tạo bởi hai kim giữa hai số liền nhau là:
360o : 12 = 30o
a) Thời điểm 3 giờ (hình a) thì góc ở tâm có số đo là: 3.30o = 90o
b) Thời điểm 5 giờ (hình b) thì góc ở tâm có số đo là: 5. 30o = 150o
c) Thời điểm 6 giờ (hình c) thì góc ở tâm có số đo là: 6.30o = 180o
d) Thời điểm 12 giờ (hình d) thì góc ở tâm có số đo là: 0o
e) Thời điểm 20 giờ (hình e) thì góc ở tâm có số đo là: 4.30o= 120o
Bài 2
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40o. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Vẽ hình
 Ta có
Ta có ![]() , suy ra
, suy ra ![]() (hai góc đối đỉnh)
(hai góc đối đỉnh)
Lại có ![]() (hai góc kề bù) nên
(hai góc kề bù) nên ![]()
Lại có ![]() (hai góc đối đỉnh)
(hai góc đối đỉnh)
Vậy ![]()
và ![]()
Bài 3
Trên các hình 5, 6 hãy dùng dụng cụ đo góc để tìm số đo cung AmB.
Từ đó, tính số đo cung AnB tương ứng.


Với hình 5: Ta có: ![]()
![]()
và sđ ![]()
Với hình 6
Ta có góc ![]()
=> sđ ![]()
sđ ![]()
Bài 4
Xem hình 7. Tính số đo của góc ở tâm AOB và số đo cung lớn AB.

Ta có OA = AT (gt) và góc OAT bằng 90^0 nên ∆AOT là tam giác vuông cân tại A, vậy ![]()
Suy ra số đo cung nhỏ ![]() . Do đó số đo cung lớn
. Do đó số đo cung lớn ![]() là:
là: ![]()
Bài 5
Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết góc AMB = 35o.
a) Tính số đo của góc ở tâm tạo bởi bán kính OA, OB.
b) Tính số đo mỗi cung AB (cung lớn và cung nhỏ).

a) Vì MA,MB là hai tiếp tuyến của ![]() cắt nhau tại M nên
cắt nhau tại M nên ![]()
Xét tứ giác OBMA có ![]() (định lý)
(định lý)
Hay ![]()
![]()
b) Từ ![]() . Suy ra số đo cung nhỏ
. Suy ra số đo cung nhỏ ![]() là
là ![]() và số đo cung lớn
và số đo cung lớn ![]() là:
là: ![]()
Bài 6
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
b) Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
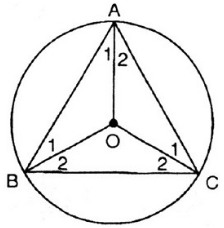 a) Ta có:
a) Ta có: ![]() (gt)
(gt)
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC.
Nên ![]()
Suy ra: ![]()
Tương tự ta suy ra: ![]()
b) Từ ![]() ta suy ra:
ta suy ra:
sđ ![]()
![]()
Bài 7
Cho hai đường tròn cùng tâm O với bán kính khác nhau. Hai đường thẳng đi qua O cắt hai đường tròn đó tại các điểm A, B, C, D, M, N, P, Q (h.8).
a) Em có nhận xét gì về số đo của các cung nhỏ AM, CP, BN, DQ?
b) Hãy nêu tên các cung nhỏ bằng nhau.
c) Hãy nêu tên hai cung lớn bằng nhau.
Vẽ hình:
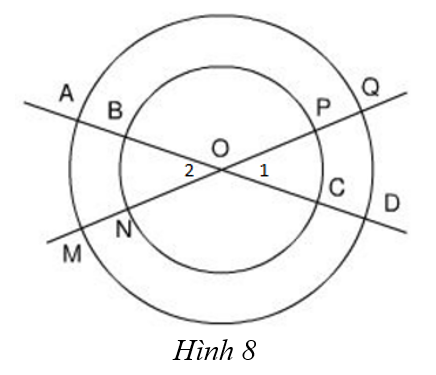 a) Các cung nhỏ
a) Các cung nhỏ ![]() có cùng số đo (cùng bằng góc BON)
có cùng số đo (cùng bằng góc BON)
b) ![]()
c) Các cung lớn bằng nhau:
![]()
Bài 8
Mỗi khẳng định sau đây đúng hay sai? Vì sao?
a) Hai cung bằng nhau thì số đo bằng nhau.
b) Hai cung có số đo bằng nhau thì bằng nhau.
c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn.
d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.
a) Đúng. Dựa vào cách so sánh hai cung (SGK trang 68).
Chú ý: Khi ta nói hai cung bằng nhau, nghĩa là hai cung này so sánh được (tức chúng cùng nằm trong một đường tròn hoặc trong hai đường tròn bằng nhau). Do đó, theo cách so sánh hai cung đã biết thì hai cung bằng nhau thì số đo bằng nhau.
b) Sai. Nếu hai cung này nằm trong hai đường tròn có bán kính khác nhau thì ta không thể so sánh hai cung.
c) Sai. (Lí luận như câu b)
d) Đúng. (Lí luận như câu a)
Bài 9
Trên đường tròn tâm O lấy ba điểm A, B, C sao cho ![]() , sđ cung
, sđ cung ![]() . Tính số đo của cung nhỏ
. Tính số đo của cung nhỏ ![]() và cung lớn
và cung lớn ![]() . (Xét cả hai trường hợp: điểm C nằm trên cung nhỏ
. (Xét cả hai trường hợp: điểm C nằm trên cung nhỏ ![]() , điểm C nằm trên cung lớn
, điểm C nằm trên cung lớn ![]()
Vẽ hình minh họa
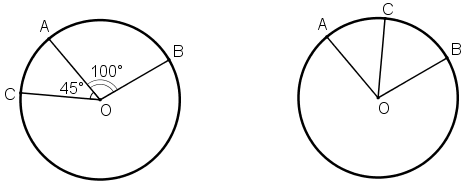
TH1: Điểm C nằm trên cung nhỏ ![]()
Số đo cung nhỏ BC là sđ ![]() = sđ
= sđ ![]()
Số đo cung lớn ![]()
TH2: Điểm C nằm trên cung lớn ![]()
Số đo cung nhỏ BC là sđ ![]() = sđ
= sđ ![]() + sđ
+ sđ ![]()
Số đo cung lớn ![]()
