Giải Toán lớp 9 trang 68, 69, 70 tập 1 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và 9 bài tập trong SGK bài 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông thuộc Chương 1: Hệ thức lượng trong tam giác vuông.
Giải Toán 9 Bài 1 tập 1 Một số hệ thức về cạnh và đường cao trong tam giác vuông được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 68, 69, 70 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Toán 9: Một số hệ thức về cạnh và đường cao trong tam giác vuông
I. Trả lời câu hỏi trang 66, 67 SGK Toán 9 tập 1
Câu hỏi 1
Xét hình 1. Chứng minh ![]() . Từ đó suy ra hệ thức (2)
. Từ đó suy ra hệ thức (2)
Lời giải chi tiết
Ta có: ![]()
Mà ![]()
Xét tam giác AHB và tam giác CHA có:
![]()

Vậy trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên hai cạnh huyền.
Câu hỏi 2
Xét hình 1. Hãy chứng minh hệ thức (3) bằng tam giác đồng dạng.
Lời giải chi tiết
Xét tam giác ABD và tam giác CAB có:
![]() chung
chung

Vậy ta có trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
II. Giải bài tập toán 9 trang 68, 69, 70 tập 1
Bài 1 (trang 68 SGK Toán 9 Tập 1)
Hãy tính x và y trong mỗi hình sau: (h.4a, b)
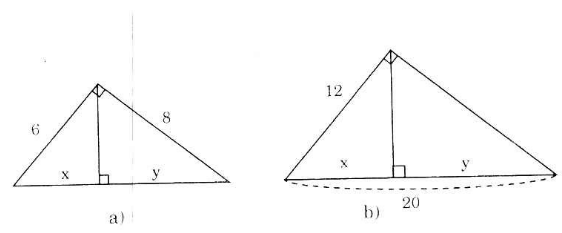
Gợi ý đáp án
a) Đặt tên các đỉnh của tam giác như hình dưới:
Áp dụng định lí Pytago vào ![]() vuông tại A, ta có:
vuông tại A, ta có:
![]()
Áp dụng hệ thức lượng vào ![]() vuông tại A, đường cao AH, ta có:
vuông tại A, đường cao AH, ta có:
![]()
Lại có HC=BC-BH=10-3,6=6,4
Vậy x =BH= 3,6; y=HC = 6,4.
b) Đặt tên các đỉnh của tam giác như hình dưới
Áp dụng hệ thức lượng vào ![]() vuông tại A, đường cao AH, ta có:
vuông tại A, đường cao AH, ta có:
![]()
Lại có: HC=BC-BH=20-7,2=12,8
Vậy x=BH = 7,2; y=HC = 12,8.
Bài 2 (trang 68 SGK Toán 9 Tập 1)
Hãy tính x và y trong mỗi hình sau: (h.5)

Gợi ý đáp án
Ta có: BC=BH + HC=1+4=5.
Xét ![]() vuông tại A, đường cao AH, áp dụng hệ thức lượng trong tam giác vuông, ta có:
vuông tại A, đường cao AH, áp dụng hệ thức lượng trong tam giác vuông, ta có:
![]() (với x > 0)
(với x > 0)
![]()
![]() (với y> 0)
(với y> 0)
![]()
Vậy ![]()
Bài 3 (trang 69 SGK Toán 9 Tập 1)
Hãy tính x và y trong mỗi hình sau: (h.6)
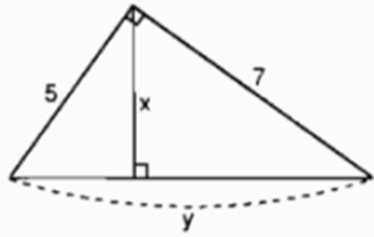
Gợi ý đáp án
Xét ![]() vuông tại A. Theo định lí Pytago, ta có:
vuông tại A. Theo định lí Pytago, ta có:
![]()
![]()
![]()
Áp dụng hệ thức liên quan đến đường cao trong tam giác vuông, ta có:
![]()
![]()
![]()
![]()
![]()
Vậy ![]()
Bài 4 (trang 69 SGK Toán 9 Tập 1)
Hãy tính x và y trong mỗi hình sau: (h.7)
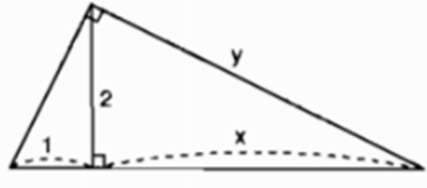
Gợi ý đáp án
Theo định lí 2 ta có:
22 = 1.x => x = 4
Theo định lí 1 ta có:
y2 = x(1 + x) = 4(1 + 4) = 20
=> y = √20 = 2√5
III. Giải bài tập toán 9 trang 69, 70 tập 1: Luyện tập
Bài 5 (trang 69 SGK Toán 9 Tập 1)
Trong tam giác vuông với các cạnh góc vuông có độ dài 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.
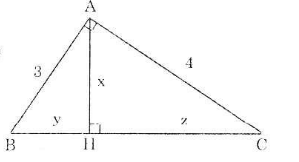
Gợi ý đáp án
Xét ![]() vuông tại A, đường cao AH có AB=3, AC=4. Ta cần tính AH, BH và CH.
vuông tại A, đường cao AH có AB=3, AC=4. Ta cần tính AH, BH và CH.
Áp dụng định lí Pytago cho ![]() vuông tại A, ta có:
vuông tại A, ta có:
![]()
![]()
![]()
Xét ![]() vuông tại A, đường cao AH. Áp dụng các hệ thức lượng trong tam giác vuông, ta được:
vuông tại A, đường cao AH. Áp dụng các hệ thức lượng trong tam giác vuông, ta được:
*![]()
![]()
![]()
![]()
Bài 6 (trang 69 SGK Toán 9 Tập 1)
Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.
Gợi ý đáp án
ΔABC vuông tại A và đường cao AH như trên hình.
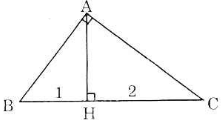
BC = BH + HC = 1 + 2 = 3
Theo định lí 1: AB2 = BH.BC = 1.3 = 3
=> AB = √3
Theo định lí 1: AC2 = HC.BC = 2.3 = 6
=> AC = √6
Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.
Bài 7 (trang 69 SGK Toán 9 Tập 1)
Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x2 = ab) như trong hai hình sau:
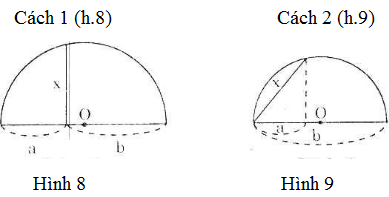
Theo cách dựng, ΔABC có đường trung tuyến AO bằng một nửa cạnh BC, do đó ΔABC vuông tại A.

Vì vậy AH2 = BH.CH hay x2 = ab
Đây chính là hệ thức (2) hay cách vẽ trên là đúng.
Bài 8 (trang 70 SGK Toán 9 Tập 1)
Tìm x và y trong mỗi hình sau:

Gợi ý đáp án
Đặt tên các điểm như hình vẽ:
Xét ![]() vuông tại A, đường cao AH. Áp dụng hệ thức
vuông tại A, đường cao AH. Áp dụng hệ thức ![]() , ta được:
, ta được:
![]()
Vậy x=6
b) Đặt tên các điểm như hình vẽ
Xét ![]() vuông tại D, đường cao DH. Áp dụng hệ thức
vuông tại D, đường cao DH. Áp dụng hệ thức ![]() , ta được:
, ta được:
![]()
![]()
Xét ![]() vuông tại H. Áp dụng định lí Pytago, ta có:
vuông tại H. Áp dụng định lí Pytago, ta có:
![]()
![]()
Vậy ![]()
c) Đặt tên các điểm như hình vẽ:
Xét ![]() vuông tại P, đường cao PH. Áp dụng hệ thức
vuông tại P, đường cao PH. Áp dụng hệ thức ![]() ', ta được:
', ta được:
![]()
Xét ![]() vuông tại H. Áp dụng định lí Pytago, ta có:
vuông tại H. Áp dụng định lí Pytago, ta có:
![]()
Vậy x=9, y=15.
Bài 9 (trang 70 SGK Toán 9 Tập 1)
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng ![]()
Gợi ý đáp án
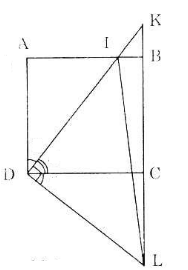
a) Xét ![]() có:
có:
![]()
AD=CD (hai cạnh hình vuông)
![]()
Do đó ![]() (g.c.g)
(g.c.g)
Suy ra DI=DL.
Vậy ![]() cân (đpcm).
cân (đpcm).
b) Xét ![]() vuông tại D, đường cao DC.
vuông tại D, đường cao DC.
Áp dụng hệ thức ![]() , ta có:
, ta có:
![]() (mà DL=DI)
(mà DL=DI)
Suy ra ![]()
Do DC không đổi nên ![]() là không đổi.
là không đổi.
Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức ![]()
Nếu đề bài không cho vẽ ![]() thì ta vẫn phải vẽ đường phụ
thì ta vẫn phải vẽ đường phụ ![]() để có thể vận dụng hệ thức trên.
để có thể vận dụng hệ thức trên.
IV. Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông
I. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
* Phát biểu: Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
* Bài toán: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng ![]() và
và ![]()
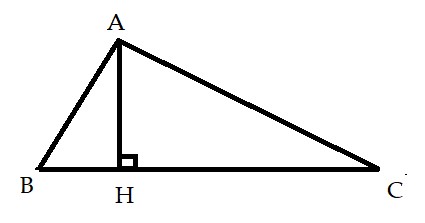
→ Chứng minh:
+ Xét ![]() và
và ![]() có:
có:
![]() chung
chung
![]()
Suy ra ![]() (g.g)
(g.g) ![]() (cặp cạnh tương ứng tỉ lệ)
(cặp cạnh tương ứng tỉ lệ)
![]() (đpcm)
(đpcm)
II. Một số hệ thức liên quan tới đường cao
1. Định lí 1
* Phát biểu: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
* Bài toán: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng :![]()
→ Chứng minh:
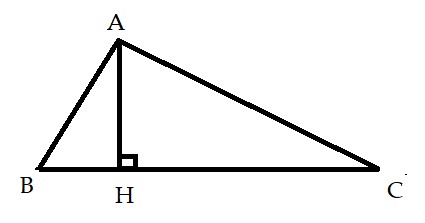
+ Xét ![]() và
và ![]() có:
có:
![]() chung
chung
![]()
Suy ra ![]() (g.g)
(g.g) ![]() (cặp góc tương ứng tỉ lệ)
(cặp góc tương ứng tỉ lệ)
+ Xét ![]() và
và ![]() có:
có:
![]() (cmt)
(cmt)
![]()
Suy ra ![]() (g.g)
(g.g) ![]() (cặp cạnh tương ứng tỉ lệ)
(cặp cạnh tương ứng tỉ lệ)
(đpcm)
![]()
2. Định lý 2
* Phát biểu: Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
* Bài toán: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng ![]()
→ Chứng minh:
+ Xét tam giác ABC vuông tại A, đường cao AH có:
![]() (đpcm)
(đpcm)
3. Định lý 3
* Phát biểu: Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
* Bài toán: Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh rằng ![]()
→ Chứng minh:
+ Xét tam giác ABC vuông tại A, đường cao AH có:
![]()
![]()
![]() (đpcm)
(đpcm)
!Ví dụ: Cho tam giác ABC vuông tại A, có AB = 6cm và AC = 8cm và đường cao AH. Tính BC, AH, BH và HC.
+ Xét tam giác ABC vuông tại A, đường cao AH có:
 (Pytago)
(Pytago)
Thay số tính được BC = 10 (cm)
 (hệ thức lượng trong tam giác vuông)
(hệ thức lượng trong tam giác vuông)
Thay số tính được AH = ![]() (cm)
(cm)
- ·
 (hệ thức lượng trong tam giác vuông)
(hệ thức lượng trong tam giác vuông)
Thay số tính được BH = ![]() (cm)
(cm)
- ·
 (hệ thức lượng trong tam giác vuông)
(hệ thức lượng trong tam giác vuông)
Thay số tính được HC = ![]() (cm)
(cm)
