Giải Toán lớp 9 trang 44, 45 tập 1 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi và bài tập trong SGK bài 1 Nhắc lại và bổ sung các khái niệm về hàm số thuộc chương 2 Đại số.
Giải Toán 9 Bài 2 Chương 2 Đại số được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 44, 45 tập 1 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.
Giải Toán 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
Trả lời câu hỏi Toán 9 Bài 1
Câu hỏi 1
Cho hàm số y = f(x) = 1/2x + 5.
Tính f(0); f(2); f(3); f(-2); f(-10).
Gợi ý đáp án
f(0) = 1/2.0 + 5 = 5
f(2) = 1/2.2 + 5 = 6
f(3) = 1/2.3 + 5 = 13/2
f(-2) = 1/2.(-2) + 5 = 4
f(-10) = 1/2.(-10) + 5 = 0
Câu hỏi 2
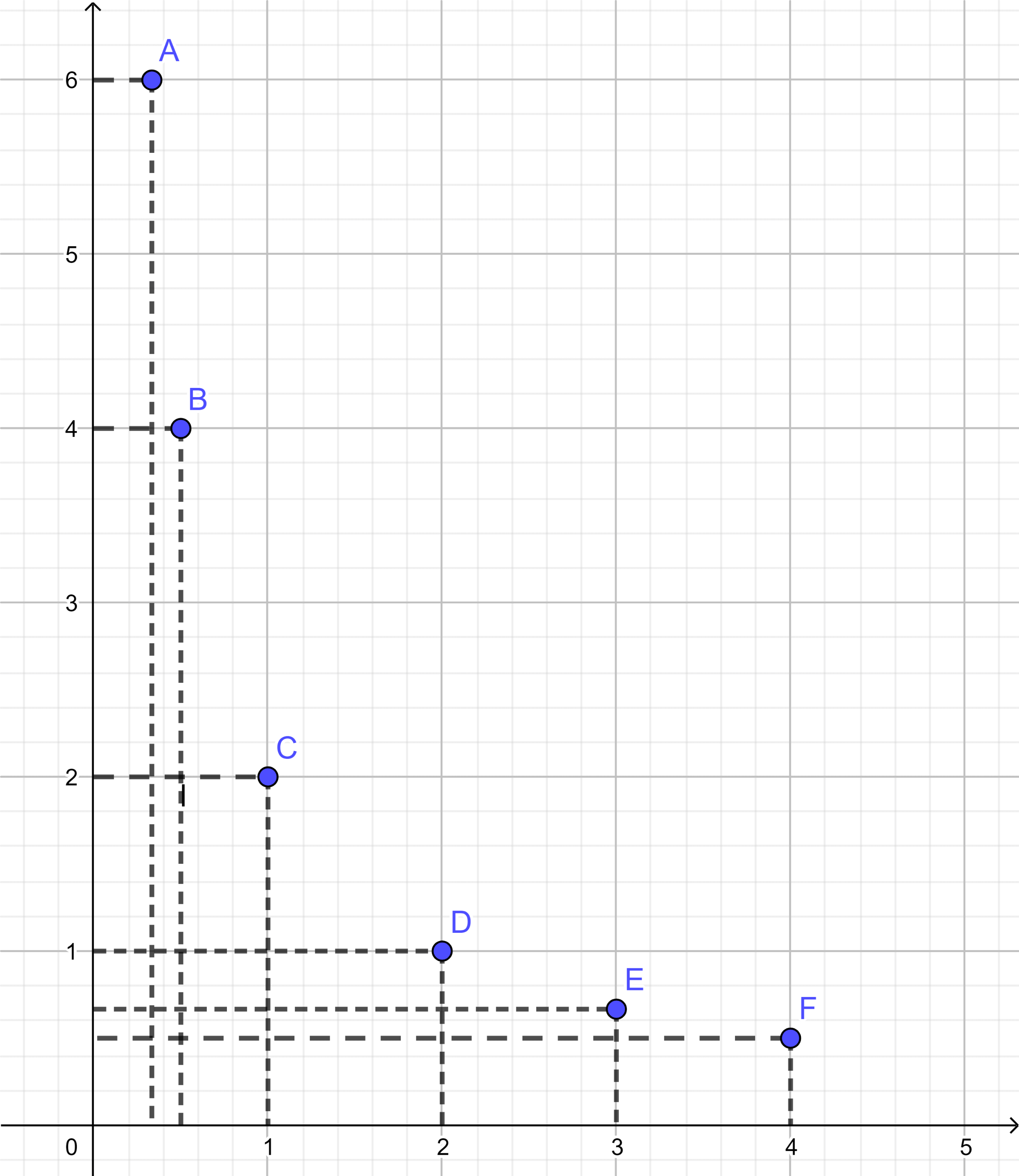
a) Biểu diễn các điểm sau trên mặt phẳng tọa độ Oxy:
A(1/3; 6), B(1/2; 4), C(1; 2), D(2; 1), E(3; 2/3), F(4; 1/2).
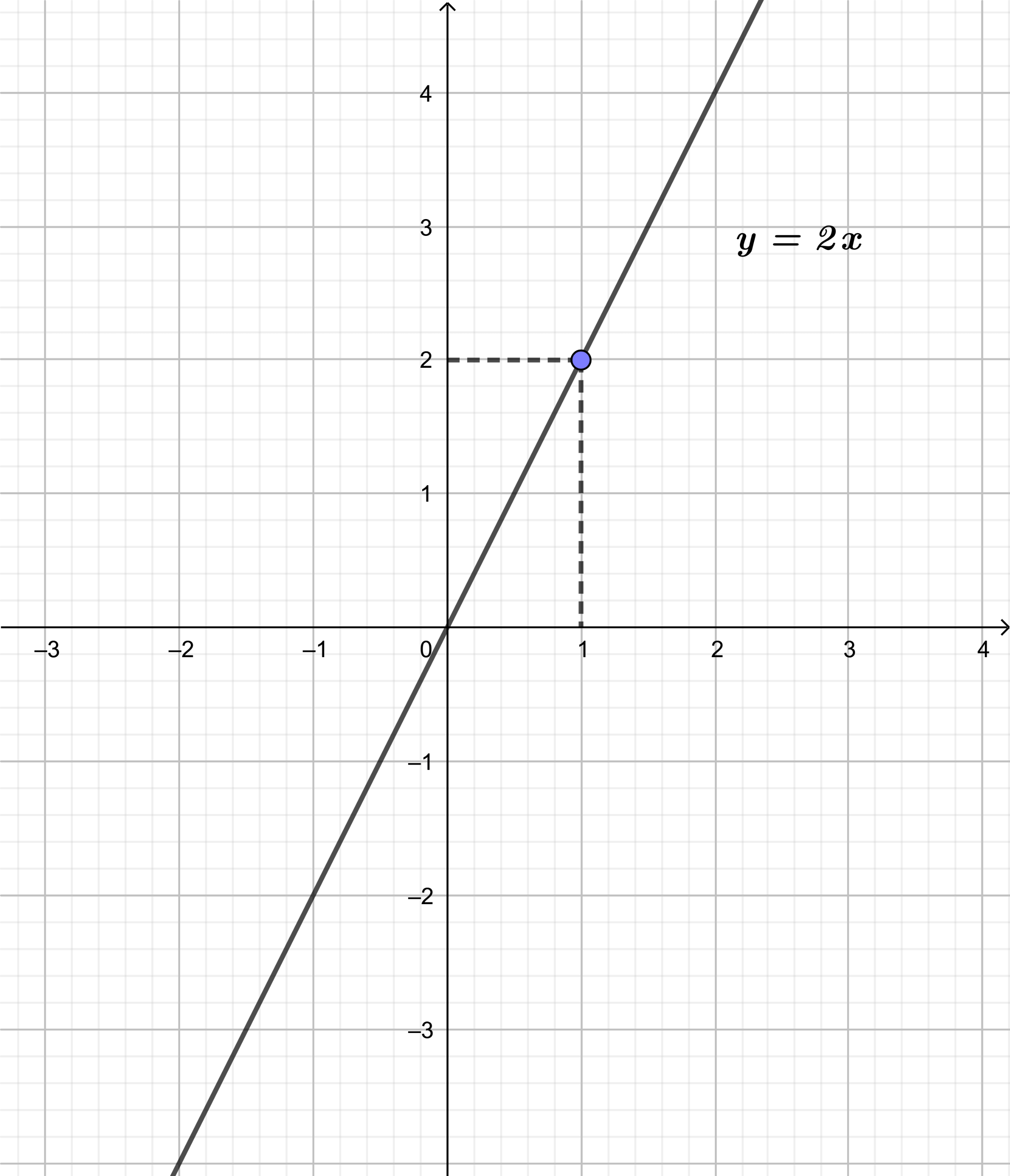
b) Vẽ đồ thị của hàm số y = 2x.
Gợi ý đáp án
Ta có hình vẽ sau:
Bảng giá trị
x | 0 | 1 |
y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua 2 điểm (0; 0) và (1; 2)
Giải bài tập Toán 9 trang 44, 45 tập 1
Bài 1
a) Cho hàm số ![]()
Tính: ![]()
b) Cho hàm số ![]()
Tính: ![]()
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị ?
Gợi ý đáp án
a) Thay các giá trị vào hàm số ![]() . Ta có
. Ta có
![]()
![]()
![]()
![]()
![]()
![]()
![]()
b) Thay các giá trị vào hàm số ![]() . Ta có
. Ta có
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
c)
Từ kết quả câu a và câu b ta thấy:
Khi x lấy cùng một giá trị thì giá trị của g(x) lớn hơn giá trị của f(x) là 3 đơn vị.
(Chú ý: Hai hàm số![]() và
và ![]() đều là hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên).
đều là hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên).
Bài 2
Đề bài
Cho hàm số ![]()
a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:

b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?
Gợi ý đáp án
a) Ta có ![]()
Với ![]() thay các giá trị của x vào biểu thức của y, ta được:
thay các giá trị của x vào biểu thức của y, ta được:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ta có bảng sau:

b) Nhìn vào bảng giá trị của hàm số ở câu a ta thấy khi x càng tăng thì giá trị của f(x) càng giảm. Do đó hàm số nghịch biến trên R.
Bài 3
Giải bài 3 trang 45 SGK Toán 9 tập 1. Cho hai hàm số y = 2x và y = -2x.
Đề bài
Cho hai hàm số y = 2x và y = -2x
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
Gợi ý đáp án
a) - Với hàm số y = 2x
Bảng giá trị:
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)
- Với hàm số y = -2x
Bảng giá trị:
| x | 0 | 1 |
| y = -2x | 0 | -2 |
Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B( 1; - 2)

b) - Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2).
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3).
Vậy hàm số y = -2x nghịch biến trên R.
Giải bài tập Toán 9 trang 45, 46 tập 1: Luyện tập
Bài 4
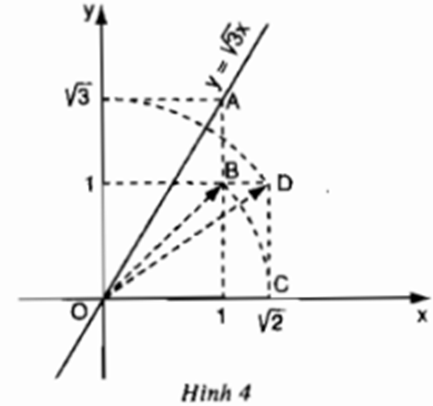
Đồ thị hàm số y = √3 x được vẽ bằng compa và thước thẳng ở hình 4. Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
Gợi ý đáp án
Cách vẽ:
- Cho x=1 ta được ![]() . Suy ra
. Suy ra ![]()
- Cho x=0 ta được ![]() . Suy ra O(0;0)
. Suy ra O(0;0)
Vẽ đường thẳng qua O, A được đồ thị hàm số ![]()
Các bước vẽ:
- Vẽ một hình vuông có độ dài cạnh là 1 đơn vị, có một đỉnh là O, lấy điểm B(1;1). Khi đó, đường chéo OB có độ dài bằng ![]()
- Vẽ cung tròn tâm O, bán kính OB , ta xác định được điểm C trên tia Ox, và ta có ![]() .
.
- Vẽ một hình chữ nhật có một đỉnh là O, cạnh CD = 1 và cạnh ![]() ta được đường chéo
ta được đường chéo ![]()
- Vẽ cung tròn tâm O, bán kính OD , ta xác định được điểm E trên tia Oy, và ta có ![]() .
.
- Vẽ hình chữ nhật có một đỉnh là O, có một cạnh bằng 1 đơn vị và một cạnh có độ dài bằng ![]() ta được điểm
ta được điểm ![]() .
.
- Vẽ đường thẳng đi qua gốc tọa độ O và điểm A ta được đồ thị của hàm số ![]()
Bài 5
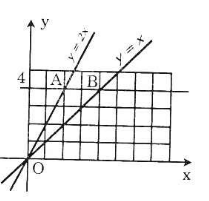
a) Vẽ đồ thị của các hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy (hình 5).
b) Đường thẳng song song với trục Ox và cắt trục Oy tại các điểm có tung độ y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.
Tìm tọa độ các điểm A, B, tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimet
Gợi ý đáp án
a. Vẽ đồ thị

b) - Từ hình vẽ ta có: yA = yB = 4 suy ra:.
+ Hoành độ của A: 4 = 2.xA => xA = 2 (*)
+ Hoành độ của B: 4 = xB => xB = 4
=> Tọa độ 2 điểm là: A(2, 4); B(4, 4)
- Tìm độ dài các cạnh của ΔOAB
Dễ thấy AB = 4 - 2 = 2 (cm).
Gọi C là điểm biểu diễn số 4 trên trục tung, ta có OC=4cm,AC=2cm;BC=4cm
Áp dụng định lý Py-ta-go cho các tam giác vuông OAC và OBC, ta có:

![]()
![]()
![]()
+) Tính diện tích ∆OAB:
Cách 1:

Cách 2:
∆OAB có đường cao ứng với cạnh AB là OC.
![]()
Bài 6
Cho các hàm số y = 0,5x và y = 0,5x + 2.
a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:
| x | -2,5 | -2,25 | -1,5 | -1 | 0 | 1 | 1,5 | 2,25 | 2,5 |
| y = 0,5x | |||||||||
| y = 0,5x + 2 |
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số đó khi biến x lấy cùng một giá trị?
Gợi ý đáp án
a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:
| x | -2,5 | -2,25 | -1,5 | -1 | 0 | 1 | 1,5 | 2,25 | 2,5 |
| y = 0,5x | -1,25 | -1,125 | -0,75 | -0,5 | 0 | 0,5 | 0,75 | 1,125 | 1,25 |
| y = 0,5x + 2 | 0,75 | 0,875 | 1,25 | 1,5 | 2 | 2,5 | 2,75 | 3,125 | 3,25 |
b) Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là 2 đơn vị.
Lý thuyết Nhắc lại và bổ sung các khái niệm về hàm số
A. Tóm tắt kiến thức:
1. Định nghĩa hàm số:
Nếu đại lượng y phụ thuộc vào một đại lượng thay đổi sao cho với mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x được gọi là biến số.
Hàm số thường được kí hiệu bởi những chữ f, g, h... chẳng hạn khi y là một hàm số của biến số x, ta viết y = f(x) hoặc y = g(x),…
- f(a) là giá trị của hàm số y = f(x) tại x = a.
Khi hàm số y được cho bởi công thức y = f(x), muốn tính giá trị f(a) của hàm số tại x = a, ta thay x = a vào biểu thức f(x) rồi thực hiện các phép tính trong biểu thức.
- Khi x thay đổi mà y luôn nhận một giá trị không đổi thì y được gọi là một hàm hằng.
2. Đồ thị của hàm số:
Tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ được gọi là đồ thị của hàm số y = f(x).
3. Hàm số đồng biến, hàm số nghịch biến:
Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc tập số thực R. Với x1, x2 tùy ý thuộc R:
a) Nếu x1< x2 mà f(x1) < f(x2) thì hàm số được gọi là hàm đồng biến.
b) Nếu x1< x2 mà f(x1) > f(x2) thì hàm số được gọi là hàm nghịch biến.
