Download.vn mời quý thầy cô cùng tham khảo tài liệu Giải bài tập SGK Toán 9 Tập 2 trang 36, 36 để xem gợi ý giải các bài tập của Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0) thuộc chương 4 Đại số 9.
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa trang 36, 37 Toán lớp 9 tập 2. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 2 Chương 4 trong sách giáo khoa Toán 9 Tập 2. Chúc các bạn học tốt.
Giải Toán 9 Bài 2: Đồ thị của hàm số y = ax2 (a ≠ 0)
Lý thuyết Đồ thị của hàm số y = ax2 (a ≠ 0)
1. Đồ thị hàm số y = ax2 (a ≠0)
Đồ thị của hàm số y = ax2 (a ≠0) là một đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong đó được gọi là một parabol với đỉnh O.
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất cảu đồ thị.
2. Cách vẽ đồ thị hàm số y = ax2 (a ≠0)
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
Bước 3: Vẽ đồ thị và kết luận.
3. Ví dụ cụ thể
Câu 1: Vẽ đồ thị hàm số y = x2.
Tập xác định: x ∈ R
Bảng giá trị tương ứng của x và y
| x | 0 | 1 | -1 | 2 | -2 |
| y = x2 | 0 | 1 | 1 | 4 | 4 |
Đồ thị :
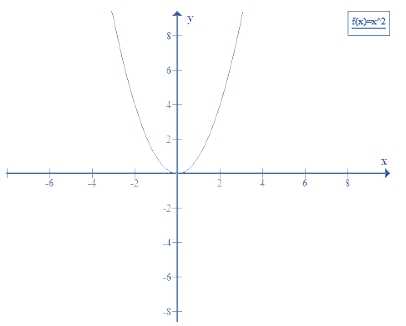
Giải bài tập toán 9 trang 36, 37 tập 2
Bài 4 (trang 36 SGK Toán 9 Tập 2)
Cho hai hàm số: ![]() Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
| x | -2 | -1 | 0 | 1 | 2 |
| x | -2 | -1 | 0 | 1 | 2 |
Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.
Thực hiện phép tính sau:
+) Đối với hàm số ![]()
![]()
![]()
![]()
![]()
![]()
+) Đối với hàm số ![]()
![]()
![]()
![]()
![]()
![]()
Ta được bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| 6 | 0 | 6 | |||
| 6 | 0 | - 6 |
Vẽ đồ thị:
+) Vẽ đồ thị hàm số ![]()
Quan sát bảng trên ta thấy đồ thị đi qua các điểm:
![]()
+) Vẽ đồ thị hàm số ![]()
Quan sát bảng trên ta thấy đồ thị đi qua các điểm:
![]()
![]()
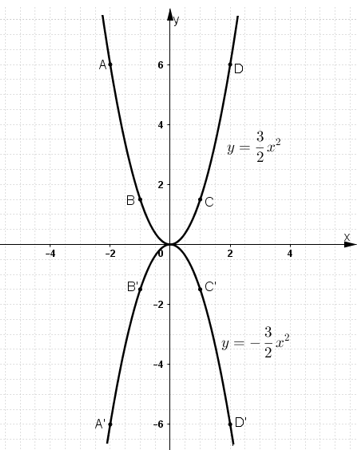
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox
Bài 5 (trang 37 SGK Toán 9 Tập 2)
Cho ba hàm số:
![]()
a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.
c) Tìm ba điểm A’ ; B’ ; C’ có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A’ ; B và B’ ; C và C’.
d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.
a) +) Vẽ đồ thị hàm số ![]()
Cho ![]() . Đồ thị đi qua
. Đồ thị đi qua ![]()
Cho ![]() . Đồ thị đi qua
. Đồ thị đi qua ![]()
Cho ![]() . Đồ thị hàm số đi qua điểm (2; 2).
. Đồ thị hàm số đi qua điểm (2; 2).
Cho ![]() Đồ thị hàm số đi qua điểm (-2; 2).
Đồ thị hàm số đi qua điểm (-2; 2).
Đồ thị hàm số ![]() là parabol đi qua gốc tọa độ và các điểm trên.
là parabol đi qua gốc tọa độ và các điểm trên.
+) Vẽ đồ thị hàm số y=x2
Cho x=1 ⇒ y=1. Đồ thị đi qua (1; 1).
Cho ![]() . Đồ thị đi qua (-1; 1).
. Đồ thị đi qua (-1; 1).
Cho ![]() . Đồ thị hàm số đi qua điểm (2; 4).
. Đồ thị hàm số đi qua điểm (2; 4).
Cho ![]() Đồ thị hàm số đi qua điểm (-2; 4).
Đồ thị hàm số đi qua điểm (-2; 4).
Đồ thị hàm số y=x2 là parabol đi qua gốc tọa độ và các điểm trên.
+) Vẽ đồ thị hàm số y=2x2.
Cho x=1 ⇒ y=2.1x2 =2. Đồ thị đi qua (1; 2).
Cho x=-1 ⇒ y=2.(-1)x2. Đồ thị đi qua (-1; 2).
Cho x=2 ⇒ y=2.2x2=8. Đồ thị hàm số đi qua điểm (2; 8).
Cho x=-2 ⇒ y=2.(-2)x2=8. Đồ thị hàm số đi qua điểm (-2; 8).
Đồ thị hàm số y=2xx2 là parabol đi qua gốc tọa độ và các điểm trên.
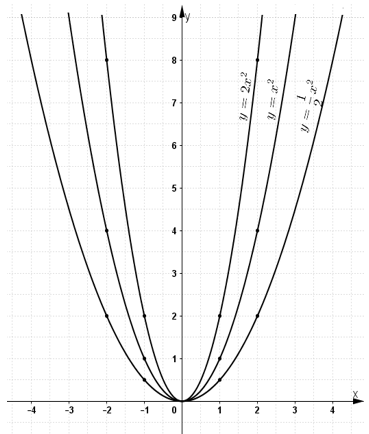
b)
Xác định điểm P trên trục Ox có hoành độ x = - 1,5. Qua P kẻ đường thẳng song song với trục Oy, nó cắt các đồ thị ![]() lần lượt tại A;B;C
lần lượt tại A;B;C
Gọi ![]() lần lượt là tung độ các điểm A, B, C. Ta có:
lần lượt là tung độ các điểm A, B, C. Ta có:

c) Xác định điểm P' trên trục Ox có hoành độ x = 1,5. Qua P' kẻ đường thẳng song song với trục Oy, nó cắt các đồ thị ![]() lần lượt tại A';B';C'
lần lượt tại A';B';C'
Gọi ![]() lần lượt là tung độ các điểm A', B', C' . Ta có:
lần lượt là tung độ các điểm A', B', C' . Ta có:

Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị.
Vậy với x = 0 thì các hàm số trên đều có giá trị nhỏ nhất y=0.
