Giải bài tập SGK Toán 9 Tập 1 trang 119 để xem gợi ý giải các bài tập của Bài 7: Vị trí tương đối của hai đường tròn thuộc chương 2 Hình học 9.

Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa Toán lớp 9 tập 1 trang 119. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài Vị trí tương đối của hai đường tròn Chương 2 trong sách giáo khoa Toán 9 Tập 1. Chúc các bạn học tốt.

Lý thuyết Vị trí tương đối của hai đường tròn

1. Ba vị trí tương đối của hai đường tròn.

a) Hai đường tròn cắt nhau.

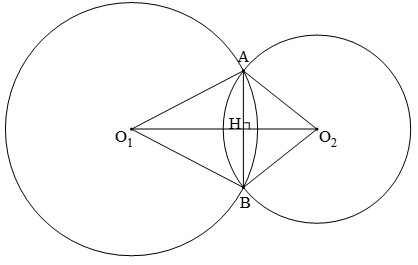
Hai đường tròn có hai điểm chung được gọi là hai đường tròn cắt nhau.

+ Hai điểm A, B là hai giao điểm.

+ Đoạn thẳng AB là dây chung.

+ Đặt O₁A = R; O₂A = r khi đó: |R - r| < O₁O₂ < R + r

+ Đường thẳng O₁O₂ là đường nối tâm, đoạn thẳng O₁O₂ là đoạn nối tâm.

+ Tính chất đường nối tâm: Đường nối tâm là đường trung trực của dây chung

b) Hai đường tròn tiếp xúc nhau.

Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn tiếp xúc.

+ Điểm A gọi là tiếp điểm.

+ Có hai trường hợp tiếp xúc của hai đường tròn:

⋅ Tiếp xúc ngoài tại A: O₁O₂ = R + r

⋅ Tiếp xúc trong tại A: O₁O₂ = |R - r|

c) Hai đường tròn không giao nhau

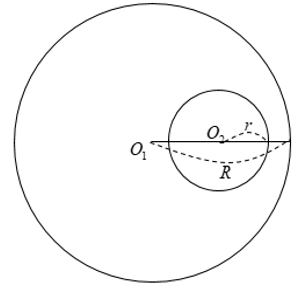
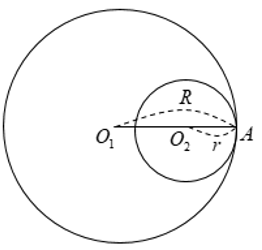
Hai đường tròn không có điểm chung nào được gọi là hai đường tròn không giao nhau.

+ Hai đường tròn ngoài nhau: O₁O₂ > R + r

+ Hai đường tròn đựng nhau: O₁O₂ < |R - r|

+ Đặc biệt, khi (O₁) và (O₂) đồng tâm: O₁O₂ = 0

2. Định lý

+ Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây cung.

+ Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.

Giải bài tập toán 9 trang 119 tập 1

Bài 33 (trang 119 SGK Toán 9 Tập 1)

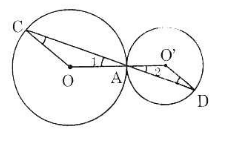
Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O'D.

Gợi ý đáp án

Vì (O) và (O’) tiếp xúc nhau tại A (gt) ⇒ O,A, O’ thẳng hàng.

Xét  có OC = OA (= bán kính (O) nên tam giác OCA cân tại O.

Tương tự ta có tam giác O'AD cân tại O' (do O'A=O'D= bán kính (O') suy ra

Lại có (đối đỉnh) (3)

Từ (1), (2) và (3) suy ra mà góc và so le trong, do đó OC // O’D (đpcm)

Bài 34 (trang 119 SGK Toán 9 Tập 1)

Cho hai đường tròn (O; 20cm) và (O'; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng AB = 24 cm. (Xét hai trường hợp: O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB).

Gợi ý đáp án

* TH1: O và O' nằm khác phía đối với AB (h.a)

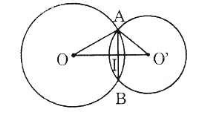
Vẽ dây cung AB cắt OO' tại H. Theo định lí - trang 119 về tính chất đường nối tâm, ta có: và cm.

Xét tam giác AOH vuông tại H, áp dụng định lí Pytago, ta có:

Xét tam giác AO'H vuông tại H, áp dụng định lí Pytago, ta có:

Khi đó OO'=OH+HO'=16+9=25(cm).

*TH2: O và O' nằm cùng phía đối với AB (h.b)

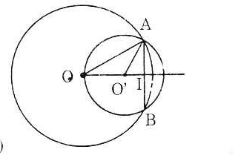
Tương tự TH1 ta vẫn có OH=16cm;O'H=9cm

Khi đó OO'=OH-O'H=16-9=7(cm).