Giải Toán 9 trang 103, 104, 105

Giải Toán lớp 9 trang 103, 104, 105 tập 2 giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các bài tập trong SGK Bài Ôn tập Chương III: Góc với đường tròn.

Giải Toán 9 Ôn tập Chương III: Góc với đường tròn được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán. Giải Toán lớp 9 trang 103, 104, 105 tập 2 là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn.

Giải Toán 9: Ôn tập Chương III: Góc với đường tròn

Giải Toán 9 trang 103, 104, 105 tập 2

Giải Toán 9 trang 103, 104, 105 tập 2

Bài 88

Hãy nêu tên mỗi góc trong các hình dưới đây:

(Ví dụ. góc trên hình 66b) là góc nội tiếp).

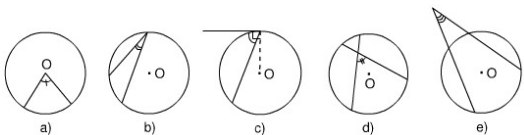
Gợi ý đáp án:

a) Góc ở tâm.

b) Góc nội tiếp.

c) Góc tạo bởi tiếp tuyến và dây cung.

d) Góc có đỉnh bên trong đường tròn.

e) Góc có đỉnh bên ngoài đường tròn.

Bài 89

Trong hình 67, cung AmB có số đo là 60o. Hãy:

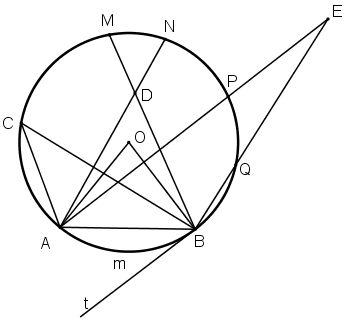a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.

b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.

c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.

d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn.

d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh $\widehat {A{\rm{D}}B}$ với $\widehat {ACB} .$

e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh $\widehat {A{\rm{E}}B}$ với $\widehat {ACB}$

Gợi ý đáp án:

a) Từ O nối với hai đầu mút của cung AB

Ta có $\widehat {AOB}$ là góc ở tâm chắn cung AB

Vì $\widehat {AOB}$ là góc ở tân chắn cung AB nên

$\widehat {AOB} =sđ\overparen{AmB}=60^0$

b) Lấy một điểm C bất kì trên (O). Nối C với hai đầu mút của cung AmB. Ta được góc nội tiếp $\widehat {ACB}$

Khi đó: $\displaystyle \widehat {ACB} = {1 \over 2}sđ\overparen{AmB}={1 \over 2}{60^0} = 30$

c) Vẽ bán kính OB. Qua B vẽ Bt\bot OB. Ta được góc ABt là góc tạo bởi tia tiếp tuyến Bt với dây cung BA.

Ta có: $\displaystyle \widehat {ABt} = {1 \over 2}sđ\overparen{AmB} = {30^0}$

d) Lấy điểm D bất kì ở bên trong đường tròn (O). Nối D với A và D với B, ta được góc ADB là góc có đỉnh ở bên trong đường tròn (O)

Đường thẳng AD cắt đường tròn tại điểm thứ hai là K, DB cắt đường tròn tại điểm thứ hai là C.

Ta có:

$\eqalign{ & \widehat {ACB} = {1 \over 2}sđ\overparen{AmB}\cr & \widehat {A{\rm{D}}B} = {1 \over 2}\left( sđ\overparen{AmB}+ sđ\overparen{CK} \right) \cr}$

Mà $sđ\overparen{AmB}+sđ\overparen{CK}>sđ\overparen{AmB}(do sđ\overparen{CK}>0)$ nên $\widehat {A{\rm{D}}B} > \widehat {ACB}$

e) Lấy điểm E bất kì ở bên ngoài đường tròn, nối E với A và E với B, chúng cắt đường tròn lần lượt tại J và I.

Ta có góc AEB là góc ở bên ngoài đường tròn (O)

Có:

$\eqalign{ & \widehat {ACB} = {1 \over 2}sđ\overparen{AmB} \cr & \widehat {A{\rm{E}}B} = {1 \over 2}\left( sđ\overparen{AmB} - sđ\overparen{IJ} \right) \cr}$

Mà $sđ\overparen{AmB}– sđ \overparen{IJ}< sđ\overparen{AmB} (do sđ\overparen{IJ}> 0)$

Nên $\widehat {A{\rm{E}}B} < \widehat {ACB}.$

Bài 90

a) Vẽ hình vuông cạnh 4cm.

b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.

c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.

Gợi ý đáp án:

a) Dùng êke ta vẽ hình vuông ABCD có cạnh bằng 4cm như sau:

- Vẽ AB = 4cm.

- Vẽ $BC \bot AB$ và BC = 4cm

- Vẽ $DC\bot BC$ và DC = 4cm

-Nối D với A, ta có $AD\bot DC$ và AD = 4cm

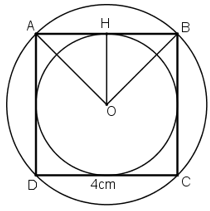
b) Ta có ABCD là hình vuông. Gọi O là giao điểm của 2 đường chéo AC và BD khi đó ta có: OA = OB = OC = OD. Nên O chính là tâm của đường tròn ngoại tiếp hình vuông.

Tam giác ABC là tam giác vuông cân nên AB = BC.

Áp dụng định lí Pytago trong tam giác vuông ABC, ta có:

$\eqalign{ & A{C^2} = A{B^2} + B{C^2} = 2{\rm{A}}{B^2} \Leftrightarrow A{C^2} = {2.4^2} = 32 \cr & \Rightarrow AC = \sqrt {32} = 4\sqrt 2 \cr}$

Vậy $\displaystyle AO = R = {{AC} \over 2} = {{4\sqrt 2 } \over 2} = 2\sqrt 2$

Vậy $R = 2\sqrt{2}$ cm

c) Vẽ $OH \bot DC$ .Tương tự ta kẻ từ O các đường vuông góc đến các cạnh AD, AB, BC. Khi đó ta có

Đường tròn tâm O, bán kính OH. Đó là đường tròn nội tiếp hình vuông ABCD

Ta có: $\displaystyle OH = {{A{\rm{D}}} \over 2} = 2$ (cm)

Vậy r = OH = 2cm

Bài 91

Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.

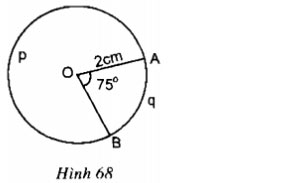
a) Tính số đo cung ApB.

b) Tính độ dài hai cung AqB và ApB.

c) Tính diện tích hình quạt tròn OAqB

Gợi ý đáp án:

a) Ta có $\widehat {AOB}$ là góc ở tâm chắn cung AqB nên:

$\widehat {AOB} = sđ\overparen{AqB}$ hay $sđ\overparen{AqB}=75^0$

Vậy $sđ\overparen{ApB} =360°- \overparen{AqB} =360^0 - 75^0 = 285^0$

b) ${l_{\overparen{AqB}}}$ là độ dài cung AqB, ta có:

$\displaystyle {l_{\overparen{AqB}}} =\displaystyle {{\pi Rn} \over {180}} = {{\pi .2.75} \over {180}} = {5 \over 6}\pi$ (cm)

Gọi ${l_{\overparen{ApB}}}$ là độ dài cung ApB ta có:

$\displaystyle {l_{\overparen{ApB}}}= {{\pi Rn} \over {180}} = {{\pi .2.285} \over {180}} = {{19\pi } \over 6}$ (cm)

c) Diện tích hình quạt tròn OAqB là:

$\displaystyle {S_{OAqB}} = {{\pi {R^2}n} \over {360}} = {{\pi {2^2}.75} \over {360}} = {{5\pi } \over 6}(c{m^2})$

Bài 92

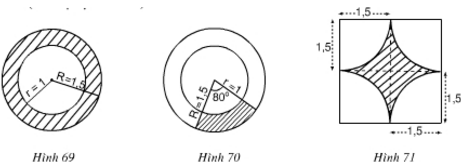
Hãy tính diện tích miền gạch sọc trong các hình 69, 70, 71 (đơn vị độ dài: cm).

Gợi ý đáp án:

a) Hình 69

Diện tích hình tròn bán kính R= 1,5 là: ${S_1} = πR^2 = π. 1,5^2 = 2,25π$

Diện tích hình tròn bán kính r = 1 là: ${S_2} = πr^2= π. 1^2 = π$

Vậy diện tích miền gạch sọc là:

$S = {S_1} – {S_2} = 2,25 π – π = 1,25 π$ (đvdt)

b) Hình 70

Diện tích hình quạt có bán kính $R = 1,5; n^0 = 80^0$

$\displaystyle {S_1} = {{\pi {R^2}n} \over {360}} = {{\pi 1,{5^2}.80} \over {360}} = {\pi \over 2}$

Diện tích hình quạt có bán kính $r = 1; n^0 = 80^0$

$\displaystyle {S_2} = {{\pi {r^2}n} \over {360}} = {{\pi {{.1}^2}.80} \over {360}} = {{2\pi } \over 9}$

Vậy diện tích miền gạch sọc là: $\displaystyle S = {S_1} - {S_2} = {\pi \over 2} - {{2\pi } \over 9} = {{9\pi - 4\pi } \over {18}} = {{5\pi } \over {18}}$

* Hình c

Dựa vào hình vẽ,diện tích phần gạch sọc bằng diện tích hình vuông trừ đi bốn phần diện tích hình quạt ở bốn góc ( Mỗi hình quạt tương ứng 1/4 hình tròn bán kính 1,5 cm. Do đó, tổng 4 phần tương ứng với diện tích của một hình tròn bán kính 1,5 cm )

Hình vuông có độ dài cạnh 3 cm nên có diện tích là: S = 3² = 9 ( cm2).

Hình tròn có bán kính là R= 1,5 cm nên diện tích hình tròn là:

s= π.1,5² cm²

Diện tích phần gạch sọc là: Ssọc= S – s = 9- π.1,5²≈ 1, 94 cm²

Bài 93

Có ba bánh xe răng cưa A, B, C cùng chuyển động ăn khớp với nhau. Khi một bánh xe quay thì hai bánh xe còn lại cũng quay theo. Bánh xe A có 60 răng, bánh xe B có 40 răng, bánh xe C có 20 răng. Biết bán kính bánh xe C là 1cm. Hỏi:

a) Khi bánh xe C quay 60 vòng thì bánh xe B quay mấy vòng?

b) Khi bánh xe A quay 80 vòng thì bánh xe B quay mấy vòng?

c) Bán kính của các bánh xe A và B là bao nhiêu?

Hướng dẫn giải

- Chu vi vòng tròn: C = 2π R

Gợi ý đáp án:

Ta có bánh xe A có 60 răng, bánh xe B có 40 răng, bánh xe C có 20 răng nên suy ra chu vi của bánh xe B gấp đôi chu vi bánh xe C, chu vi bánh xe A gấp ba chu vi bánh xe C.

Chu vi bánh xe C là: 2. 3,14 . 1 = 6,28 (cm)

Chu vi bánh xe B là: 6,28 . 2 = 12,56 (cm)

Chu vi bánh xe A là: 6,28 . 3 = 18,84 (cm)

a) Khi bánh xe C quay được 60 vòng thì quãng đường đi được là:

60 . 6,28 = 376,8 (cm)

Khi đó số vòng quay của bánh xe B là:

376,8 : 12,56 = 30 (vòng)

b) Khi bánh xe A quay được 80 vòng thì quãng đường đi được là:

80 . 18,84 = 1507,2 (cm)

Khi đó số vòng quay của bánh xe B là:

1507,2 : 12,56 = 120 (vòng)

c) Bán kính bánh xe B là: 12,56 : (2π) = 12,56 : 6,28 = 2(cm)

Bán kính bánh xe A là: 18,84 : (2π) = 18,84 : 6,28 = 3(cm)

Bài 94

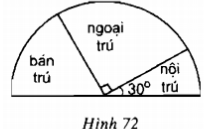
Hãy xem biểu đồ hình quạt biểu diễn sự phân phối học sinh của một trường THCS theo diện ngoại trú, bán trú, nội trú (h.72). Hãy trả lời các câu hỏi sau:

a) Có phải ½ số học sinh là học sinh ngoại trú không ?

b) Có phải 1/3 số học sinh là học sinh bán trú không?

c) Số học sinh nội trú chiếm bao nhiêu phần trăm?

d) Tính số học sinh mỗi loại, biết tổng số học sinh là 1800 em.

Gợi ý đáp án:

Theo cách biểu diễn sự phân phối học sinh như biểu đồ thì:

$\widehat {{O_1}} = {30^0};\widehat {{O_2}} = {90^0};\widehat {{O_3}} = {60^0};\widehat {{AOB}} = {180^0}$

a) Đúng

Vì: $\widehat {{O_2}} = {90^0} = \dfrac{1}{2}\widehat {AOB}$

b) Đúng vì:

$\widehat {{O_3}} = {60^0} = \dfrac{1}{3}\widehat {AOB}$

c) Số học sinh nội trú chiếm : $\dfrac{{30}}{{180}}.100 = 16,7\%$

d) Gọi x, y, z lần lượt là số học sinh nội trú, bán trú, ngoại trú: Ta có:

Số học sinh ngoại trú là $z=\dfrac{1}{2}.1800 = 900$ em

Số học sinh bán trú là $y=\dfrac{1}{3}.1800 = 600$ em

Số học sinh nội trú là x=1800-900-600 = 300 em

Bài 95

Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90^o) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng:

a) CD = CE ; b) ΔBHD cân ; c) CD = CH.

Gợi ý đáp án:

a) Gọi K là giao điểm của BC và AD

Gọi I là giao điểm của BE và AC

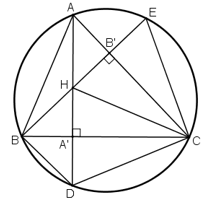
Cách 1:

Ta có: $\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}B} (1)$ (2 góc nội tiếp cùng chắn cung AB)

$\widehat {DBC} + \widehat {ADB} = {90^0}$ (2) (do tam giác BDK vuông tại K)

$\widehat {AEB} + \widehat {CAE} = {90^0}$ (3) (do tam giác AIE vuông tại I)

Từ (1), (2), (3) $\Rightarrow \widehat {CB{\rm{D}}} = \widehat {CA{\rm{E}}}$ (cùng phụ với hai góc bằng nhau)

Có $\widehat {CBD}$ là góc nội tiếp chắn cung CD

$\widehat {EAC}$ là góc nội tiếp chắn cung CE

$⇒ sđ\overparen{CD}= sđ\overparen{CE}$

Suy ra CD = CE

Cách 2:

Vì $BC \bot AD$ nên $\widehat{AKB}=90^0$

Lại có $\widehat{AKB}$ là góc có đỉnh bên trong đường tròn chắn cung AB và CD nên

$\widehat{AKC}=\dfrac{sđ\overparen {DC}+sđ \overparen {BA}}{2}=90^0$

Suy ra $sđ\overparen {AB}+sđ \overparen {CD}=180^0$ (1)

Vì $BE \bot AC$ nên $\widehat{AIB}=90^0$

Lại có $\widehat{AIB}$ là góc có đỉnh bên trong đường tròn chắn cung AB và CE nên

$\widehat{AIB}=\dfrac{sđ\overparen {CE}+sđ \overparen {AB}}{2}=90^0$

Suy ra $sđ\overparen {AB}+sđ \overparen {CE}=180^0$ (2)

Từ (1) và (2) suy ra $sđ \overparen {CE}=sđ \overparen {CD}$

Suy ra $\overparen {CE}=\overparen {CD}$ , do đó CE=CD.

b) Ta có $\widehat {EBC} và \widehat {CB{\rm{D}}}$ là góc nội tiếp trong đường tròn O nên :

$\widehat {EBC} = {1 \over 2} sđ\overparen{CE} và \widehat {CB{\rm{D}}} = {1 \over 2}sđ\overparen{CD}$

Mà $sđ\overparen{CD}= sđ\overparen{CE}$

nên $\widehat {EBC} = \widehat {CB{\rm{D}}}$ suy ra BK là phân giác góc HBD.

Lại có BK vuông góc với HD (giả thiết H là trực tâm của tam giác ABC). Suy ra BK vừa là đường cao vừa là đường phân giác của tam giác HBD nên ∆BHD cân tại B

c) Vì ∆BHD cân và BK là đường cao cũng là đường trung trực của HD. Điểm C nằm trên đường trung trực của HD nên CH = CD

Bài 96

Cho tam giác ABC nội tiếp đường tròn (O) và tia phân giác của góc A cắt đường tròn tại M. Vẽ đường cao AH. Chứng minh rằng:

a) OM đi qua trung điểm của dây BC.

b) AM là tia phân giác của góc OAH.

Gợi ý đáp án:

Vẽ hình

a) Vì AM là tia phân giác của $\widehat {BAC}$ nên $\widehat {BAM} = \widehat {MAC}$

Mà $\widehat {BAM}$ và $\widehat {MAC}$ đều là góc nội tiếp của (O) nên

$\overparen{BM}=\overparen{MC}$

⇒ M là điểm chính giữa cung BC

Vậy $OM \bot BC$ và OM đi qua trung điểm của BC

b) Ta có : $OM \bot BC$ và $AH\bot BC$ nên AH//OM

$\Rightarrow \widehat {HAM} = \widehat {AM{\rm{O}}}$ (so le trong) (1)

Mà ∆OAM cân tại O (do OA=OM (= bán kính đường tròn (O)) nên $\widehat {AM{\rm{O}}} = \widehat {MAO} (2)$

Từ (1) và (2) suy ra: $\widehat {HA{\rm{M}}} = \widehat {MAO}$

Vậy AM là đường phân giác của góc OAH

Bài 97

Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:

a) ABCD là một tứ giác nội tiếp;

b) $\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}} ;$

c) CA là tia phân giác của góc SCB

+ Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: Nếu hai đỉnh kề một cạnh của một tứ giác cùng nhìn cạnh đối diện dưới các góc bằng nhau thì tứ giác đó là tứ giác nội tiếp.

Gợi ý đáp án:

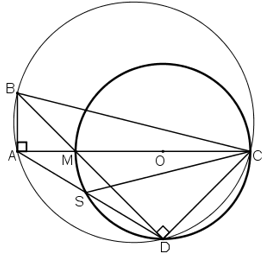a) Ta có góc $\widehat {MDC}$ là góc nội tiếp chắn nửa đường tròn (O) nên $\widehat {MDC} = {90^0}$

⇒ ∆CDB là tam giác vuông nên nội tiếp đường tròn đường kính BC.

Ta có ∆ABC vuông tại A.

Do đó ∆ABC nội tiếp trong đường tròn tâm I đường kính BC.

Ta có A và D là hai đỉnh kề nhau cùng nhìn BC dưới một góc $90^0$ không đổi nên tứ giác ABCD nội tiếp đường tròn đường kính BC

b) Ta có $\widehat {AB{\rm{D}}}$ là góc nội tiếp trong đường tròn (I) chắn cung AD.

Tương tự góc $\widehat {AC{\rm{D}}}$ là góc nội tiếp trong đường tròn (I) chắn cung AD

Vậy $\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}$

c) Ta có:

$\widehat {ADB} + \widehat {BDS} = {180^0}$ ( 2 góc kề bù)

Mà $\widehat {MCS} + \widehat {MDS} = {180^0}$ (tứ giác CMDS nội tiếp đường tròn (O)

Từ đó ta có: $\widehat {ADB}=\widehat {MCS}$ (1)

Lại có tứ giác ABCD nội tiếp nên $\widehat {ADB}=\widehat {ACB}$ (2)

Từ (1) và (2) ta suy ra $\widehat {MCS}=\widehat {ACB}$

Vậy tia CA là tia phân giác của góc SCB

Bài 98

Cho đường tròn (O) và một điểm A cố định trên đường tròn. Tìm quỹ tích các trung điểm M của dây AB khi điểm B di động trên đường tròn đó.

Hướng dẫn giải

- Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

Gợi ý đáp án:

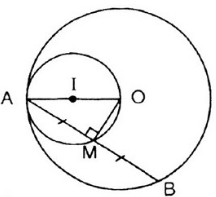
+) Phần thuận: Giả sử M là trung điểm của dây AB. Do đó, $OM \bot AB$ hay $\widehat {AMO} = 90^\circ .$ Khi B di động trên đường tròn (O) điểm M luôn nhìn đoạn OA cố định dưới một góc vuông. Vậy quỹ tích của điểm M là đường tròn tâm I đường kính OA.

+) Phần đảo: Lấy điểm M’ bất kì trên đường tròn (I). Nối M’ với A, đường thẳng M’A cắt đường tròn (O) tại B’. Nối M’ với O, ta có $\widehat {AM'O} = {90^0}$ hay $OM’ \bot AB’$

⇒ M là trung điểm của AB’

Kết luận: Tập hợp các trung điểm M của dây AB là đường tròn đường kính OA.

Bài 99

Dựng ΔABC, biết BC = 6cm, $\widehat {BAC} = 80^\circ$ , đường cao AH có độ dài là 2cm.

Gợi ý đáp án:

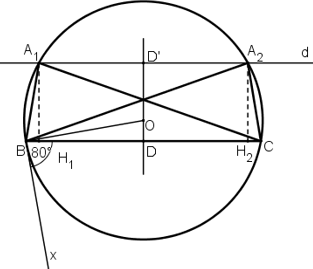
Cách dựng:

+ Dựng đoạn thẳng BC = 6cm.

+ Dựng cung chứa góc 80º trên đoạn thẳng BC (tương tự bài 46) :

Dựng tia Bx sao cho $\widehat {CBx} = 80^\circ$

Dựng tia By ⊥ Bx.

Dựng đường trung trực của BC cắt By tại O.

Dựng đường tròn (O; OB).

Cung lớn BC chính là cung chứa góc 80⁰ dựng trên đoạn BC.

+ Dựng đường thẳng d song song với BC và cách BC một đoạn 2cm:

Lấy D là trung điểm BC.

Trên đường trung trực của BC lấy D’ sao cho DD’ = 2cm.

Dựng đường thẳng d đi qua D’ và vuông góc với DD’.

+ Đường thẳng d cắt cung lớn BC tại A.

Ta được ΔABC cần dựng.

Chứng minh:

+ Theo cách dựng có BC = 6cm.

+ A ∈ cung chứa góc 80^o dựng trên đoạn BC

$\widehat {BAC} = 80^\circ$

+ A ∈ d song song với BC và cách BC 2cm

⇒ AH = DD’ = 2cm.

Vậy ΔABC thỏa mãn yêu cầu đề bài.

Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.

Giải Toán 9 trang 103, 104, 105 - SGK Toán 9 Tập 2

Giải Toán 9: Ôn tập Chương III

Giải SGK Toán 9 Hình học Tập 2 (trang 103, 104, 105)

Giải Toán 9: Ôn tập Chương III: Góc với đường tròn

Giải Toán 9 trang 103, 104, 105 tập 2

Bài 88

Bài 89

Bài 90

Bài 91

Bài 92

Bài 93

Bài 94

Bài 95

Bài 96

Bài 97

Bài 98

Bài 99

Liên kết tải về

Chủ đề liên quan

Học tập

Lớp 9

Giải Toán 9

Chia sẻ

Có thể bạn quan tâm

Được tải nhiều nhất

Bài viết mới nhất